B 8672-1:2011
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 記号及び単位 ··················································································································· 3
5 信頼度の決定方法 ············································································································· 3
6 試験の実施方法 ················································································································ 4
7 統計的解析 ······················································································································ 4
8 試験条件························································································································· 4
9 標本の大きさ及び選択基準 ································································································· 5
10 試験の終了 ···················································································································· 6
11 試験データによる信頼度の評価 ························································································· 6
12 試験報告書 ···················································································································· 8
13 規格準拠表示 ················································································································· 8
附属書A(参考)中途打切りを含まない打切りデータの計算方法··················································· 9
附属書B(参考)中途打切りを含む打切りデータの計算方法 ························································ 13
附属書C(参考)指定の信頼度に対する寿命の実証試験 ····························································· 18
附属書D(参考)試験データにおける異常値の取扱い ································································ 21
附属書JA(参考)ワイブル解析のための数学的補遺 ·································································· 25
附属書JB(参考)JISと対応国際規格との対比表 ······································································ 33
B 8672-1:2011
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本フルードパワー工業会(JFPA)
及び財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があ
り,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 8672(空気圧−試験による機器の信頼性評価)の規格群には,次に示す部編成がある。
JIS B 8672-1 第1部:通則
JIS B 8672-2 第2部:方向制御弁(予定)
JIS B 8672-4 第4部:減圧弁
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 8672-1:2011
空気圧−試験による機器の信頼性評価−
第1部:通則
Pneumatic fluid power-Assessment of component reliability by testing-
Part 1: General procedures
序文
この規格は,2007年に第1版として発行されたISO 19973-1を基とし,技術的内容を変更して作成した
日本工業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JBに示す。また,附属書JAは対応国際規格にはない事項であ
る。
1
適用範囲
この規格は,空気圧機器の信頼度を試験によって決定するための一般的な手順,結果の解析方法,報告
方法,一般的な試験条件及びデータの評価方法について規定する。これらは,機器の種類及びそれらの設
計とは無関係である。ここで規定する方法は,未修理の機器が初回故障に至るまでの寿命に適用する。
なお,異常値は除外するが,異常値は重要な意味をもつこともあるため,その取扱いに関する情報を,
附属書Dに示す。
注記1 この規格は,主として一定の故障確率(10 %)に注目して機器の信頼度を評価するものであ
るが,そのため設計及び構造が非常に異なり,故障モードが異なる製品の比較には注意を要
する。故障モードが異なる,又は故障の確率分布が大きく異なる製品間では,設定する故障
確率の値で優劣が逆転することもあり得るからである。そのような場合には,各製品の母集
団について推定される確率分布に基づいて判断する必要があるが,それはこの規格の範囲外
である。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 19973-1:2007,Pneumatic fluid power−Assessment of component reliability by testing−Part 1:
General procedures(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
2
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 0142 油圧・空気圧システム及び機器−用語
注記 対応国際規格:ISO 5598,Fluid power systems and components−Vocabulary(MOD)
JIS B 8392-1 圧縮空気−第1部:汚染物質及び清浄等級
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability(MOD)
JIS Z 8115 ディペンダビリティ(信頼性)用語
注記 対応国際規格:IEC 60050-191,International Electrotechnical Vocabulary. Chapter 191:
Dependability and quality of service(MOD)
JIS Z 8203 国際単位系(SI)及びその使い方
注記 対応国際規格:ISO 1000,SI units and recommendations for the use of their multiples and of certain
other units(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0142,JIS Z 8101-1及びJIS Z 8115によるほか,次による。
3.1
信頼度(reliability)
製品が所定の条件下で所定の期間,所定の機能を果たすことができる確率(JIS Z 8115参照)。
注記 一般には信頼性(reliability)という用語も用いられるが,それは導電性,耐水性などのように
特定性質の分野を表すもので,信頼性の度合いを示すのが信頼度である。
3.2
故障(failure)
製品が要求された機能を果たす能力を失うこと(JIS Z 8115参照)。ただし,この規格(全ての部を含む。)
では,機器の特性がしきい値に達することも故障とみなす。
3.3
完全故障(catastrophic failure)
対象とする製品に要求される全ての機能が,完全に働かなくなる故障(JIS Z 8115参照)。
3.4
該当故障(relevant failure)
信頼度の評価で対象とする故障(JIS Z 8115参照)。
3.5
故障寿命(time to failure)
製品が故障に至るまでの寿命(JIS Z 8115参照)。
なお,この規格(全ての部を含む。)では,寿命1)サイクル数又は距離のいずれかで表現する。
注1) 一般には寿命時間ともいい,記号tで表す。
3.6
しきい値(threshold level)
機器の性能特性(漏れ,切替圧力,ストローク時間など)が,試験によって劣化したかどうかを判定す
るための臨界値2)。
注2) 性能比較の臨界値として専門家が決めた任意の値であり,必ずしも機器の実際の故障を表すも

3
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
のとは限らない。
3.7
標本(sample)
母集団の性質を把握するために,母集団から無作為に抜き取った1個以上の試験に供する製品(JIS Z
8101-1参照)。
3.8
標本の大きさ(sample size)
標本に含まれる個別の製品の数3)(JIS Z 8101-1参照)。
注3) 多段階サンプリングでは,標本の大きさはサンプリングの最終段階での個別の製品の合計数と
なる。
3.9
信頼限界(confidence limit)
母集団の分布を決定している定数を標本から推定したとき,その真値が所定の確率で含まれている区間
を表す上下限値(JIS Z 8101-1参照)。
3.10
片側信頼区間(one-sided confidence interval)
信頼限界の一方だけを定めた区間で,例えば寿命時間については下限値だけを定め,上限値を無限大と
した区間(JIS Z 8101-1参照)。
3.11
信頼水準(confidence level),信頼係数(confidence coefficient)
推定値の真値が信頼区間に含まれる確率(JIS Z 8101-1参照)。
4
記号及び単位
4.1
記号及び定義
この規格で用いる記号及び定義は,表1による。
表1−記号及び定義
記号
定義
B10
母集団の故障確率が10 %に到達する寿命時間
η
ワイブル分布の尺度母数(特性寿命)
β
ワイブル分布の形状母数(ワイブル係数)
F(t)
故障確率
R(t)
信頼度 R(t)=1−F(t)
t
一般に寿命時間(この規格ではサイクル数又は距離)
4.2
単位
この規格で用いる単位は,JIS Z 8203による。
5
信頼度の決定方法
この規格(全ての部を含む。)において,信頼度とは,所定の条件で機器を作動させたとき,所定の寿命
時間まで,該当故障が起こらない確率を指す。
4
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで該当故障とは,機器が次の状態に至った場合をいう。
− 所定の特性パラメータの値が,所定のしきい値を超えた場合。
− 完全故障(破裂,疲労,機能故障など)が起こった場合。
この規格が対象とする機器の作動条件,特性パラメータ及びそのしきい値は,対応する各部で規定して
いる。信頼度は,試験結果から母集団の寿命分布を推定することによって決定する。寿命分布を表すため,
一般には種々の異なる分布関数が用いられている。
なお,母集団の寿命分布がほぼ分かっているときは,数個の製品からなる標本について,所要の寿命よ
り長めの試験を行うことによって,機器の信頼度を実証することができる。具体的な方法については,附
属書Cに示す。
6
試験の実施方法
6.1
加速寿命試験
信頼性試験を実施する際の大きな問題点の一つに,しきい値に到達するまでの試験時間の長さが挙げら
れる。試験時間を妥当な長さにするためには,機器を定格値よりも過酷な環境条件にさらす加速試験が必
要となる場合がある。試験の加速係数の決定に当たっては,故障モード又は故障メカニズムが変化しない
か,又はそれらが加速しないときの試験から予測されるものと異ならないことが条件である。
6.2
試験装置及び特性パラメータの測定
二つの重要な要素として,試験装置及び機器の特性パラメータの測定がある。試験装置は,計画された
環境条件で確実に動作するよう設計する必要がある。その構造などによって,試験結果に影響があっては
ならない。試験装置の評価及び試験期間中の保守は重要である。正確,かつ,再現性のある試験結果を得
るためには,特性パラメータの測定精度及び試験中のパラメータの監視精度は,指定された公差内でなけ
ればならない。
6.3
試験計画
指定された条件で,機器の信頼度を的確に評価した結果を得るためには,適切な試験計画を立てること
が望ましい。製造業者と使用者とがこの規格(全ての部を含む。)を適用することに同意した場合は,試験
計画の目標及び目的を明確に定めなければならない。
7
統計的解析
信頼度を評価するためには,得られた試験データを用いて母集団の寿命分布の母数を推定する必要があ
る。そのとき,最も一般的に用いられる方法の一つとしてワイブル解析がある。この規格では,試験結果
の比較を可能にするため,信頼性データの解析は,ワイブル解析によるものとする4)。
ワイブル解析の実施例を附属書A及び附属書Bに,また,数学的な基礎について附属書JAにそれぞれ
示す。
注4) 実施に当たっては市販品を含む適切なソフトウェアを使用することができる。
8
試験条件
8.1
一般事項
試験は,対象とする特性パラメータ,各特性パラメータに対するしきい値などに関し,この規格の各部
で機器ごとに規定した内容に準拠して行わなければならない。
5
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2
試験中における標本の修理
信頼性試験中は,標本の修理(部品の交換,再組み付けなど)は行ってはならない。
8.3
試験環境
この規格の各箇条で指定されている場合,又は製造業者と使用者との間で合意した場合を除き,全ての
試験は表2の環境条件において実施しなければならない。
表2−一般の試験環境条件
パラメータ
値
使用圧力
630±30 kPa
周囲温度
23±10 ℃
媒体温度
23±10 ℃
空気の品質
公称ろ過度
5 µm
最高圧力露点a)
−20〜+7 ℃
油分
なし
注a) ISO規格では+3 ℃としているが,JIS B 8392-1
に従って,−20〜+7 ℃と規定する。
8.4
特性パラメータの測定
信頼性試験に先立ち,試験実施担当者は予想される寿命に応じて,特性パラメータの測定間隔を決定し
なければならない。効果的な測定間隔の決定は,試験担当者の経験及び適切な判断によるところが大きい。
測定間隔が空きすぎると,統計的に判定される寿命が短くなる可能性がある(10.2参照)。逆に測定間隔が
短すぎると,試験コストが高くなる。
試験状態が安定するまでの試験立上げ時は,頻繁に測定を実施するのがよい。初回の測定は,予想寿命
の10 %以内で実施しなければならない。測定装置は継続して稼働させ,適切に機能していることを定期的
に確認しなければならない。
注記 測定装置は,特性パラメータを常時監視し,故障の時点を的確に判定できるものが望ましい
(10.2参照)。
9
標本の大きさ及び選択基準
9.1
一般事項
標本は,母集団を代表するように,無作為に選ばなければならない。
9.2
標本の大きさ
標本の大きさは,7個以上とする。
注記 ワイブル確率紙上の最初のデータポイントが,10 %未満の故障確率になるために,標本は少な
くとも7個あることが重要である。これによって,10 %の故障確率に対する片側信頼限界をよ
り正確に推定でき,B10寿命を精度よく決定することができる(JA.2.2参照)。
9.3
標本の選択基準
設計原理が同じ製品シリーズでは,全ての形式又はサイズの製品を試験する必要はない。ただし,試験
対象品には,例えば,最高速度など,最も厳しい条件の形式が含まれていなければならない。
6
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10 試験の終了
10.1 要求最小故障数
表3に,B10寿命を適切に評価するために要求される最小故障数を示す。この数字には,故障とみなされ
ない停止は含めない。試験は,要求最小故障数を満たすまで,継続して行わなければならない。
表3−B10寿命を評価するための要求最小故障数
標本の大きさ
7
8
9
10
11以上
要求最小故障数
5
6
7
7
標本の大きさの70 % ,端数切り捨てa)
注a) 例えば,標本の大きさが11の場合,要求最小故障数は7である。
10.2 寿命サイクル数
試験中に,ある標本が特性パラメータの測定間隔の間で故障したときは,左側打切りデータとみなす。
この場合は,その標本が正常に動作していたときの寿命時間及び故障を発見したときの寿命時間の両方を
記録する。
故障寿命をより正確に決定することが要求される場合は,リミットスイッチ又は故障を検知するための
適切な他の方法を用いて,個別の標本の性能を継続的にモニターすることが必要である。
注記 左側打切りデータとは,最後に正常に動作していたときの寿命で試験を打ち切ったとみなすこ
とである。
なお,最ゆう(尤)推定法(以下,最ゆう推定法という。)などを用いて,故障発見寿命と直
前の正常作動寿命との間に真の寿命があるとして解析することもできる(附属書A及び附属書
B参照)。
10.3 中途打切り試験
該当故障が起こる前に,個別の標本の試験を中止することがある。これは,中途打切りと呼ばれている。
中途打切りの例を,次に示す。
− その標本を検査のために分解し,試験の継続ができなくなったとき。
− その標本を誤って損傷し,試験の継続ができなくなったとき。
これらの標本は中途打切りまでにある程度の寿命試験に耐えており,そのデータは信頼度の計算にプラ
スの影響を与えるため無視してはならない。中途打切りを含むデータの解析は,附属書Bを参考にして行
うのがよい。
10.4 打切り試験
表3に規定した要求最小故障数に達した後も,依然,残りの標本が正常に作動している場合,それらの
試験は打ち切ることができる。
中途打切りを含まない打切り試験の場合は,附属書Aに示す方法を用いて解析を行う。1個以上の中途
打切りを含む打切り試験の場合は,附属書Bに示す方法を用いて解析を行う。
注記 一般に,あらかじめ定めた最大寿命時間において,試験を打ち切ることが多い。
11 試験データによる信頼度の評価
11.1 故障モード
試験結果を的確に評価するため,あらかじめ対象とする故障モード(複数でもよい)を定めておき,個
別の標本ごとに故障モードを記録しなければならない。
7
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11.2 母数推定
試験データを用いて,次に示す母数を計算し決定する。
− 尺度母数η:ワイブル確率紙上の直線が故障確率63.2 %の線を切る寿命値。
− 形状母数β:ワイブル確率紙上の直線の傾き。
注記 この規格の対応国際規格ISO 19973-1では,母数を求める計算方法,及びワイブル確率紙上に
直線を描く方法は特に規定せず,市販のソフトウェアを利用してよいとしている。最も一般的
に用いられる方法はメディアンランク回帰法で,中途打切りデータ及び左側打切りデータにつ
いては最ゆう推定法を用いることもできる。これらの方法の適用例は附属書A及び附属書Bに
示してあるが,更に数学的な基礎について附属書JAに示す。
11.3 B10寿命
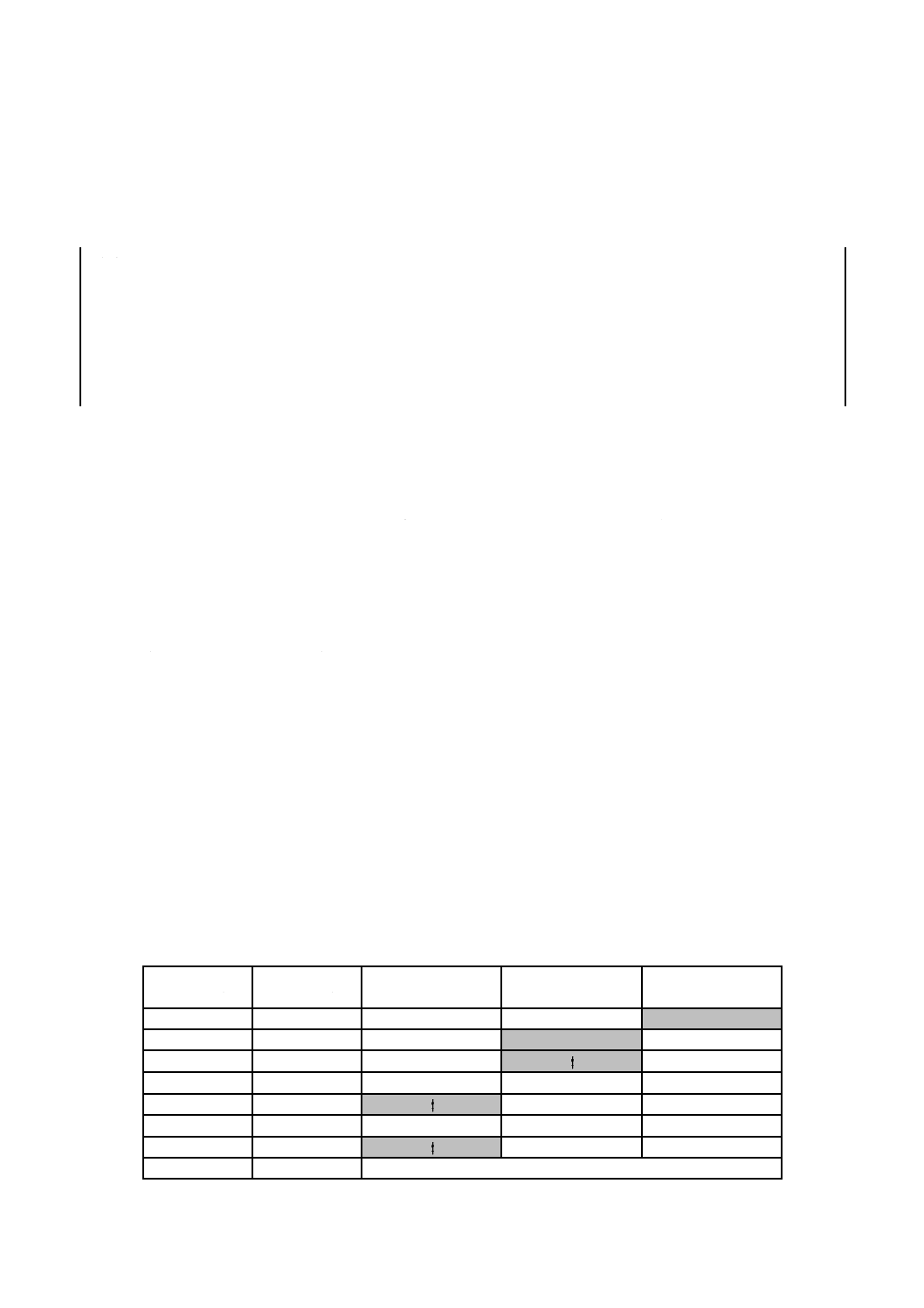
11.2で推定した母数を用いてB10寿命を計算する(図1のbを参照)。
11.4 B10寿命の信頼限界
フィッシャーのマトリックス法(附属書JA)によって,信頼水準95 %におけるB10寿命の信頼限界を計
算する(図1のaを参照)。
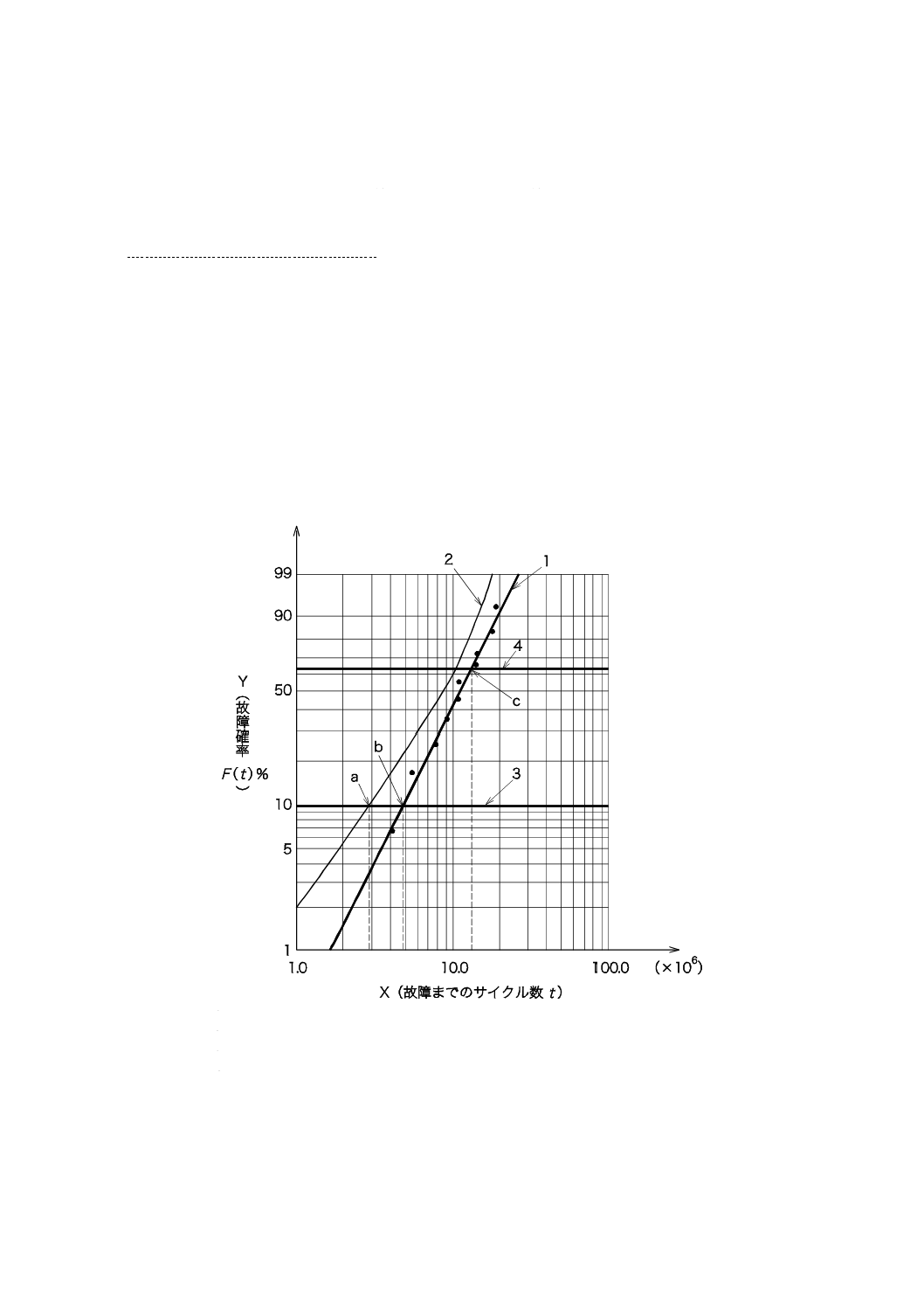
1
最適当てはめ線
2
フィッシャーのマトリックス法による95 %信頼限界
3
故障確率F(t)=10 %の線
4
故障確率F(t)=63.2 %の線
a
信頼水準95 %におけるB10寿命の信頼限界
b
B10寿命
c
特性寿命η
図1−B10寿命の決定例
8
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
12 試験報告書
試験報告書には,少なくとも次の事項を記載しなければならない。
a) JIS B 8672及び該当機器に対応する部の番号
b) 試験報告年月日
c) 機器の種類(製作者,形式,シリーズ番号)
d) 標本の大きさ
e) 試験条件(使用圧力,温度,空気の質,周波数,負荷など)
f)
故障の判定に用いた特性パラメータ及びそのしきい値
g) 個別の標本ごとの故障モード及び故障寿命
h) 解析対象とした故障数
i)
特性寿命η及びワイブル係数β
j) B10寿命及び信頼水準95 %におけるB10寿命の信頼限界
k) i)及びj)を推定するためのグラフ(図1の直線1及び曲線2)
l)
ワイブル関数の当てはめなど主な計算方法(例えば,メディアンランク回帰法,最ゆう推定法,フィ
ッシャーのマトリックス法)
m) 異常値の有無及びその詳細,また,必要に応じ他の特記事項
13 規格準拠表示
この規格に準拠して信頼性評価を行った製造業者に対し,試験報告,カタログ及び販売資料作成時に,
次の内容を盛り込むよう強く推奨する。
“試験による空気圧機器の信頼性を評価するための一般手順は,“JIS B 8672-1,空気圧−試験による機
器の信頼性評価−第1部:通則”に準拠して実施した。”
9
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
中途打切りを含まない打切りデータの計算方法
A.1 概要
この附属書では,中途打切りデータ(10.3参照)を含まない打切りデータ(10.4参照)の計算方法につ
いて,最ゆう推定法及びメディアンランク回帰法を用いた計算例を示す。また,これらの方法の説明及び
詳しい解析のための数学的補遺は,附属書JAに示す。
なお,試験の打切りを行わず,標本全てを故障まで試験したときも,解析対象となるデータが増えるだ
けで,解析方法は全く同じである。
A.2 最ゆう推定法の適用例
A.2.1 対象とするデータ
大きさが7個の標本について信頼性試験中に,3種類の故障モード(1,2,3)に関連した特性パラメー
タを測定したとする。各特性パラメータのデータは試験の進行に従って監視し,個別の標本が要求された
機能を果たすことができなくなった場合,又は特性パラメータの値がしきい値に達した場合のいずれかを
故障と判定する(3.4参照)。
最ゆう推定法では,特性パラメータを間欠的に測定している場合に,個別の標本の故障を最初に発見し
たとき,及びその直前に正常な作動を確認していたときの両方の寿命時間を用いて解析を行う。この場合,
故障寿命は,計測した二つの寿命時間の間のどこかにある。
表A.1は,寿命時間としてサイクル数を用いた例で,故障モード別にみた二つのサイクル数データ(最
終正常稼働サイクル数及び故障発見サイクル数)と個別の標本との関係を,サイクル数の順に整理したも
のである。この例では,標本5の故障モード3による故障が最も早く起こり,その寿命は,10.8×106サイ
クルと12.8×106サイクルとの間にある。個別の標本についての最初の故障及びそのモードは,灰色の欄に
示す。全体の試験は,表3で規定された要求最小故障数に達したとき打ち切ることができる。この例では
要求最小故障数5であり,試験の打切りサイクル数は44.9×106としている。
なお,特性パラメータがしきい値に達し故障と判定された標本についても,試験を継続することはでき
る。この例では標本5,1,2がそれである。ただし,一旦故障が記録された標本のそれ以降の故障データ
は信頼性解析には考慮しない。
表A.1−間欠測定の場合のデータ例(最ゆう推定法を適用)
最終正常稼働
サイクル数
故障発見
サイクル数
故障モード1
例:シールAの漏れ
故障モード2
例:シールBの漏れ
故障モード3
例:切換時間
10.8×106
12.8×106
−
−
標本5
19.5×106
23.5×106
−
標本1
−
28.2×106
32.2×106
−
標本2
−
34.2×106
36.6×106
標本2
標本5
−
37.8×106
41.8×106
標本3
−
標本1
42.9×106
43.9×106
標本5
−
−
44.9×106
44.9×106
標本6
−
−
44.9×106
−
標本4及び標本7は該当故障がないまま試験打切り
10
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.2.2 解析結果
図A.1に,解析結果を示す。解析した寿命データは,表A.1の最終正常稼働サイクル数及び故障発見サ
イクル数の両方で,図中にその範囲を線分で,中央値(この場合は平均値)を黒点で示してある。プロッ
トに当てはめた直線及び対応する母数は最ゆう推定法から求めており,信頼限界はその母数を用いフィッ
シャーのマトリックス法に基づいて求めている。
A.2.3 母数の推定値
− 尺度母数(特性寿命):η=42.4×106サイクル
− 形状母数(ワイブル係数):β=2.38
A.2.4 B10寿命の推定値
ワイブル分布関数の両辺の対数を2回とり変形すると,式(A.1)が得られる。
β
η
1
)
(
1
1
ln
ln
−
=
t
F
t
································································ (A.1)
B10はF(t)=0.1における寿命であるから,式(A.1)にこれを代入すると,推定した母数に対し次のように
なる。
B10=16.5×106サイクル
A.2.5 B10寿命の信頼限界
95 %信頼水準におけるB10寿命の信頼限界は,フィッシャーのマトリックス法(附属書JA参照)による
と,8.42×106サイクルである。
A.3 メディアンランク回帰法の適用例
A.3.1 対象とするデータ
メディアンランク回帰法は,故障寿命が範囲ではなく数値として確定している場合に適用する。通常こ
のためには,特性パラメータを連続測定する装置を用いるなどによって,故障の起こった寿命時間を直接
示すことができるようにする必要がある。
この例で使用するデータは,寿命サイクル数ti及び標本の大きさ7に対するメディアンランクpiととも
に表A.2に示す。
なお,表3から,この場合の要求最小故障数は5であるので,試験はデータが5個得られた時点の44.9
×106サイクルで打切りとしている。
表A.2−連続測定の場合の寿命データ例(メディアンランク回帰法を適用)
順位i
寿命サイクル数ti
メディアンランクpi
1
11.8×106
0.095
2
21.5×106
0.230
3
30.2×106
0.365
4
39.8×106
0.500
5
44.9×106
0.635
6,7
44.9×106超
−
注記 10.2では,故障寿命は最後に正常稼働を確認したサイクル数とすることを規定している。この
例では表A.1のデータを借用し,最終正常稼働サイクル数と故障発見サイクル数との中央値を
11
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
用いているが,それはあくまで最ゆう推定法との比較のためにとった便法である。
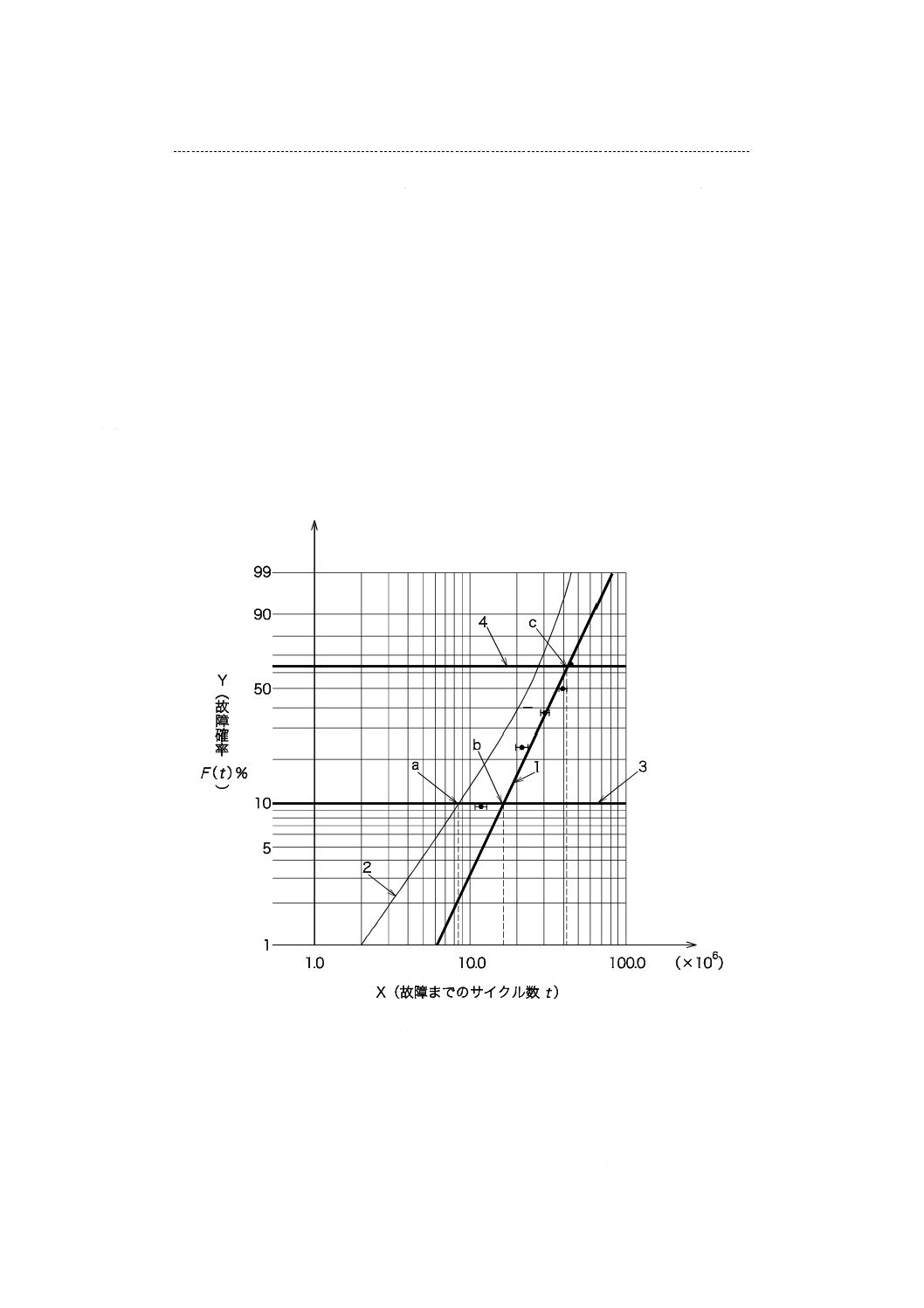
A.3.2 解析結果
図A.2に,解析結果を示す。故障寿命のデータ点は,図A.1の黒点と同じである。データに当てはめた
直線はメディアンランク回帰法によるもので,それに基づきワイブル分布の母数を求めている。また,信
頼限界は,フィッシャーのマトリックス法に基づいて求めたものである。
A.3.3 母数の推定値
− 尺度母数(特性寿命):η=46.2×106サイクル
− 形状母数(ワイブル係数):β=1.74
A.3.4 B10寿命の推定値
A.2.4と同様に,式(A.1)でF(t)=0.1とおくと,推定した母数に対し次のようになる。
B10=12.7×106サイクル
A.3.5 B10寿命の信頼限界
95 %信頼水準におけるB10寿命の信頼限界は,フィッシャーのマトリックス法から,次の値となる。
6.35×106サイクル
1
最ゆう推定法による直線
2
フィッシャーのマトリックス法による95 %信頼限界
3
故障確率F(t)=10 %の線
4
故障確率F(t)=63.2 %の線
a
信頼水準95 %におけるB10寿命の信頼限界
b
B10寿命
c
特性寿命η,この場合42.4×106サイクル
図A.1−最ゆう推定法による解析例(表A.1のデータ)
12
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
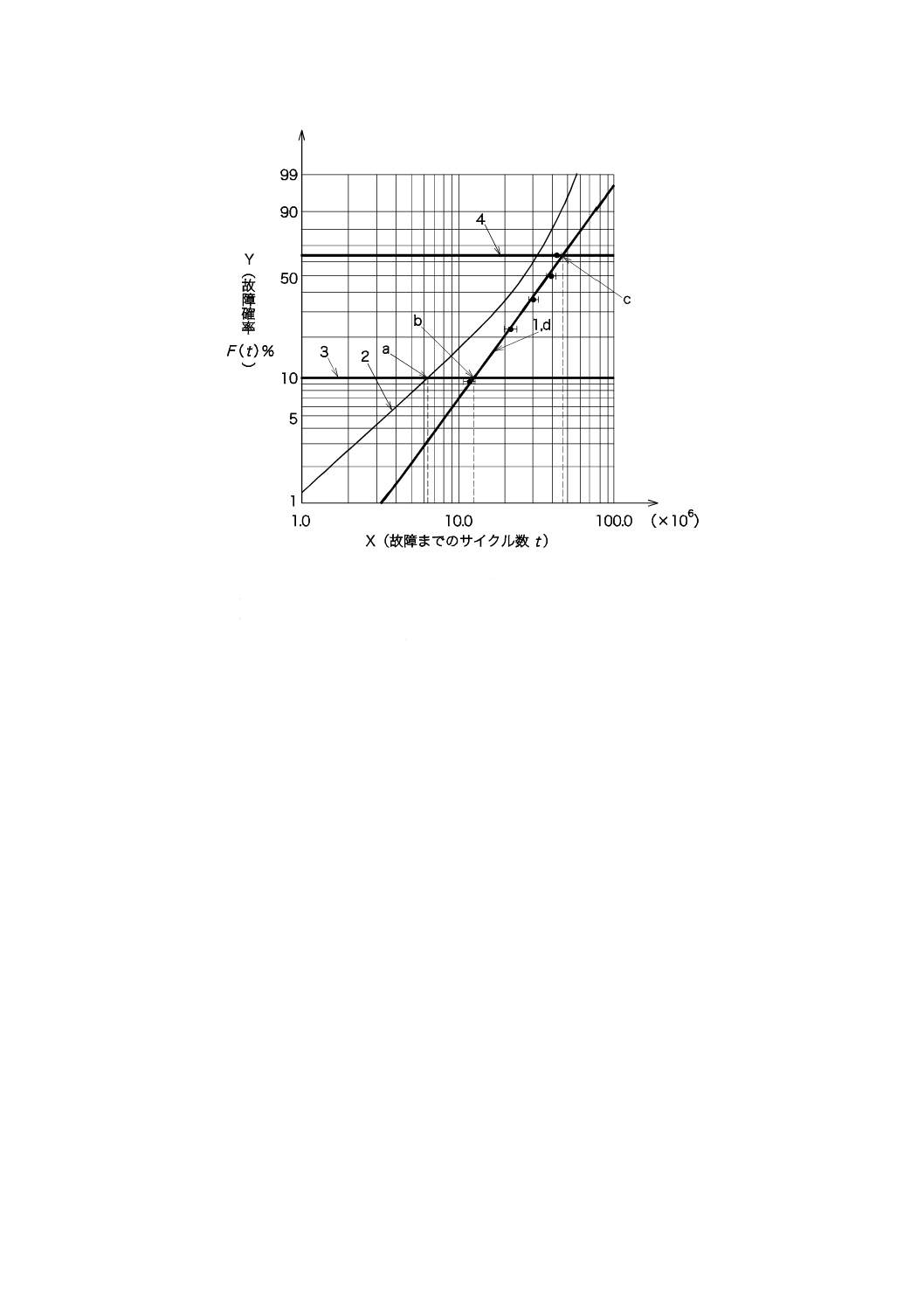
1
メディアンランク回帰法による直線
2
フィッシャーのマトリックス法による95 %信頼限界
3
故障確率F(t)=10 %の線
4
故障確率F(t)=63.2 %の線
a
信頼水準95 %におけるB10寿命の信頼限界
b
B10寿命
c
特性寿命η,この場合46.2×106サイクル
d
ワイブル係数βは1.74
図A.2−メディアンランク回帰法による解析例(表A.2のデータ)
13
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
中途打切りを含む打切りデータの計算方法
B.1
概要
この附属書では,中途打切りデータ(10.3参照)を含む打切りデータ(10.4参照)の計算方法について,
最ゆう推定法及びメディアンランク回帰法を用いた計算例を示す。また,これらの方法の説明及び詳しい
解析のための数学的補遺は,附属書JAに示す。
なお,試験の打切りを行わず,中途打切り以外の全ての標本を故障まで試験したときも,解析対象とな
るデータが増えるだけで,解析方法は全く同じである。
B.2
最ゆう推定法の適用例
B.2.1 対象とするデータ
試験のため抜き取った12個の製品からなる標本について,3種類の故障モード(1,2,3)に関する特
性パラメータを測定したとする。各特性パラメータの値は試験の進行に従って測定し,個別の標本が要求
された機能を果たすことができなくなった場合,又は特性パラメータの値がしきい値に達した場合のいず
れかを故障と判定する(3.4参照)。
最ゆう推定法では,特性パラメータを間欠的に測定している場合に,故障が最初に発見されたときの寿
命時間及びその直前に正常な作動を確認したときの寿命時間の両方を用いて解析を行う。この場合,故障
寿命は,計測した二つの寿命時間の間のどこかにある。
表B.1は,寿命時間としてサイクル数を用いた例で,故障モード別にみた最終正常稼働サイクル数及び
故障発見サイクル数を個別の標本について,サイクル数の順に整理したものである。この例では,故障モ
ード3による標本5の故障が最も早く起こり,その寿命は,表の1行目に示すように2.5×106サイクルと
3.2×106サイクルとの間にある。個別の標本に関する最初の故障及びそのモードは,灰色の欄に示す。全
体の試験は,表3で規定された要求最小故障数に達したとき打ち切ることができる。この例では要求最小
故障数は8であるが,試験は55.9×106サイクルまで行い,9個のデータを得ている。
なお,標本4及び標本10は,検査のため中途で試験を打ち切っている。また,特性パラメータがしきい
値に達し故障と判定された標本5及び標本2についても,試験を継続している。ただし,一旦故障が記録
された以降の故障データは,信頼性解析には考慮していない。解析に用いるのは灰色の欄に関する二つの
サイクル数だけで,合計18個である。
14
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
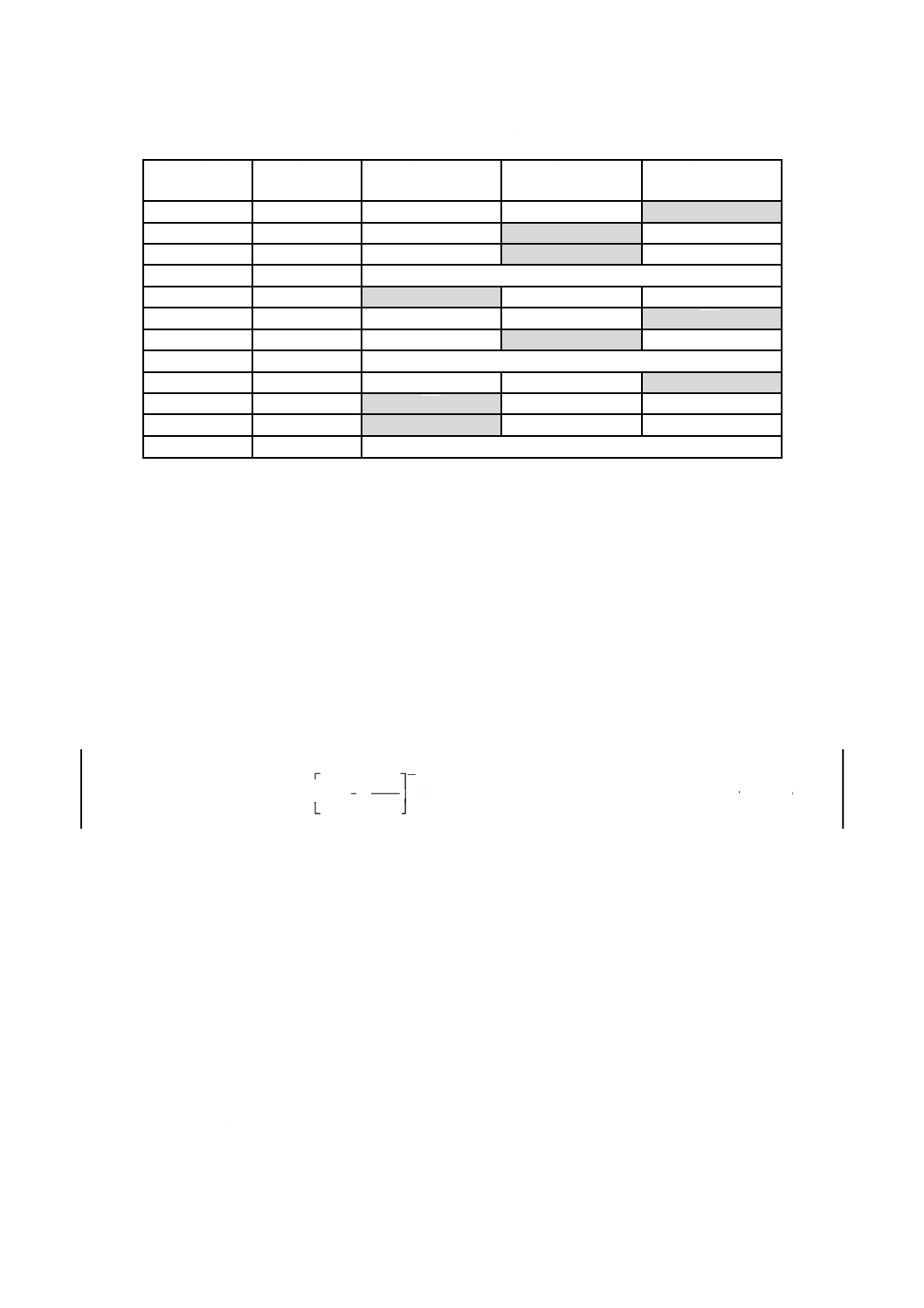
表B.1−中途打切りを含む間欠測定の場合のデータ例(最ゆう推定法を適用)
最終正常稼働
サイクル数
故障発見
サイクル数
故障モード1
例:シールAの漏れ
故障モード2
例:シールBの漏れ
故障モード3
例:切換時間
2.5×106
3.2×106
−
−
標本5
4.8×106
6.2×106
−
標本12
−
10.5×106
12.5×106
−
標本1
−
15.0×106
詳細検査のため,標本4は試験から除く
16.0×106
18.0×106
標本9
−
−
21.2×106
24.2×106
−
−
標本2
29.6×106
33.6×106
標本2
標本8
35.0×106
故障を検査するため,標本10は試験から除く
37.8×106
40.8×106
−
−
標本3
40.8×106
44.1×106
標本11
標本5
−
48.9×106
55.9×106
標本6
−
標本1
55.9×106
試験の打切り−標本7は該当故障なし
B.2.2 解析結果
図B.1に,解析結果を示す。解析した寿命データは,表B.1の最終正常稼働サイクル数及び故障発見サ
イクル数の両方で,図中にその範囲を線分で,中央値(この場合は平均値)を黒点で示してある。プロッ
トに当てはめた直線及び対応する母数は最ゆう推定法から求めており,信頼限界はその母数を用いフィッ
シャーのマトリックス法に基づいて求めている。
B.2.3 母数の推定値
− 尺度母数(特性寿命):η=36.5×106サイクル
− 形状母数(ワイブル係数):β=1.36
B.2.4 B10寿命の推定値
ワイブル分布関数の両辺の対数を2回とり変形すると,式(B.1)が得られる。
β
η
1
)
(
1
1
ln
ln
−
=
t
F
t
································································ (B.1)
B10はF(t)=0.1における寿命であるから,式(B.1)にこれを代入すると,推定した母数に対し次のように
なる。
B10=6.98×106サイクル
B.2.5 B10寿命の信頼限界
95 %信頼水準におけるB10寿命の信頼限界は,フィッシャーのマトリックス法(附属書JA参照)による
と,2.9×106サイクルである。
B.3
メディアンランク回帰法の適用例
B.3.1 対象とするデータ
メディアンランク回帰法は,故障寿命が確定している場合に適用する。通常は,特性パラメータの測定
装置が故障の起こった寿命時間を直接示すことができるようにしておく。ここでは最ゆう推定法との比較
のため,表B.1のデータをそのまま借用し,最終正常稼働サイクル数と故障発見サイクル数との平均値を,
仮に寿命サイクル数とみなして解析する。

15
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この例で使用する寿命サイクル数は,標本の大きさ12に対する中途打切りを含むデータのメディアンラ
ンク(B.3.3参照)とともに表B.2に示す。
なお,表3から,この場合の要求最小故障数は8であるが,試験は55.9×106サイクルで打切りとしたの
で,故障データは9個となっている。
注記 表B.1のデータは特性パラメータの間欠測定に基づいているが,10.2ではそのような場合,故
障寿命は最後に正常稼働を確認したサイクル数とすることを規定している。この例で故障発見
サイクル数との平均値を寿命としたのは,あくまでも最ゆう推定法との比較のための便宜的な
処置である。
B.3.2 中途打切りデータの順位数
式(B.2)を用いて,平均順位jを計算する。
1
1
0
+
+
+
=
k
n
kj
j
········································································· (B.2)
ここに,
k: 逆順位,k=n+1−i,iは順位
j0: 直前の故障データに対する平均順位
n: 試験した全数,この例では12
計算結果を,表B.2に示す。ここで,直前の故障データに対する平均順位は,表のjの列ですぐ上の値
と同じであり,順位i=1の最初のデータについてはj0=0である。
B.3.3 メディアンランク
式(B.3)に対し平均順位jを用いて,メディアンランクpを計算する。
4.0
3.0
+
−
=nj
p
············································································ (B.3)
計算結果を,表B.2に示す。
注記1 式(B.3)は,JA.2.2に示す式(JA.4)のF(ti)をpに置き換えたものである。
表B.2に,この例の回帰計算を行うために使用したデータ及び計算結果を示す。
表B.2−中途打切りを含む連続測定の場合の寿命データ例(メディアンランク回帰法を適用)
標本番号
寿命サイクル数
状態
順位i
逆順位k
平均順位j
メディアンランクp
5
2.85×106
故障
1
12
1.00
0.056
12
5.5×106
故障
2
11
2.00
0.137
1
11.5×106
故障
3
10
3.00
0.217
4
15.0×106
中途打切り
4
9
−
−
9
17.0×106
故障
5
8
4.11
0.307
2
22.7×106
故障
6
7
5.22
0.396
8
31.6×106
故障
7
6
6.33
0.486
10
35.0×106
中途打切り
8
5
−
−
3
39.3×106
故障
9
4
7.66
0.593
11
42.4×106
故障
10
3
9.00
0.701
6
52.4×106
故障
11
2
10.33
0.808
7
55.9×106
打切り
12
1
−
−
注記2 回帰計算は,pをF(ti)と読み換えて,JA.3.2に示す方法で行う。
η
β
ln
1
+
=
Y
X
······································································· (B.4)
16
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
X: X=ln t
Y: Y=ln ln(1/1−p)で,pは式(B.3)による。
B.3.4 解析結果
図B.2に,解析結果を示す。計算に用いた故障寿命は表B.2の寿命サイクル数を使用しているが,デー
タの範囲は表B.1に示されている。
データに当てはめた直線及びそれに基づく母数の推定値は,メディアンランク回帰法によっており,信
頼限界はフィッシャーのマトリックス法に基づいている。
B.3.5 母数の推定値
− 尺度母数(特性寿命):η=41.0×106サイクル
− 形状母数(ワイブル係数):β=1.06
B.3.6 B10寿命の推定値
B.2.4と同様にして,式(B.1)でF(t)=0.1とおきB.3.5による母数の値を用いてB10寿命を計算すると,こ
の場合は次のようになる。
B10=4.91×106サイクル
B.3.7 B10寿命の信頼限界
95 %信頼水準におけるB10寿命の信頼限界は,フィッシャーのマトリックス法から,次の値となる。
2.1×106サイクル
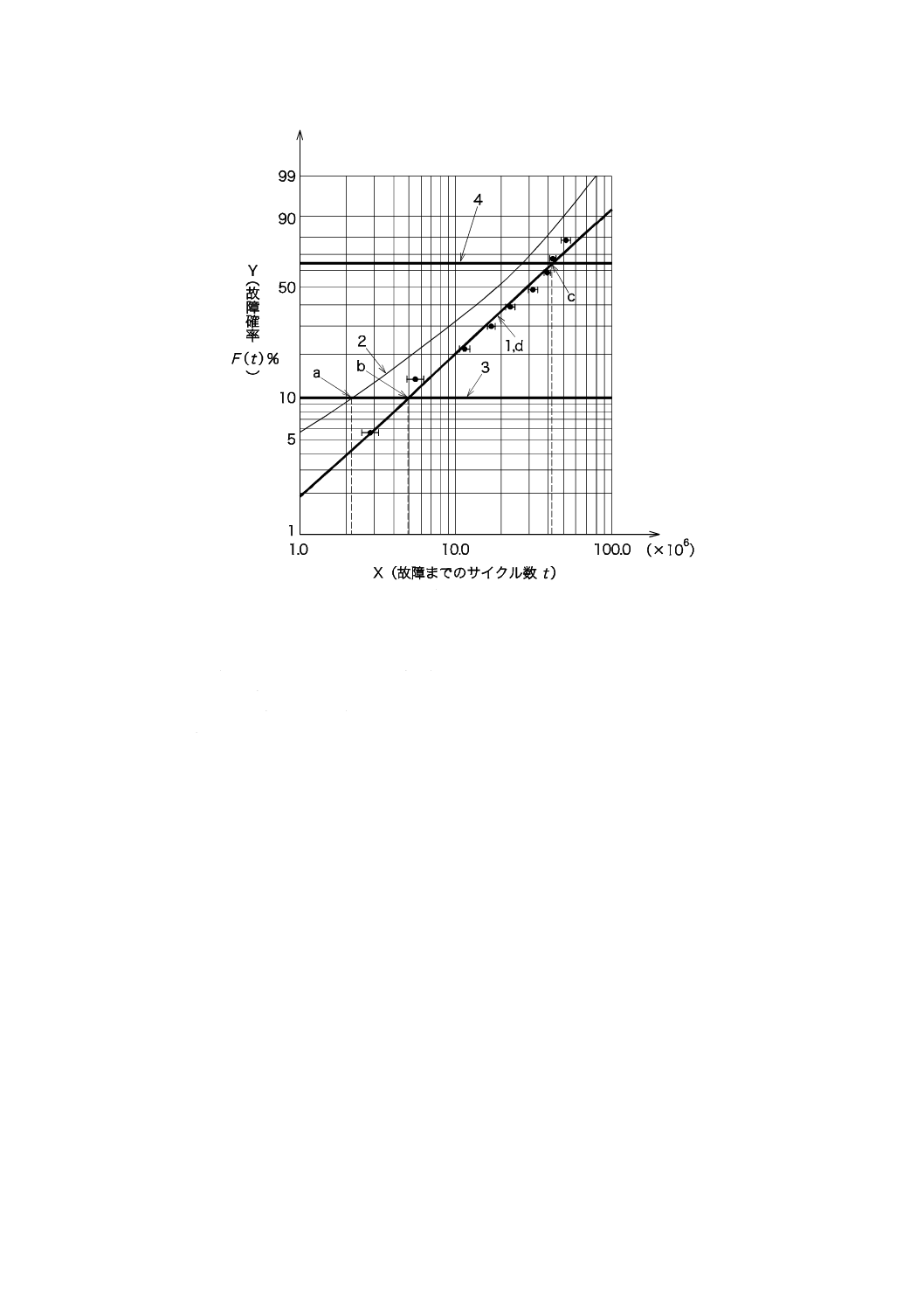
1
最ゆう推定法による直線
2
フィッシャーのマトリックス法による
95 %信頼限界
3
故障確率F(t)=10 %の線
4
故障確率F(t)=63.2 %の線
a
信頼水準95 %における
B10寿命の信頼限界
b
B10寿命
c
特性寿命η,この場合36.5×106サイクル
図B.1−中途打切りを含むデータの最ゆう推定法による解析結果(表B.1のデータ)
17
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
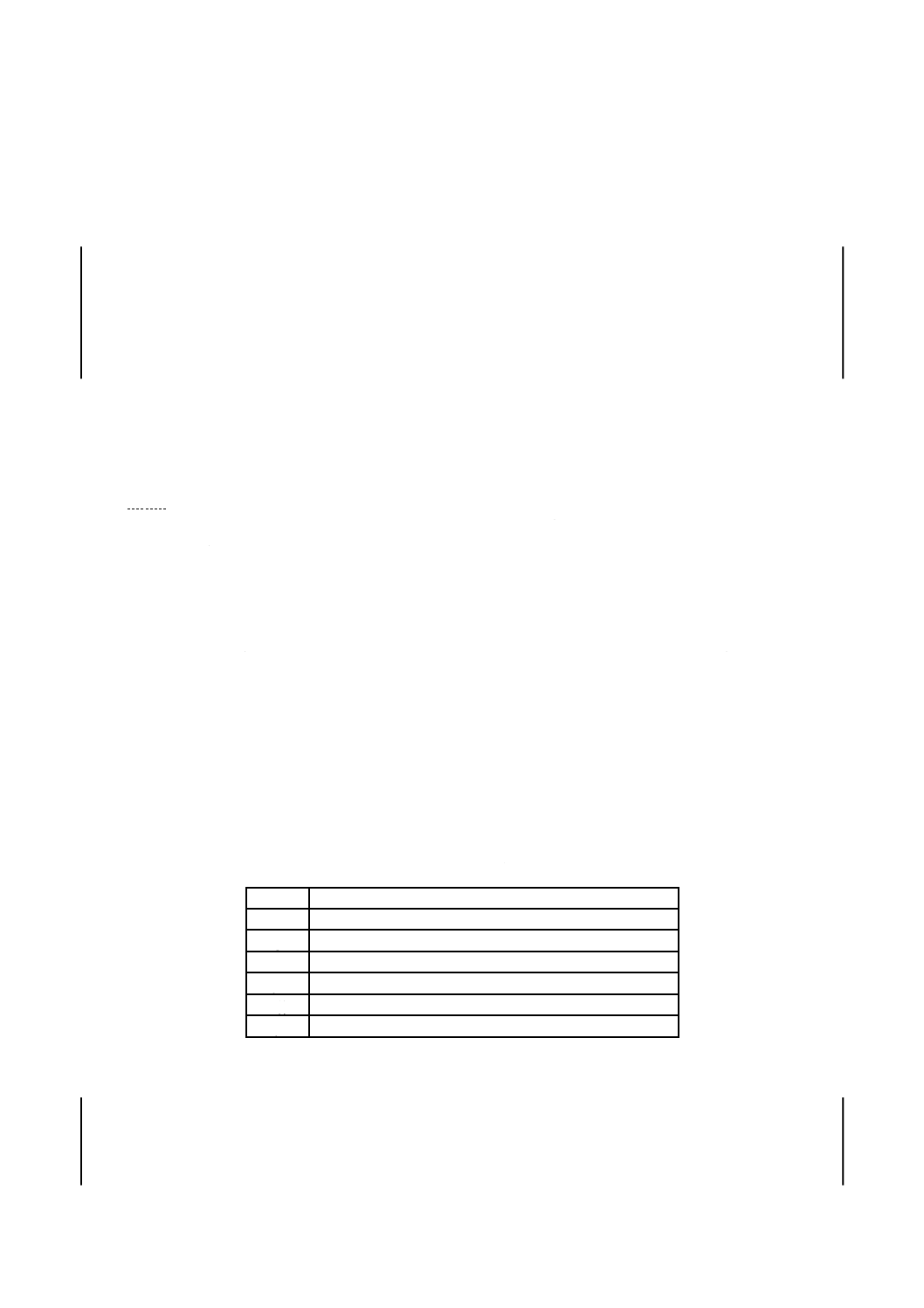
1
メディアンランク回帰法による直線
2
フィッシャーのマトリックス法による95 %信頼限界
3
故障確率F(t)=10 %の線
4
故障確率F(t)=63.2 %の線
a
信頼水準95 %におけるB10寿命の信頼限界
b
B10寿命
c
特性寿命η,この場合41.0×106サイクル
d
ワイブル係数βは1.06
図B.2−中途打切りを含むデータのメディアンランク回帰法による解析(表B.2のデータ)
18
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
指定の信頼度に対する寿命の実証試験
C.1 概要
この附属書では,指定の信頼度に対する製品の最小寿命がある基準値以上であることを,所定の信頼水
準で実証する方法について示す。この試験では母集団の故障寿命分布を推定するのではなく,ただ母集団
の寿命の片側信頼限界が,基準値より長寿命側にあることを試験によって証明するだけである。
この方法の利点は,試験全体に要する時間を箇条10に規定した方法より,短くできることにある。
C.2 前提条件
前提として,母集団の寿命分布はワイブル分布に従うものであり,その形状母数(ワイブル係数)は過
去の経験及び故障モードに関する技術的判断から,既知でなければならない。
注記 形状母数は,一般に故障モードと関連してある範囲の値をとると考えられている。過去の経験
からいろいろな値があり,どれをとるか決めかねる場合には,小さめの値を採用すれば安全側
の評価となる。
C.3 試験方法
試験は,通常の信頼性試験と同様な方法で,この規格の該当する部の規定に従って行う。この場合,製
品に要求される信頼度及びその信頼水準,試験個数などに応じて,与えられた基準値の寿命時間より長く
した割増し試験時間をあらかじめ設定しておき,その割増し試験時間内に標本が故障しなければ合格とす
る。全ての標本が合格であれば,その信頼度に対する母集団の最小寿命が基準値以上であることを,所定
の信頼水準において実証できたといえる。
C.4 記号
この附属書で用いる記号及び定義を,表C.1に示す。
表C.1−記号及び定義
記号
定義
t
試験による故障寿命(サイクル数又は距離)
tp
指定の信頼度に対する基準寿命
n
標本の大きさ
β
ワイブル分布の形状母数(ワイブル係数),既知とする。
R(t)
tにおける信頼度
γ
所定の信頼水準
C.5 問題の定式化
C.5.1 目的
指定の信頼度に対する母集団の基準寿命に対し,標本の最短寿命がそれを下回らないことを所要の信頼
水準において実証するため,試験時間を長くした割増し試験時間を求める。この場合,ワイブル係数は既

19
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
知とする。
C.5.2 基本式
寿命tにおけるワイブル分布の信頼度関数は,式(C.1)で表される。ワイブル係数βは既知である。
−
=
β
η
t
t
R
exp
)
(
································································· (C.1)
両辺の対数をとり,基準寿命tpに対する値との比をとり整理すると,式(C.2)のようになる。R(tp)は指定
された信頼度である。
β
1
)
(
ln
)
(
ln
=
p
p
t
R
t
R
t
t
····································································· (C.2)
tを割増し試験時間と考えると,割増し率は式(C.2)の右辺の値となる。
C.5.3 式の展開
製品n個を時間tまで試験して1個以上が故障する確率は,最大に見積もっても1−R(t)nであるが,こ
れが1に近いある確率γより更に大きいとする仮説1−R(t)n>γを設けたとき,試験では全く故障が起こら
なければ,その仮説は否定されたことになる。すなわち,1−γ≦R(t)nと考えなければならない。γは信頼
水準である。
不等号を等号に置き換えて整理すると,式(C.3)及び(C.4)が得られる。
n
t
R)
(
1
=
−γ
··········································································· (C.3)
)
1
ln(
1
)
(
ln
γ
−
=n
t
R
·································································· (C.4)
この関係を式(C.2)に代入して整理すると,次のようになる。
β
1
=
n
A
t
t
p
············································································ (C.5)
ただし,
)
(
ln
)
1
ln(
pt
R
A
γ
−
=
·········································································· (C.6)
係数Aは要求される信頼度と信頼水準とから決まる値で,これに標本の大きさn及びワイブル係数βを
加味して割増し試験時間が決まる。実証試験は,式(C.5)で決まる値以上の割増し時間について行わなけれ
ばならない。例えば,信頼水準γ=0.95で,指定の基準寿命がtp=B10とすると,指定信頼度はR(tp)=0.90
であるから,A=28.43となる。試験時間の割増し率は,これに標本の大きさn及び既知のワイブル係数β
を考慮して,式(C.5)によって決まることになる。
C.5.4 計算例
ある空気圧シリンダ10個を用い,母集団がB10=10 000 kmを満たしていることを信頼水準95 %で実証
するためには,どの位の割増し試験が必要かを求める。ただし同様な設計の他の製品から,ワイブル係数
はβ=2.0であることが分かっているとする。C.5.3からA=28.43として式(C.5)を用いると,次の式のよう
になる。
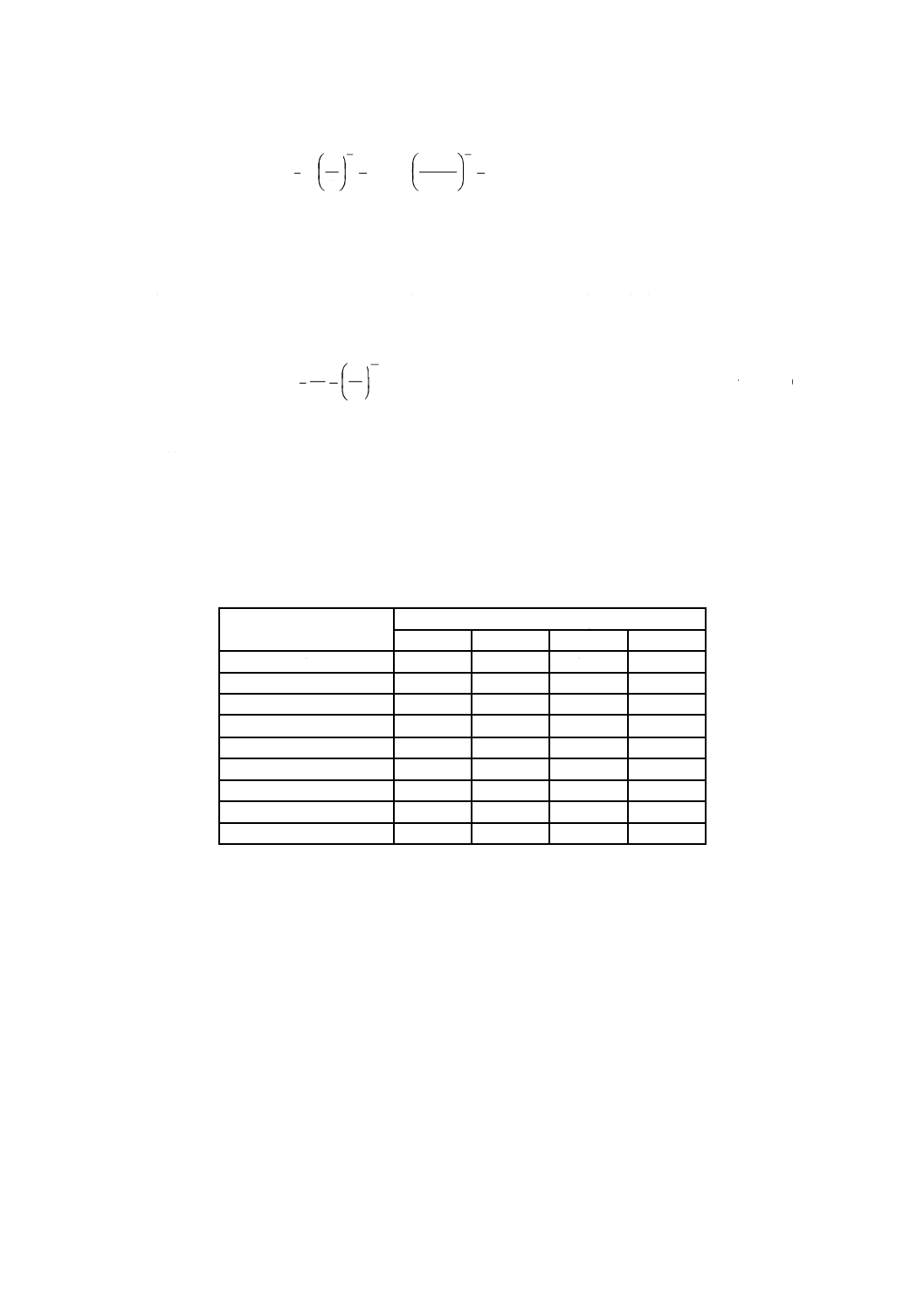
すなわち,この場合,シリンダ10個全てが16 860 km以上の試験に耐えたならば,母集団がB10=10 000
kmを満たしていることを信頼水準95 %で実証できたことになる。
20
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
860
16
10
43
.
28
000
10
2
1
2
1
=
=
=
n
A
t
t
p
C.6 B10寿命に対する試験時間の割増し率
C.6.1 計算式
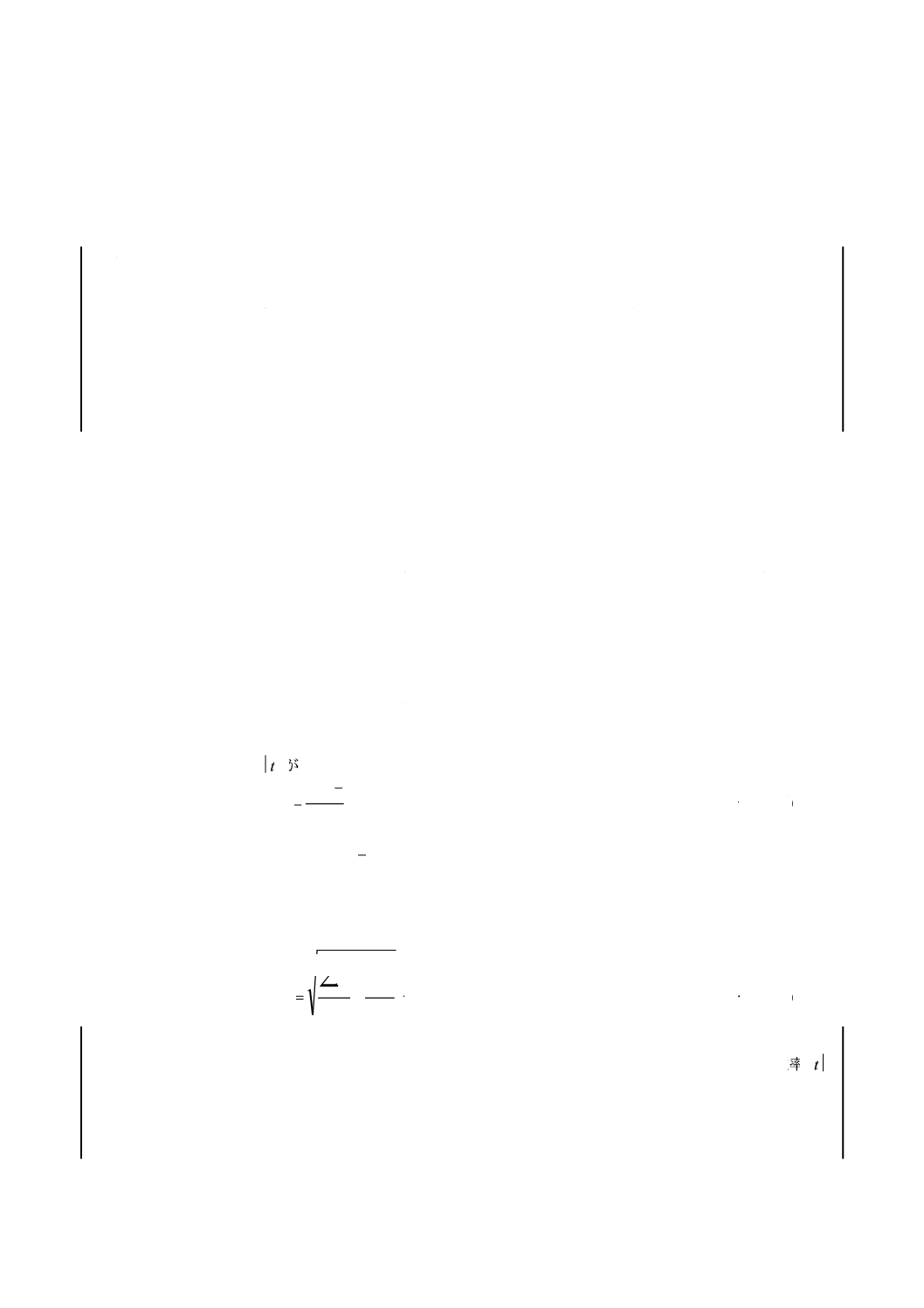
B10寿命を信頼水準95 %で実証することを考える。式(C.5)から試験時間の割増し率Lは次のように表さ
れる。
β
1
=
=
n
A
t
t
L
p
······································································· (C.7)
この場合,A=28.43なので,割増し率は表C.2のようになる。
C.6.2 計算例
ワイブル係数βを2.0とした場合,大きさ7の標本を用いて,B10=10 000 kmを信頼水準95 %で実証す
るには,どの位の試験時間が必要かを考える。
表C.2によればL=2.02であるから,割増し試験時間はt=20 200 kmとなる。
表C.2−信頼水準95 %におけるB10寿命実証のための試験時間の割増し率L
試験数n
ワイブル係数β
1.0
1.5
2.0
2.5
2
14.2
5.87
3.77
2.42
3
9.48
4.48
3.08
2.12
4
7.11
3.70
2.67
1.92
5
5.69
3.19
2.38
1.78
6
4.74
2.82
2.18
1.68
7
4.06
2.55
2.02
1.60
8
3.55
2.33
1.89
1.53
9
3.16
2.15
1.78
1.47
10
2.84
2.01
1.69
1.42
21
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
試験データにおける異常値の取扱い
D.1 概要
信頼性評価において,収集したデータの中のあるものが異常値ではないかと疑われる場合がある。この
附属書では,疑わしいデータを識別する方法及びそれを異常値として解析対象から除外すべきかどうかを
判断する方法を示す。
このような判断が必要な理由は,データ収集に的確さを欠いた可能性,試験中偶然に不具合が起こった
可能性,更にその他の異常があった可能性など,何らかの理由によってそのデータが母集団に属するもの
か,疑念がもたれることがあるからである。
D.2 原理
一連の測定データの中に,あらかじめ設定したある小さな確率値pthに対し,それを更に下回る確率でし
か起こらないと予測される極端なデータが含まれている場合,それは異常値として除外する。ここで推奨
する限界確率はpth=0.05であるが,これは他のデータより極端に大きいデータ及び極端に小さいデータの
両方を含む確率である。この基準に見合うデータは信頼度評価から除外することができるが,データは異
常値として報告しなければならない。
D.3 異常値の決定方法
D.3.1 疑わしいデータの識別
まず異常値かもしれない,疑わしい寿命データを識別する必要がある。このため,大きさnの標本によ
る試験では,得られた寿命の標本平均x及び標本標準偏差sを用いて,次の式から各データに対するt値
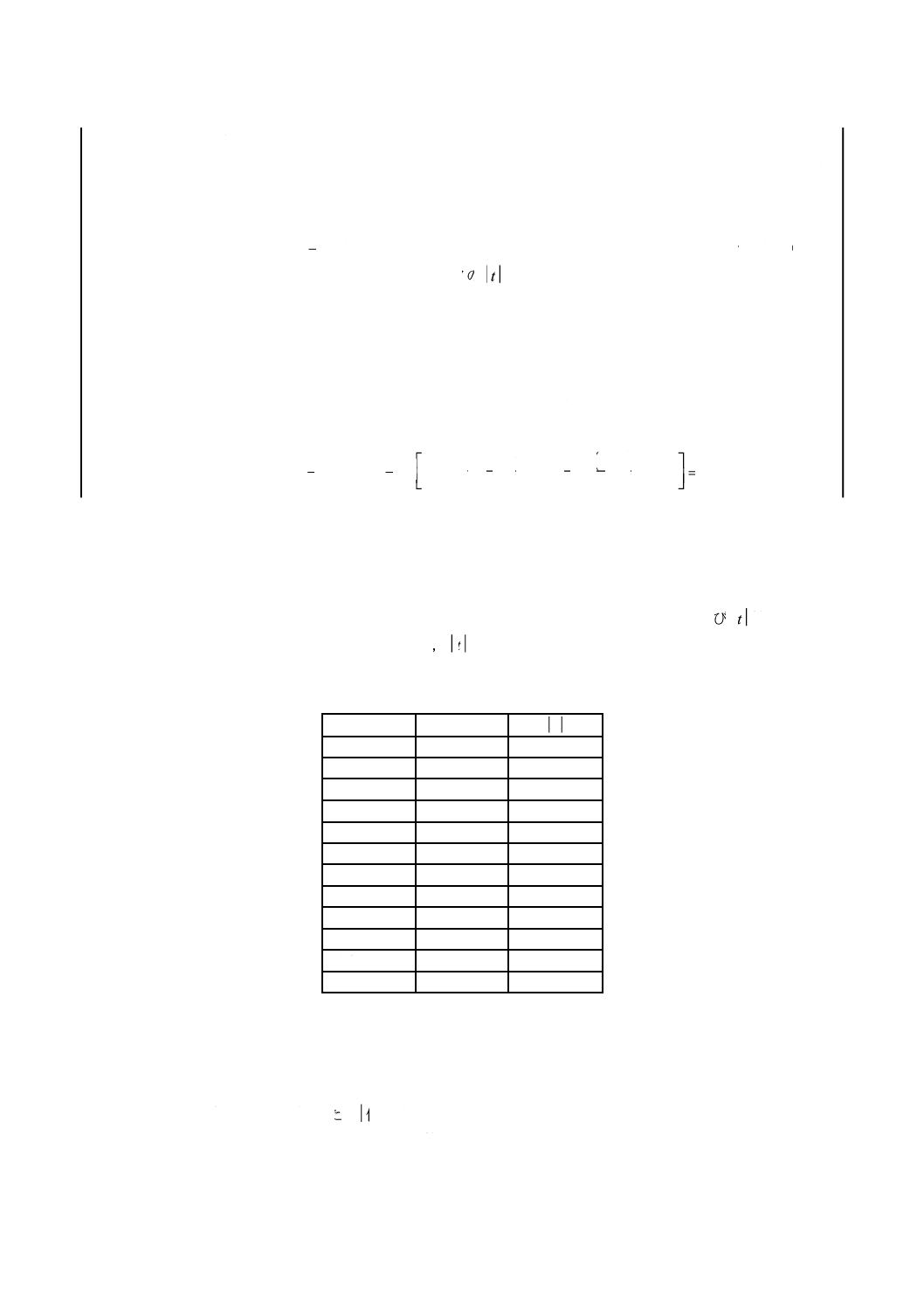
を計算する。tの絶対値
t
が異常に大きいデータは,疑わしいデータである。
s
x
x
t
i−
=
·············································································· (D.1)
ここに,
x: 個別の標本の寿命
x: 寿命の標本平均
s: 寿命の標本標準偏差
なお,標本標準偏差は,式(D.2)で求める。
注記 式(D.1)のt値は,t分布に従うことが知られている。
(
)
1
1
2
−
−
=∑
=
n
x
x
s
n
i
i
···································································· (D.2)
D.3.2 異常値の判定基準
疑わしいデータが異常値であると判定する基準は,母集団からそのような極端なデータを得る確率
t
値が,ある値より大きくなる確率pexを求め,それが限界確率pth以下のときとする。確率pexは,自由度(疑
わしいデータを含む。)n−1,並びに標本平均x及び標本標準偏差(疑わしいデータを除く。)sの関数で
ある。
22
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.3.3 疑わしいデータの生起確率
疑わしいデータの生起確率をpexとすると,大きさnの標本に疑わしいデータが全く含まれない確率は (1
−p)nであるから,標本に1個以上の疑わしいデータを含む確率は1−(1−p)nである。すなわち,pexは式(D.3)
のように表すことができる。
n
ex
p
p
)
1(
1
−
−
=
······································································ (D.3)
ここで,pは累積確率であるから,疑わしいデータの
t
の値を累積確率pに換算する必要がある。
注記 この計算は,t分布に関する市販のソフトウェア等を用いて行ってよいが,この場合pは両側確
率であることに注意する。
得られた疑わしいデータの生起確率pexが推奨の限界値pth=0.05より小さければ,これを異常値と判定
して信頼性評価対象から除外することができる。ただし,データは異常値として報告しなければならない。
なお,np<0.01の場合は,式(D.3)を級数に展開してpの高次項を無視することによって,式(D.4)のよう
に簡略化することができる。
(
)
(
)
(
)(
)
np
p
n
n
n
p
n
n
np
p
p
n
ex
≅
+
−
−
−
−
+
−
−
=
−
−
=
Λ
3
2
6
2
1
2
1
1
1
1
1
······· (D.4)
D.4 適用例
D.4.1 例1(異常値と判定されない例)
D.4.1.1 試験から得られたデータ
表D.1の10個の測定値は,実験室で得られた試験結果である。平均x,標準偏差s及び
t
値も示して
ある。疑わしいデータは番号10に関するもので,
t
=2.111と他より大きい。
表D.1−例1のデータ
番号
試験結果
t
1
53.785
0.393
2
52.367
0.668
3
55.684
0.026
4
57.251
0.278
5
50.203
1.087
6
61.085
1.021
7
49.226
1.277
8
55.577
0.046
9
56.267
0.088
10
66.712
2.111
平均x
55.816
−
標準偏差s
5.162
−
D.4.1.2 異常判定のための検討
次に,疑わしい値を除いて平均及び標準偏差を再計算する。その理由は,残りの9個の値を用いるほう
が,母平均及び母標準偏差のより良い推定値が得られると考えられるからである。
表D.2では,データは再計算した
t
値の降順に並べ直し,対応する累積確率pの値を示してある。この
確率は,適当な統計ソフトウェア等によって計算してよい。

23
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.2−異常判定のため再計算した例1のデータ(並べ直し)
順位
試験結果
再計算した t
累積確率p
1
66.712
3.297
0.009 3
2
49.226
1.465
0.177
3
50.203
1.199
0.261
4
61.085
1.765
0.111
5
52.367
0.610
0.557
6
53.785
0.223
0.828
7
57.251
0.721
0.489
8
56.267
0.453
0.661
9
55.577
0.265
0.797
10
55.684
0.294
0.776
新しい平均x
54.605
−
−
新しい標準偏差s
3.672
−
−
D.4.1.3 結果の判定
表D.2から,疑わしいのは順位1のデータで,平均値から3.3シグマ(標本標準偏差の3.3倍)ほど上に
外れているが,それは累積確率として0.93 %であることが分かる。大きさ10の標本の中にこのような極
端なデータを少なくとも一つ含む確率を式(D.3)から求めると,次のようになる。
pex=1−(1−0.009 3)10=0.089
すなわち,大きさ10の標本にこのような極端なデータが起こる確率はpex=8.9 %であり,これは判断基
準とするpth=5 %より大きいから,異常値ではないと判定される。したがって,これは信頼性評価に含め
なければならない。
注記 同じ計算を式(D.4)の簡略計算で行うと,pex ≅ np=0.089となる。
D.4.2 例2(異常値と判定される例)
D.4.2.1 対象とするデータ
表D.3に,大きさ10の標本による別のデータ例を示す。解析の手順は,D.4.1と同じである。
表D.3−例2の元のデータ(左)及び再計算したデータ(右)
元のデータ
再計算したデータ
番号
試験結果
t
順位
試験結果
再計算した t
累積確率p
1
56.241
0.253
1
79.057
6.424
0.000 122
2
57.177
0.137
2
48.658
2.035
0.072
3
56.120
0.269
3
59.800
1.065
0.315
4
57.361
0.114
4
51.841
1.150
0.280
5
48.658
1.196
5
59.688
1.034
0.328
6
59.688
0.175
6
57.361
0.387
0.708
7
56.864
0.176
7
57.177
0.335
0.745
8
59.800
0.189
8
56.864
0.248
0.809
9
51.841
0.800
9
56.241
0.075
0.942
10
79.057
2.582
10
56.120
0.041
0.968
平均x
58.280
−
新しい平均x
55.972
−
−
標準偏差s
8.048
−
新しい標準偏差s
3.593
−
−
24
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.4.2.2 解析結果
D.4.1.3と同様に,大きさ10の標本の中に累積確率が0.012 %であるような極端なデータを少なくとも一
つ含む確率は,この場合,式(D.4)を適用すると次のようになる。
pex=10×0.000 122=0.001 22
すなわち,大きさ10の標本にこのような極端なデータが起こる確率は,判断基準の5 %よりずっと小さ
い約0.1 %であり,それが起こったのであるから,これは異常値と判定される。したがって,順位1のデ
ータは信頼性評価から除外してよいが,データは異常値として報告しなければならない。
25
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
ワイブル解析のための数学的補遺
JA.1
概要
この附属書では,寿命試験データにワイブル分布を当てはめて母数及び信頼限界を推定する,いわゆる,
ワイブル解析のための数学的基礎について示す。箇条7の注4)では,ワイブル解析に際して市販のソフト
ウェアを使用してよいと記載しているが,この附属書は,正しいソフトウェアの選定,利用又は開発を助
ける目的で,メディアンランクによる故障確率の決定法,メディアンランク回帰法,最ゆう推定法による
母数の推定法,及びフィッシャーのマトリックスによる信頼限界の決定法について示す。
JA.2
メディアンランク
JA.2.1
信頼度及び故障確率
信頼度とは,ある製品の母集団が所定の寿命時間まで必要な機能を果たすことのできる確率の推定値で
ある。信頼度は寿命時間によって変化するので,R(t)のように寿命時間tの関数として表す。これに対し,
ある寿命時間までの母集団に関する故障確率の推定値は不信頼度と呼ぶことがあるが,これをF(t)とする
と,式(JA.1)の関係がある。
R(t)=1−F(t) ········································································· (JA.1)
ワイブル分布関数は故障確率について定義され,式(JA.2)のようであるから,信頼度を表す関数は式
(JA.3)のようになる。
()
−
−
=
β
η
t
t
F
exp
1
,t≧0 ··················································· (JA.2)
()
−
=
β
η
t
t
R
exp
································································ (JA.3)
したがって,故障確率,すなわち,不信頼度を求めれば,信頼度が分かる。
注記 故障確率は一般に記号pで表すことも多いが,全く同じ意味である。
JA.2.2
故障確率の推定方法
n個の製品からなる標本を試験した場合を考える。試験の結果,標本の全てが故障し,n個の寿命の観測
データが得られたとする。データを小さい方から大きい順に並べ直したものを順序統計量というが,この
場合は,t1≦t2≦……≦ti≦……≦tnとなる。このような順序統計データは,同一母集団から採った種々の標
本について求めると少しずつ異なっているが,全体としてはほぼ一定の性質をもつ。そこで,このような
標本についてのデータから,母集団の性質を推定する。
寿命時間tiに対する故障確率は,nが非常に大きいときは,ほぼF(ti)=i/nと推定できる。しかし,nが
小さいときは,異なる標本による順序統計量ごとのデータのばらつきが無視できなくなるため,推定した
故障確率の値もばらつく。
この問題を避けるため,故障確率のばらつきの中央値,すなわち,メディアンを理論的に求めて用いる。
これがメディアンランク法である。ただし,この計算は複雑なので,一般には次の近似式を用いる。
26
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
4.0
3.0
+
−
=ni
t
Fi
······································································· (JA.4)
ここに,
i: 順序統計量の中でのデータの順位
n: 標本の大きさ
なお,式(JA.4)による故障確率の推定は,中途打切りを含まない打切りデータ(附属書A参照),及び中
途打切りを含む打切りデータ(附属書B参照)にも,それぞれ注意点はあるが,適用できる。
JA.2.3
適用例
標本の大きさn=7,データの順位i=4の場合について考える。式(JA.4)を適用すると,寿命時間t4に対
する故障確率は式(JA.4' )になる。
()
5.0
4.7
7.3
4.0
7
3.0
4
4
=
=
+
−
=
t
F
······················································ (JA.4' )
このように,nが奇数の場合には,順序統計の中央に位置するデータに対しては,故障確率は常に0.5
である。また,n=7,i=1の場合に対する故障確率は,同様に計算するとF(t1)=0.095となり,故障確率
10 %の寿命B10は,t1より少し大きいことが分かる。これが9.2で標本の大きさを7個以上としている理由
である。
JA.3
メディアンランク回帰法
JA.3.1
一般事項
大きさnの標本について寿命試験を行い,r個の故障寿命データを得たとする。これを順序統計量とし
て故障時間とメディアンランクとの関係を求めるため,この規格では次の二つの方法を示している。
a) 中途打切りを含まないデータの場合 附属書Aによる。
b) 中途打切りを含むデータの場合 附属書Bによる。
この結果,寿命データtiに対応する故障確率としてF(ti)が得られたとする。r個のこのようなデータに対
しワイブル関数を当てはめて,最も確からしい分布の母数を求める手順を,次に示す。
JA.3.2
メディアンランク回帰法による母数の推定
まず,式(JA.2)を移項して両辺の自然対数を二回とると,次の式が得られる。
()
η
β
ln
1
1
ln
ln
1
ln
+
−
=
i
i
t
F
t
······················································· (JA.5)
この形は,更に次のように変数変換を行うと,簡単な一次式になる。
η
β
ln
1
+
=
i
i
y
x
······································································ (JA.6)
ただし,
i
i
t
x
ln
=
()
i
i
t
F
y
−
=
1
1
ln
ln
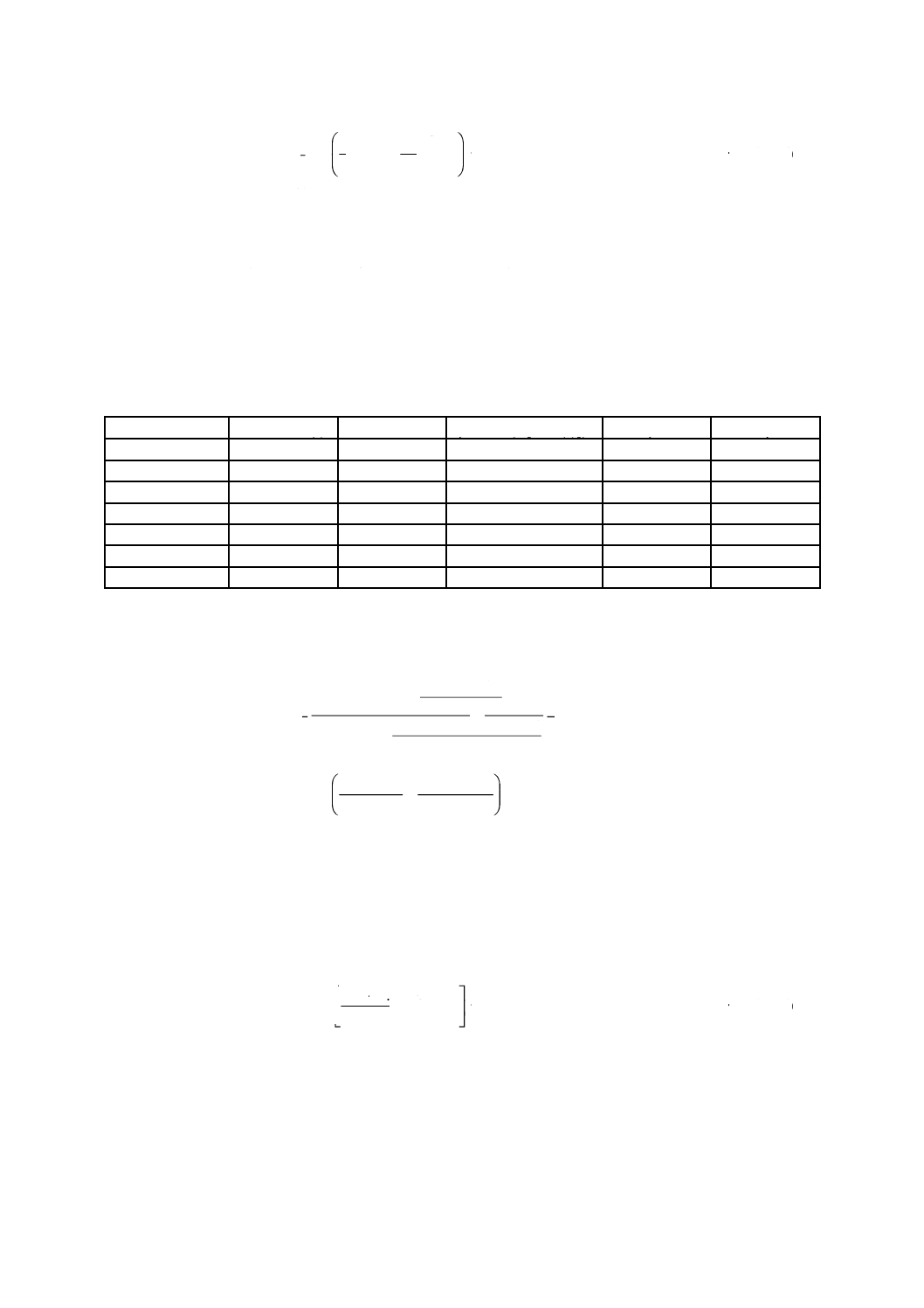
通常の最小二乗法を適用すると,形状母数β及び尺度母数ηは,次のように求めることができる。
∑
∑
∑
∑
∑
=
=
=
=
=
−
−
=
r
i
r
i
i
r
i
i
i
i
r
i
i
r
i
i
y
x
r
y
x
y
r
y
1
1
1
2
1
1
2
1
1
β
······················································· (JA.7)
27
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
=
∑
∑
=
=
r
i
i
r
i
i
y
r
x
r
1
1
1
1
exp
β
η
······················································ (JA.8)
注記 この場合,回帰計算においては,寿命(この場合はその対数)を表すxを目的変数としている。
yはメディアンランクの定義によって,式(JA.4)から確定値が与えられているのに対し,xは製
品ごとの寿命のばらつきを含む確率量だからである。
なお,寿命の対数を目的変数とすることは,寿命の対数の等分散性を仮定することになるが,
それは寿命の等変動係数性を考えていることと等しいから,その意味でも合理的といえる。
JA.3.3
適用例
例として,次の完全データが得られた場合の母数を推定する。表JA.1に計算の過程を示す。
表JA.1−メディアンランク回帰法による計算
終了サイクル数ti
不信頼度F(ti)
xi=ln ti
yi=ln ln{1/[1−F(ti)]}
yi2
xi yi
16×106
0.11
2.772 59
−2.155 62
4.646 68
−5.976 64
34×106
0.27
3.526 36
−1.175 27
1.381 26
−4.144 43
53×106
0.42
3.970 29
−0.601 54
0.361 85
−2.388 30
75×106
0.58
4.317 49
−0.147 29
0.021 69
−0.635 91
93×106
0.73
4.532 60
0.281 92
0.079 48
1.277 82
120×106
0.89
4.787 49
0.794 34
0.630 97
3.802 88
計
−
23.906 82
−3.003 46
7.121 94
−8.064 58
式(JA.7)及び式(JA.8)と表JA.1の計算結果から,メディアンランク回帰法におけるβ及びηは,次のよ
うに求まる。
66
439
.1
6
)
46
003
.3
(
82
906
.
23
58
064
.8
6
)
46
003
.3
(
49
121
.7
2
=
−
×
−
−
−
−
=
β
6
109
.
76
6
66
439
.1
46
003
.3
6
82
906
.
23
exp
=
×
−
−
=
η
JA.4
最ゆう推定法
JA.4.1
一般
ゆう(尤)度とは,想定した母集団の分布関数に観測値を当てはめた結果の確率のことであり,観測値
が想定した分布関数にどの程度よく適合しているかを表す尺度の一つである。寿命データの場合は,ある
寿命時刻までに故障しているか否かの二項分布として,式(JA.9)のゆう度Lを考えるのが一般的である。
(
)
(
)
∏
+
=
−
+
=
r
m
i
r
m
R
R
r
m
r
m
L
1
1
!
!
!
······················································ (JA.9)
ここに,
i: n個中の小さい方から数えたデータ順位
m: 時点tiにおいて正常に稼働している製品の数
r: 時点tiまでに故障した製品の数
R: 分布関数から予測される時点tiにおける信頼度
なお,式(JA.9)の記号Πは,m+r組のデータに対する各値の積を表す。また,時点tiにおいて正常稼働
数m及び故障数rを記録していたとして,ti+1において新たに故障1件を確認したとすると,ti+1にお
28
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ける正常稼働数はm−1,故障数はr+1となる。すなわち,m及びrは,tiとともに順次変わる値である。
注記 式(JA.9)のゆう度とは,母数β及びηが与えられたとき,その分布が観測したデータに照らして,
どの程度もっともらしい(尤もらしい)かの度合いを表している。
JA.4.2
最ゆう推定法による母数の推定
最ゆう推定法は,観測したデータに対し,ゆう度が最大になるように母数β及びηを定める方法である。
具体的には,式(JA.9)の両辺の自然対数をとると,式(JA.10)のようになるが,未知母数β及びηは式(JA.3)
を参照すれば明らかなように,Rに含まれているだけである。
そこで,式(JA.10)をβ及びηで偏微分して0とおき連立に解けば,ゆう度を最大にする母数β及びηを
求めることができる。結果を整理すると,式(JA.11)及び式(JA.12)のようになる。ただし,式(JA.11)は解析
的に解けないので,例えば,ニュートン・ラプソン法などの数値解法によって解く必要がある。得られた
βの値を式(JA.12)に入れれば,ηが求まる。
(
)
(
)
∑
+
=
−
+
+
+
=
r
m
i
R
r
R
m
r
m
r
m
L
1
1
ln
ln
!
!
!
ln
ln
··································· (JA.10)
∑
∑
∑
+
=
+
=
+
=
=
+
−
−
r
m
i
i
r
m
i
i
r
m
i
i
t
r
m
t
t
t
1
1
1
0
1
1
ln
β
β
β
················································ (JA.11)
β
β
η
1
1
1
+
=
∑
+
=
r
m
i
it
r
m
······························································· (JA.12)
JA.4.3
適用例
JA.3.2のデータを用いて,最ゆう推定法によって母数を推定する。ただし,JA.4.2にあるように,式(JA.11)
のβは一般的な数式で求めることは困難なため,ニュートン・ラプソン法による反復計算によって求めて
いる。具体的には,式(JA.11)の左辺をf(β)とおくと,あらかじめ決めておいた誤差εに対し,
ε
β
β
<
−
+
i
i
ˆ
ˆ1
に
なるまで
)
ˆ(
)
ˆ
(
ˆ
ˆ1
i
i
i
i
f
f
β
β
β
β
′
−
=
+
を反復計算し,
1
ˆ+
iβを解とみなす方法である。ここで,iは反復計算の回数
である。
計算過程を示すことはできないため,次に結果だけを示す。
β=1.932 678 η=73.525 48
注記 JA.3.2に示したメディアンランク回帰法による結果と,ここに示した最ゆう推定法による結果
とは通常一致しない。特に,βの推定量に違いが表れ,図JA.1に示すように最ゆう推定法によ
る値のほうが大きくなる。その一つの理由は,式(JA.9)などから分かるように,最ゆう推定法で
はRが0.5に近い場合にデータの重みが最も強調される傾向があるのに対し,メディアンラン
ク回帰法では寿命によらず等重みとして解析しているからである。したがって,B10などの信頼
度の低い領域のデータを重視したいときは,メディアンランク回帰法を用いるほうがよい。
JA.5
フィッシャーのマトリックスによる信頼限界
JA.5.1
一般事項
データに当てはめたワイブル関数の信頼限界を求める方法を,次に示す。
一般に信頼限界を求める方法には種々のものがあり,用いる方法によって得られる信頼限界は異なる。
この規格では11.4において,フィッシャーが提案したマトリックス法によって信頼限界を求めることを
29
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
規定している。この方法は,他法に比べて信頼区間の幅が狭くなる傾向があるといわれており,支持者が
多いとされる。
ここでは,片側信頼水準95 %におけるB10寿命の下側信頼限界を求める方法について示す。
注記 フィッシャーのマトリックス法では,所定の信頼度に対して推定した寿命時間の信頼限界を求
める場合,及び所定の時間に対して推定した信頼度の信頼限界を求める場合がある。このこと
は,ソフトウェアなどを用いるときに留意しなければならない。
JA.5.2
フィッシャーのマトリックス
式(JA.6)において,与えられた信頼度に対応する対数寿命x=ln tを推定する式を示した。既に母数が推
定されているときの期待値をxˆとすると,xˆの100(1−α) %下側信頼限界は,次によって求めることができ
る。
)ˆ(
ˆ
x
Var
K
x
xL
α
−
=
······························································ (JA.13)
ここに,
Kα: 標準正規分布の下側α %点,値は統計数値表などから読む。
xˆ: xの期待値
Var(xˆ): xˆの分散
ここで,xˆの分散は,式(JA.6)の関係から次の式で評価できるとされている。
()
()
()
()
η
η
η
β
η
β
β
β
ˆ
ˆ
1
ˆ
,ˆ
ˆ
ˆ
2
ˆ
ˆ
ˆ
2
2
4
2
Var
Cov
y
Var
y
x
Var
+
−
=
····························· (JA.14)
ここに,
Var(βˆ): βˆの分散
Var(ηˆ): ηˆの分散
Cov(βˆ,ηˆ): βˆとηˆの共分散
y:
()t
F
−
1
1
ln
ln
注記 式(JA.14)は,時間の信頼限界を求める場合の式である。
式(JA.14)を求めるためには,β及びηの分散及び共分散が知られていなければならない。これを求める
のが,フィッシャーのマトリックス法である。具体的には,式(JA.10)の対数ゆう度ln Lをβ及びηで2回
偏微分し,次のように計算を行う。
()
()
()
()
1
2
2
2
2
2
2
ln
ln
ln
ln
ˆ
ˆ
,ˆ
ˆ
,ˆ
−
∂
∂
−
∂
∂∂
−
∂
∂∂
−
∂
∂
−
=
η
η
β
η
β
β
η
η
β
η
β
β
L
L
L
L
Var
Cov
Cov
Var)
···························· (JA.15)
フィッシャーのマトリックスを書き下すと,行列の各要素は次のように表される。すなわち,大きさn
個の標本において,r個の故障データ(t1,t2,… tr),及び(n−r)個の打切りデータ(tr+1,… tn)が得られてい
る場合,式(JA.16)〜式(JA.18)になる。
∑
=
=
+
−
=
∂
∂
−
n
i
i
i
I
t
t
r
L
1
11
2
2
2
2
ln
ln
η
η
β
β
β
····································· (JA.16)
(
)
∑
=
=
+
+
−
=
∂
∂
−
n
i
i
I
t
r
L
1
22
2
2
2
2
1
ln
β
η
η
β
β
η
β
η
··································· (JA.17)
∑
=
=
=
+
−
=
∂
∂∂
−
n
i
i
i
I
I
t
t
r
L
1
21
12
2
ln
1
ln
η
ηβ
η
η
η
η
β
β
························· (JA.18)
したがって,逆行列の一般公式を用いると,式(JA.19)〜式(JA.21)になる。
30
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
22
Δ
1I
Var
=
β)
····································································· (JA.19)
()
11
Δ
1I
Var
=
η)
······································································ (JA.20)
(
)
12
Δ
1
,
I
Cov
=
η
β)
)
·································································· (JA.21)
ここに,
21
12
22
11
1
1
I
I
I
I
−
=
∆
このようにして得られた各値を,式(JA.14)に代入することでxˆの分散を求め,式(JA.13)からxˆの信頼下
限xLを導くことができる。推定寿命時間の100(1−α) %下側信頼限界は,式(JA.22)になる。
()
L
L
x
t
exp
=
········································································ (JA.22)
JA.5.3
適用例
例として,次の完全データが得られた場合の,時間の信頼限界における,B10の95 %下側信頼限界を推
定する。母数としては,β=1.932 7,η=73.525 5が得られているものとする。表JA.2及び式(JA.23)から式
(JA.25)に,各要素の計算結果を示す。
表JA.2−フィッシャーのマトリックス要素計算結果
終了サイクル数ti
(ti/η)β[ln(ti/η)]2
[β(β+1)/η2](ti/η)β
(ti/η)β[1/η+β/η ln(ti/η)]
16×106
0.122 040
0.000 055
−0.001 390
34×106
0.133 980
0.000 236
−0.001 503
53×106
0.056 917
0.000 557
0.002 654
75×106
0.000 410
0.001 089
0.014 675
93×106
0.086 943
0.001 651
0.031 145
120×106
0.618 460
0.002 702
0.068 240
計
1.018 750
0.006 291
0.113 821
03
625
.2
75
018
.1
7
932
.1
6
75
018
.1
2
2
11
=
+
=
+
=βr
I
························ (JA.23)
146
004
.0
291
006
.0
5
525
.
73
7
932
.1
6
291
006
.0
2
2
22
=
+
×
−
=
+
−
=ηβ
r
I
············ (JA.24)
217
032
.0
821
113
.0
5
525
.
73
6
821
113
.0
21
12
−
=
−
=
−
=
=
η
r
I
I
······· (JA.25)
したがって,フィッシャーのマトリックスは,次の式(JA.26)のように表せる。
()
()
()
()
1
146
004
.0
217
032
.0
217
032
.0
03
625
.2
ˆ
ˆ,ˆ
ˆ,ˆ
ˆ
−
−
−
=
η
η
β
η
β
β
Var
Cov
Cov
Var
····················· (JA.26)
分散・共分散行列は,最終的に式(JA.31)のように求められる。
277
570
.
101
4
845
009
.0
1
)
217
032
.0
217
032
.0(
146
004
.0
03
625
.2
1
1
=
=
×
−
×
=
∆
························· (JA.27)
31
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11
421
.0
146
004
.0
277
570
.
101
1
)ˆ
(
22
=
×
=
∆
=
I
Varβ
························ (JA.28)
024
625
.
266
03
625
.2
277
570
.
101
1
)ˆ(
11
=
×
=
∆
=
I
Varη
····················· (JA.29)
29
272
.3
217
032
.0
277
570
.
101
1
)ˆ
,ˆ
(
12
=
−
×
=
∆
=
I
Cov
η
β
·················· (JA.30)
=
024
625
.
266
29
272
.3
29
272
.3
11
421
.0
)ˆ(
)ˆ,ˆ(
)ˆ,ˆ(
)ˆ(
η
η
β
η
β
β
Var
Cov
Cov
Var
························· (JA.31)
これを用いて,式(JA.14)からB10寿命に対するxˆの分散を計算すると,次の値が得られる。
(
)
[
]
024
625
.
266
5
525
.
73
1
1
421
.0
9.0
ln
ln
7
932
.1
1
)ˆ(
2
2
4
×
+
×
−
=
x
Var
(
)
784
255
.0
29
272
.3
5
525
.
73
9.0
ln
ln
7
932
.1
1
2
2
=
×
−
−
+
··············· (JA.32)
一方,式(JA.6)からB10寿命に対するxˆの推定値を計算すると,ここではメディアンランク回帰法による
母数β=1.44及びη=76.11を用いた場合,次のようになる。
(
)
(
)
245
769
.2
11
.
76
ln
9.0
ln
ln
44
.1
1
ˆ
=
+
−
×
=
x
································ (JA.33)
28
937
.1
751
505
.0
645
.1
245
769
.2
)ˆ(
ˆ
=
×
−
=
−
=
x
Var
K
x
xL
α
··········· (JA.34)
94
.6
28
937
.1
=
=
=
e
e
t
L
x
L
·························································· (JA.35)
以上によって,B10寿命の95 %片側信頼限界として,6.94×106が得られた。
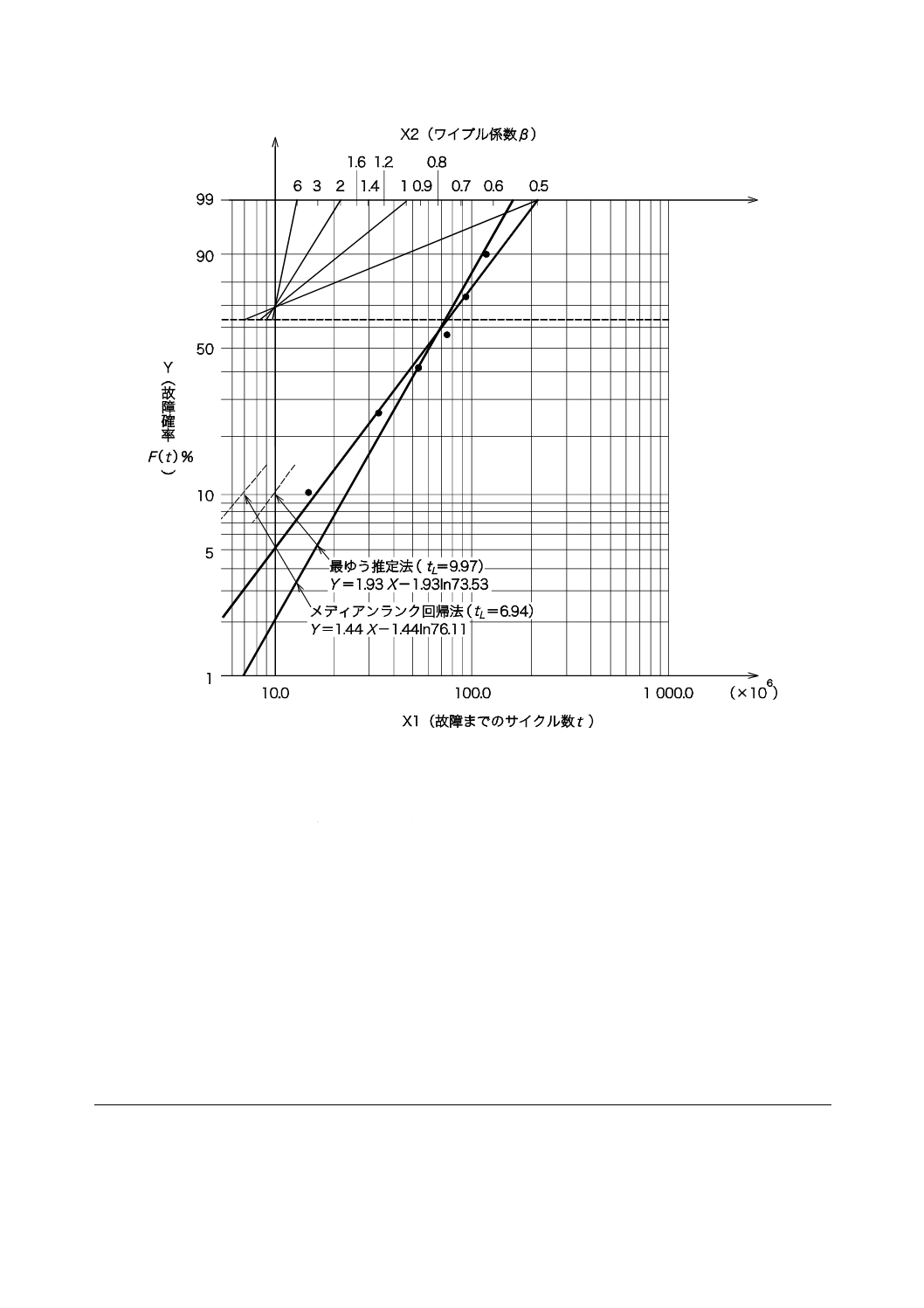
なお,この結果を最ゆう推定法による結果と合わせて図示すると,図JA.1のようになる。
32
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図JA.1−フィッシャーのマトリックス法によるB10寿命の信頼限界
注記 この規格,附属書A,附属書Bなどにおける連続した信頼限界線は,故障確率を連続的に変化
させて,このような解析を行って得られたtLをプロットしたものである。
参考文献 Abernethy, Robert; The new Weibull handbook, 5th ed., North Palm Beach, R.B.Abernethy, 2006.
http://www.weibull.com/;eText boos on Reliability, Life Data(Weibull) Analysis Reference, (Rev, 2005)
33
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
JISと対応国際規格との対比表
JIS B 8672-1:2011 空気圧−試験による機器の信頼性評価−第1部:通則
ISO 19973-1:2007 Pneumatic fluid power−Assessment of component reliability by
testing−Part 1: General procedures
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差異の
理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
1 適用範囲
1
適用範囲
変更,
追加
Noteの記載内容を,適用範囲に
入れ,新たに注記を追加。
規定内容をより明確にし,注記によっ
て追加説明を行っている。
ISO規格見直し時に修正を提案する。
4 記号及び
単位
4
記号及び単位
追加
表1に記号tを追加。
信頼性評価における関数(t)は,必ずし
も時間ではなく,定義を明確にした。
ISO規格見直し時に修正を提案する。
8 試験条件 8.3 試験環境
8.3
試験環境
変更
表2の空気の品質における露点
を+3 ℃から−20〜+7 ℃に
変更。
従来規格(JIS B 8392-1)との整合の
ため。
ISO規格見直し時に修正を提案する。
10 試験の
終了
10.1 要求最小故障数
10
試験の終了
変更
表3の要求最小故障数の
“>10”の記載を“11以上”に
変更。
理解を助けるため。
ISO規格見直し時に修正を提案する。
12 試験報
告書
12
試験報告書
追加
“母数を推定するためのグラ
フ”を報告書記載項目として追
加。
母数及び信頼性特性値を決定した証
拠を明確にするため。
ISO規格見直し時に修正を提案する。
附属書A
(参考)
A.1 概要
附属書A
(参考)
A.1 概要
追加
概要を追加し,附属書の位置づ
けを明確にした。
理解を助けるため。
ISO規格見直し時に修正を提案する。
A.2.4 B10寿命の推定値
A.2.4 式(A.1)
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
附属書B
(参考)
B.1 概要
附属書B
(参考)
B.1 概要
追加
概要を追加し,附属書の位置づ
けを明確にした。
理解を助けるため。
ISO規格見直し時に修正を提案する。
4
B
8
6
7
2
-1
:
2
0
11
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
34
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差異の
理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
附属書B
(参考)
(続き)
B.2.4 B10寿命の推定値
附属書B
(参考)
(続き)
B.2.4 式(B.1)
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
B.3.2 中途打切りデー
タの順位数
B.3.2 式(B.2)
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
B.3.3 メディアンラン
ク
B.3.3 式(B.4)
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
附属書C
(参考)
C.1 概要
附属書C
(参考)
C.1 概要
追加
概要を追加し,附属書の位置づ
けを明確にした。
理解を助けるため。
ISO規格見直し時に修正を提案する。
C.4 記号
C.4 記号
変更
削除
理論式の簡潔化に伴い,一部の
記号を変更又は削除した。
理解を助けるため。
ISO規格見直し時に修正を提案する。
C.5.1 目的
C.5.1 問題の定義及び
式の展開
変更
削除
理論式の簡潔化に伴い,題名及
び内容を変更した。
理解を助けるため。
ISO規格見直し時に修正を提案する。
C.5.2 基本式
C.5.1.2〜C.5.1.7の理論
式の展開
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
C.5.3 式の展開
C.5.1.8のFigure C.1
削除
係数Aがグラフ(図C.1)から
直接読み取れるわけではなく,
傾向を示すものだけであり,削
除した。
ISO規格見直し時に修正を提案する。
附属書D
(参考)
D.1 概要
附属書D
(参考)
D.1 概要
追加
概要を追加し,附属書の位置づ
けを明確にした。
理解を助けるため。
ISO規格見直し時に修正を提案する。
D.3 異常値の決定方法
D.3.3〜D.3.6の理論式
の展開
変更
削除
式の展開を簡潔な表現とした。
技術的差異はない。
理解を助けるため。
ISO規格見直し時に修正を提案する。
附属書JA
(参考)
−
−
追加
数学的補遺
理解を助けるため。
ISO規格見直し時に追加を提案する。
JISと国際規格との対応の程度の全体評価:ISO 19973-1:2007,MOD
4
B
8
6
7
2
-1
:
2
0
11
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

35
B 8672-1:2011
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
4
B
8
6
7
2
-1
:
2
0
11
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。