2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 3700-42:1996
(ISO 10303-42:1994)
産業オートメーションシステム
及びその統合
−製品データの表現及び交換−
第42部:統合総称リソース:
幾何及び位相の表現
Industrial automation systems and integration
−Product data representation and exchange−
Part 42 : Integrated generic resources :
Geometric and topological representation
序文 この規格は,1994年に第1版として発行されたISO 10303-42 (Industrial automation systems and
integration−Product data representation and exchange−Part 42 : Integrated generic resources : Geometric and
topological representation) を翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規
格である。
なお,この規格で側線を施してある“参考”は,原国際規格にはない事項である。
0. 序文 この規格群は,計算機で解読可能な製品データの表現及び交換のための国際規格とする。この
規格群は,製品のライフサイクルを通して,製品データを記述できる中立的な仕組みを特定の処理系に依
存しない方法で提供することを目的とする。こうした記述は,その性質上,中立的なファイル交換だけで
なく,製品データベースを作成・共有したり製品データを保管したりする際の基本としても適している。
この規格群は,一連の規格からなり,それらは別々に発行される。この規格群のそれぞれの規格は,記
述法,統合リソース,アプリケーションプロトコル,抽象試験スイート,実装法及び適合性試験に分けら
れる。これらの概要は,JIS B 3700-1に示されている。この規格は,統合リソースクラスの一つとする。
この規格の主な内容は,次のとおりとする。
− 幾何 (Geometry)
− 位相 (Topology)
− 形状モデル (Geometric models)
規格群の中で,この規格は,幾何及び位相表現に用いる統合リソースについて規定する。その主な応用
としては,製品モデルの形状又は幾何形式を明示的に表現することである。この形状表現は,物理ファイ
ルに展開されたときに,安定かつ効果的に情報伝達を行うために規定された。
幾何(4.)は,主にパラメタ曲線及びパラメタ曲面の幾何について規定する。ここには,それらの定義に必
2
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
要な曲線及び曲面のエンティティ,他のエンティティ,関数,並びにデータ型が含まれる。共通の枠組か
2次元と3次元との両方の幾何の定義に使われる。すべての幾何は,それらが表現する要素のコンテキス
トの一部として定められた一つの座標系の中で定義される。これらの概念は,すべてJIS B 3700-43に定義
される。
位相(5.)は,オブジェクトの幾何形状に関してではなく,オブジェクト間の接続関係について規定する。
ここには,基本的な位相エンティティとそれらが特殊化された下位型とか含まれる。ある場合には,その
下位型は,幾何的な関連付けをもつ。更に,位相エンティティの定義に必要な関数(特に制約関数)及び
データ型も含まれる。
形状モデル(6.)は,3次元立体オブジェクトの形状を記述するデータを交換するための基本的なリソース
を規定する。形状モデルは,(多くの場合)幾何と位相との両方のデータを含む,形状の完全な表現方法を
規定する。ここには,二つの古典的な形式の立体モデルであるCSG (Constructive Solid Geometry) と境界表
現 (B-rep) とが含まれる。更に,製品の幾何を記述するのにやや完全さに欠け,より整合性に関する制約
の少ない別のエンティティも,ここに含まれる。
1. 適用範囲 この規格は,製品形状の幾何及び位相の明示的な表現のためのリソース構造を規定する。
この規格の範囲は,理想的な製品モデルを明示的に表現する際に必要なものとする。公差及び形状特徴に
よる暗黙的な表現形式は,この規格では定めない。幾何(4.参照)及び位相(5.参照)は,独立に利用でき,
この規格でも形状モデル(6.参照)の種々の形式で広く使われる。更に,この規格では,表現要素が形状
に関する場合の表現概念を規定する。
1.1
幾何 (Geometry) 次のものは,幾何スキーマの範囲とする。
− 点,ベクトル,パラメタ曲線及びパラメタ曲面の定義。
− 変換に関する演算の定義。
− 直接座標値で,又は存在する曲線若しくは曲面のパラメタで定義された点。
− 円錐曲線及び初等曲面の定義。
− パラメタ曲面上の曲線の定義。
− 一般的なパラメタスプライン曲線及びパラメタスプライン曲面の定義。
− 点,曲線及び曲面の複製の定義。
− オフセット曲線及びオフセット曲面の定義。
− 交差曲線の定義。
次のものは,この規格の範囲外とする。
− 手続き的に定義した曲線及び曲面の他のすべての形式。
− パラメタ的な表現形式をもたない曲線及び曲面。
− 線織面の明示的な表現のすべての形式。
備考 線織面について,幾何は,境界曲線のパラメタ化及び二つの曲線上の点の組とを関連付け
る方法に大きく依存する。しかし,B-スプラインの境界曲線をもつ線織面は,B-スプライ
ン曲面エンティティで正確に表現できる。
1.2
位相 (Topology) 次のものは,位相スキーマの範囲とする。
− 基本的な位相エンティティである頂点,稜線及び面の定義。これらのエンティティは,特別な下
位型によって,それぞれ点,曲線及び曲面の幾何と関連付け可能とする。
− 位相構造である稜線列 (path),ループ及びシェルを形成する基本的な位相エンティティを集めた
3
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
もの,並びにこれらの構造の整合性を保証する制約。
− 位相エンティティの向き。
1.3
形状モデル (Geometric Shape Model) 次のものは,形状モデルスキーマの範囲とする。
− 3次元立体の正確な幾何形式を記述するデータ。
− CSG (constructive solid geometry) モデル。
− CSG基本立体及び半空間の定義。
− 掃引操作による立体モデルの生成。
− 多様体境界表現 (B-rep) モデル。
− 境界表現モデルの整合性を保証する制約。
− 曲面モデル。
− ワイヤフレームモデル。
− 幾何データ集合。
− 別な配置での立体モデルの複製の生成。
次のものは,この規格の範囲外とする。
− 非多様体境界表現モデル。
− 空間占有法による立体モデル(例えば,8進木モデル。)。
− 組立て品及び機構。
2. 引用規格 この規格は,次の規格を引用する。
(1) ISO/IEC 8824-1 : 1) Information technology−Open Systems Interconnection−Abstract Syntax
Notation One (A S N.1) −Part 1 : Specification of basic notation
注1)
近く,発行予定。
(2) ISO 10303-1 : 1994 Industrial automation systems and integration−Product data representation and
exchange−Part 1 : Overview and fundamental principles
備考 JIS B 3700-1(産業オートメーションシステム及びその統合製品−データの表現及び交換−
第1部:概要及び基本原理) : 1996が,この国際規格と一致している。
(3) ISO 10303-11 : 1994 Industrial automation systems and integration−Product data representation and
exchange−Part 11 : Description methods : The EXPRESS language reference manual
備考 JIS B 3700-11(産業オートメーションシステム及びその統合−製品データの表現及び交換−
第11部:記述法:EXPRESS言語) : 1996が,この国際規格と一致している。
(4) ISO 10303-41 : 1994 Industrial automation systems and integration−Product data representation and
exchange−Part 41 : Integrated generic resources : Fundamentals of product description and support
備考 JIS B 3700-41(産業オートメーションシステム及びその統合−製品データの表現及び交換−
第41部:統合総称リソース:製品記述の基本要素) : 1996が,この国際規格と一致し
ている。
(5) ISO 10303-43 : 1994 Industrial automation systems and integration−Product data representation and
exchange−Part 43 : Integrated generic resources : Representation structures
備考 JIS B 3700-43(産業オートメーションシステム及びその統合−製品データの表現及び交換−
第43部:統合総称リソース:表現構造) : 1996が,この国際規格と一致している。
4
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3. 定義,記号及び略号
3.1
定義 この規格では,次の用語を定義する。
3.1.1
弧状連結 (arcwise connected) あるエンティティの定義域の中にある任意の2点が,定義域内に完
全に収まる曲線で連結されること。
3.1.2
軸対称 (axi-symmetric) あるエンティティが対称軸をもち,その軸まわりの回転について不変で
あること。
3.1.3
位相境界,境界 (bound) ある位相エンティティの限界を示す,より低い次元数の位相エンティテ
ィ。面の境界はループとし,稜線の境界は頂点とする。
3.1.4
幾何境界,境界 (boundary) Rm空間に含まれる定義域Xの境界とは,次の性質をもつ点xの集合。
xを含むRmの開球Uのうち,UとXとの積U∩Xがd次元(d≦m)の閉半空間
d
R+ における開集合に位相
同型であるものが存在する。このときxは,
d
R+ の原点に対応する。
備考1.
d
R+ は,x1≧0であるRdのすべての数学的な点(x1,x2,…,xd)の集合であると定義す
る。
2. このため,用語“開”は,通常の数学的な意味をもつ。この規格の他の箇所で定義され
ている“開曲面”とは関係ない。
3.1.5
境界表現立体モデル (boundary representation solid model, B-rep) 形状モデルの一種であって,立
体の寸法及び形状が,その境界を構成する面,稜線及び頂点によって定義されるもの。
3.1.6
閉曲線 (closed curve) 両方の端点が同一である曲線。
3.1.7
閉曲面 (closed surface) 連結2-多様体であり,3次元空間をちょうど二つの連結構成要素に分割す
るもの。分割された空間の一方は,有限とする。
3.1.8 位相エンティティの完備集合 (completion of a topological entity) 対象とする位相エンティティと,
その境界の定義において直接的又は間接的に参照されるすべての面,稜線及び頂点とからなる集合。
3.1.9
連結 (connected) 弧状連結(3.1)に同じ。
3.1.10 連結構成要素 (connected component) 定義域の極大連結部分集合。
3.1.11 CSG (constructive solid geometry) 形状モデル表現の一種。立体モデルに対する一連の正規化ブー
ル操作の結果として,立体が定義される。
3.1.12 座標空間 (coordinate space) n次元空間の各点に,n個のパラメタからなる集合を一意に関連付け
る参照系。
3.1.13 曲線 (curve) 実数直線(R1)の連結部分集合上で定義される連続関数の2次元又は3次元空間に
おける像であって,単独の点ではない数学的な点の集合。
3.1.14 サイクル (cycle) グラフにおける頂点と稜線とが交互に現れる連鎖であって,最初及び最後の頂
点が同じもの。
3.1.15 境界付きd-多様体 (d-manifold with boundary) d次元内部と境界との和からなる定義域。
3.1.16 次元数 (dimensionality) 幾何エンティティのパラメタ空間における独立した座標の数。定義域を
もつ必要のない位相エンティティの次元数は,エンティティ定義で指定される。リスト又は集合の次元数
は,リスト又は集合の要素の次元数の最大値とする。
3.1.17 定義域 (domain) エンティティに対応するモデル空間内の数学的な点の集合。
5
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.1.18 オイラー式 (euler equation) モデルの位相の整合性を検証するために使用する方程式。エンティ
ティの位相的な性質を関係付ける種々の等式は,オイラー (euler) の標数として知られる数の不変性から
導かれる。これらの等式は,位相構造の整合性を高速に検査するときに,よく用いられる。オイラー式の
条件を満足しない場合は,“あり得ない”モデルであると認識できる。この規格では,次の特別な二つの場
合を重要視する。グラフに対するオイラー式は5.2.3,曲面に対するオイラー式の条件は5.4.23及び5.4.25
による。
3.1.19 大きさ (extent) エンティティの定義域の内容の測度。この側度は,エンティティの次元数に応じ
た単位で測られる。すなわち,次元数が1,2及び3に対して,それぞれ長さ,面積及び体積が用いられる。
必要な場合,記号Ξで大きさを示す。
3.1.20 有限 (finite) エンティティについて有限な上界が存在して,その定義域にある任意の二つの点の
距離が,その上界以下であること。
3.1.21 グラフの種数 (genus of a graph) グラフ通過アルゴリズム(5.2.3備考参照)によって手続き的に
定義される整数値の不変量。
3.1.22 曲面の種数 (genus of a surface) 対象とする曲面に位相同型な曲面を生成するために,球面に加え
なければならないハンドルの個数。
3.1.23 幾何的に基礎付けられた (geometrically founded) geometric̲representation̲itemの特性であって,
座標空間との関係が示されていること。この座標空間において,geometric̲representation̲itemの位置及び
向きを表す点及び方向の座標値が定義される。
3.1.24 幾何的に関係付けられた (geometrically related) 同一のcontextに結合された二つの
geometric̲representation̲itemの関係であって,これによって両者間の距離及び方向の概念が定義される。
3.1.25 幾何座標系 (geometric coordinate system) すべての幾何が参照する大域的な直交デカルト座標系。
3.1.26 グラフ (graph) 頂点及び稜線の集合。この規格で対象とするグラフは,自己ループと,同一の2
頂点を接続する多重稜線とを許すので,技術文献では,通常,疑似グラフと呼ばれる。
3.1.27 ハンドル (handle) 輪環体を球面から区別する構造。これは,曲面における二つの穴を結ぶ円柱状
の管とみなすことができる。
3.1.28 位相同型 (homeomorphic) 定義域XからYへ一対一対応する連続関数f-が存在し,逆関数f-−1が
連続であること。
3.1.29 内側 (inside) 定義域Xが定義域Yの内側にあるとは,定義域XとYが同一のユークリッド空間
Rmに含まれ,YがRmをちょうど二つの連結構成要素に分け,その一つが有限であり,Xが有限の構成要素
に含まれること。
3.1.30 内部 (interior) Rmに含まれるd次元定義域Xのd次元内部とは,Xにおいて次の性質をもつ点x
の集合。xを含むRmの開球Uのうち,UとXとの積U∩XがRdの開球と位相同型になるものが存在する。
3.1.31 リスト (list) 順序付けされた同じ型の集まり。要素は,重複してもよい。リストは, [A] のよう
に角括弧でくくって表現する。
3.1.32 モデル空間 (model space) 実在の物体の幾何が定義される,次元数が2又は3の空間。
3.1.33 開曲線 (open curve) 二つの異なる端点をもつ曲線。
3.1.34 開曲面 (open surface) 境界をもつ多様体であって,閉じていない曲面。すなわち,有限でないか,
又は空間をちょうど二つの連結構成要素に分割しないかのいずれかとする。
3.1.35 向き付け可能 (orientable) 曲面の法線ベクトルの向きが,連続的に変化し整合性をもつこと。
備考 これは,法線ベクトルの値が連続的に変化することを要求しない。曲面には,接平面の不
6
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
連続性があってもよい。
3.1.36 干渉 (overlap) 二つのエンティティがシェル,面,稜線又は頂点を共有すること。
3.1.37 パラメタ範囲 (parameter range) 曲線又は曲面の有効なパラメタ値の範囲。
3.1.38 パラメタ空間 (parameter space) 一意に定義されたパラメタ化によって,曲線に関連付けられた1
次元空間,又は曲面に関連付けされた2次元空間。
3.1.39 配置座標系 (placement coordinate system) 空間中の幾何エンティティの配置を示すための直交デ
カルト座標系。属性の解釈の記述と,曲線エンティティ及び曲面エンティティの一意なパラメタ化の定義
とに用いる。
3.1.40 自己干渉 (self-intersect) 曲線又は曲面の場合,パラメタ範囲内にある少なくとも二つの点の像で
ある数学的な点がその定義域に存在し,かつこれら二つの点の一つがパラメタ範囲の内部にあること。頂
点,稜線又は面の場合,その定義域において自己干渉すること。
備考 曲線又は曲面は,それが閉じているだけでは自己干渉しているとは見なさない。
3.1.41 自己ループ (self-loop) 両端が同一の頂点である稜線。
3.1.42 集合 (set) 重複する要素がなく,かつ順序付けのない集まり。
3.1.43 空間次元数 (space dimensionality) 座標空間の点の配置を定義するために必要なパラメタの数。
3.1.44 曲面 (surface) 平面(R2)の連結部分集合上で定義される連続関数の像である数学的な点の集合。
3.1.45 位相上の向き (topological sense) 属性の順序から導かれる位相エンティティの向き。
例1. 稜線の位相上の向きは,稜線の開始頂点から終了頂点への方向とする。
例2. 稜線列の位相上の向きは,リストの順に並べた稜線の順番に従う。
3.2
記号 (Symbol) この規格では,次の記号を使用する。
3.2.1
幾何に関する数学記号 幾何スキーマで使用する数学記号の用法は,表1のとおりとする。
表1 幾何に関する数学記号
記号
定義
α
スカラ量
A
ベクトル量
<>
ベクトルの正規化
a
正規化されたベクトル(例えは,a=<A>=A/|A|)
×
外積
・
内積
A→B
AからBへの変換
λ(u)
パラメタ曲線
C(x, y, z)
解析曲線
σ(u, v)
パラメタ曲面
S(x, y, z)
解析曲面
Cx
xに関するCの偏微分
σu
uに関するσ(u,v)の偏微分
Sx
xに関するSの偏微分
||
絶対値,大きさ又は行列式
Rm
m次元実空間
3.2.2
位相に関する記号 位相エンティティが満たさなければならない制約を厳密に定義する試みがな
されてきた。多くの場合,これらは,記号的に定義されている。ここでは,この目的のために使用する表
記法について定義する。ここでの定義は,EXPRESSの定義又は用法とは無関係とする。
位相的な構成要素は,vertex, edge, path, loop, face(及びsubface)並びにshellとする。これらは,それぞ

7
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
れ記号V, E, P, L, F及びSによって参照される。
これらのエンティティの幾つかは,特別な形式をとるが,形式の区別をするために,必要に応じて上付
き添字を用いる。
例3. loopは,vertex̲loop,edge̲loop又はpoly̲loopのいずれかである。これらはLv,Le又はLp
と表す。
表2に位相スキーマで使用する記号の一覧を示す。
表2 位相に関する記号
記号
定義
V
ν
vertex
一意なvertexの数
E
ε
El
εl
Ge
方向のないedge
一意な方向のないedgeの数
oriented̲edge
一意なoriented̲edgeの数
edgeの種数
P
P
Gp
path
一意なpathの数
pathの種数
L
L
Ll
Ll
Le
Lp
Lv
Gl
loop
一意なloopの数
face̲bound
一意なface̲boundの数
edge̲loop
poly̲loop
vertex̲loop
loopの種数
F
F
Hf
face
一意なfaceの数
faceの種数
S
S
Sc
So
Sv
Sw
Hs
shell
一意なshellの数
closed̲shell
open̲shell
vertex̲shell
wire̲shell
shellの種数
Ξ
大きさ
{A}
[A]
型Aのエンティティの集合
型Aのエンティティのリスト
方向のないedgeは,下位型のoriented̲edgeではないエンティティedgeとする。エンティティ定義の幾
つかにおいては,位相の属性は(位相+論理)の対の形式をとることがあり,その場合,一般に下位型の
oriented̲xxxのような名前のエンティティで表現される。位相の場合と(位相+論理)の対の場合とを区別
するために,例えば,EとEl,Soと
olSなどのように下付き添字を用いる。
幾つかの位相エンティティは,参照されるエンティティの方向が参照するエンティティの方向と同じか
反対かを示すために,向きフラグを用いる。フラグがTRUEの場合,参照されるエンティティの方向は同
じとし,FALSEの場合は,参照されるエンティティの方向は(概念的には)反対とする。上位で参照する
8
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
エンティティから下位で参照されるエンティティへと連鎖する場合,複数の向きフラグか存在しうる。上
位で参照するエンティティの方向に対して下位で参照されるエンティティの方向は,向きフラグの連鎖の
一致論理(not exclusive or, ◯
・)を評価することで得られる。例えば,faceは(loop+Loop向きフラグ)を
参照し,loopは(edge+Edge向きフラグ)を参照し,edgeは(curve+Curve向きフラグ)を参照する。face
の“FaceCurve向きフラグ”は,次の式で与えられる。
FaceCurve向きフラグ=Loop向きフラグ◯
・Edge向きフラグ◯
・Curve向きフラグ
ここで,一致論理は,二つのフラグが同じ値をもつときTRUEとする。更に,次の真理値表によって定義
される。
T◯
・T=T
T◯
・F=F=F◯
・T
F◯
・F=T
したがって,次のとおりとなる。
F◯
・T◯
・F=T
3.3
略語 この規格では,次の略語を用いる。
B-rep boundary representation solid model
CSG constructive solid geometry
4. 幾何 (Geometry) 次のEXPRESS宣言は,geometry̲schemaを開始し,必要な外部参照を明らかにす
る。
EXPRESSによる定義
*)
SCHEMA geometry̲schema;
REFERENCE FROM representation̲schema
(representation,
functionally̲defined̲transformation,
representation̲item,
representation̲context,
definitional̲representation,
item̲in̲context,
using̲representations);
REFERENCE FROM measure̲schema
(length̲measure,
positive̲length̲measure,
plane̲angle̲measure,
plane̲angle̲unit,
positive̲plane̲angle̲measure,
parameter̲value,
global̲unit̲assigned̲context);
REFERENCE FROM topology̲schema
(edge̲curve,
9
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
face̲surface,
poly̲loop,
vertex̲point);
REFERENCE FROM geometric̲model̲schema
(solid̲model,
boolean̲result,
sphere,
right̲circular̲cone,
right̲circular̲cylinder,
torus,
block,
right̲angular̲wedge,
half̲space̲solid,
shell̲based̲surface̲model,
face̲based̲surface̲model,
shell̲based̲wireframe̲model,
edge̲based̲wireframe̲model,
geometric̲set);
(*
備考1. 上で参照しているスキーマは,次の規格による。
representation̲schema
JIS B 3700-43
measure̲schema
JIS B 3700-41
topology̲schema
この規格の5.
geometric̲model̲schema この規格の6.
2. topology̲schema及びgeometric̲model schemaへの参照は,上位型geometric̲representation̲item
の定義のためだけに必要とする。
3. このスキーマの図式表現を附属書Dの図D.1〜D.12に示す。
4.1
概要 geometry̲schemaの主題は,パラメタ曲線及びパラメタ曲面の幾何とする。
representation̲schema(JIS B 3700-43参照)及びこの規格で定義するgeometric̲representation̲contextは,
幾何を定義するコンテキストを提供する。それによって,幾何的に関係付けられる要素と独立した座標空
間に存在する要素とを区別することが可能となる。特に,各geometric̲representation̲itemは,その座標空
間のユークリッド次元を属性として含むgeometric̲representation̲contextをもつ。ここでは,その空間の座
標系を幾何座標系と呼ぶ。length̲measure及びplane̲angle̲measureの単位は,このコンテキストの中で大
域的に決められているとする。規則 (compatible̲dimension) によって,同じgeometric̲representation̲context
の中では,すべてのgeometric̲representation̲itemが同一の空間次元数をもつことか保証される。空間次元
数dimは,geometric̲representation̲itemのすべての下位型に継承される誘導属性とする。
4.2
基本概念及び前提条件
10
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.2.1
空間次元数 すべての幾何は,各軸の単位が同一の右手系の直交デカルト座標系において定義され
る。2次元及び3次元のいずれの幾何の定義にも共通な枠組を用いる。point及びdirectionのいずれにも,
2次元及び3次元の形式が存在し,これらの形式は,単に3番目の座標値があるかないかによって区別さ
れる。複雑な幾何エンティティは,すべてpoint及びdirectionを用いて定義され,それらから空間次元数
が導出される。
4.2.2
幾何的関係 一つのgeometric̲representation̲contextをもつrepresentationにitemsとして含まれてい
るすべてのgeometric̲representation̲itemは,幾何的に関係付けられている。このとき
geometric̲representation̲itemは,そのrepresentationのコンテキストにおいて幾何的に基礎付けられている
と言う。異なるrepresentationにitemsとして現れるgeometric̲representation̲itemに対しては,幾何的関係
(例えば点と点との間の距離)は,存在しない。
4.2.3
解析曲線及び解析曲面のパラメタ化 ここで定める曲線及び曲面には,それぞれパラメタ化が定義
されている。幾つかの曲線や曲面は,本来,パラメタを用いて定義される。一方,円錐曲線及び初等曲面
は,幾何的に定義される。
後者の場合,パラメタ化の定義に配置座標系を用いる。幾何的な定義は,パラメタ化に必要なデータを
一部含んでいるが,すべてではない。配置座標系を定義するデータは,個々の曲線エンティティ又は曲面
エンティティと結合したaxis2̲placementに含まれる。
4.2.4
曲線 4.4で定義する曲線エンティティは,直線,初等円錐曲線,一般的なパラメタ多項式曲線及
び参照によって又は手続き的に定義された曲線とする。すべての曲線は,曲線をトリム (trim) したり,パ
ラメタ値によって曲線上の点が区別されるように,パラメタ化される。円錐曲線に対しては,空間中の向
き及び位置から幾何形式を分離した表現方法を用いている。いずれの場合でも,向き及び位置の情報は,
エンティティaxis2̲placementによって表す。はん(汎)用のパラメタ曲線は,エンティティb̲spline̲curve
を用いて表現する。これは,すべての型の多項式及び有理パラメタ式の曲線のデータ交換に対する最も安
定した表現形式として選ばれた。適当な属性値及び下位型を用いれば,エンティティb̲spline̲curveは,
多項式,有理式,ベジエ形式又はB-スプライン形式のスプライン曲線を表現できる。composite̲curveエン
ティティは,曲線をつなぐ点における連続性の情報を交換する仕組みをもち,より複雑な曲線を構成する。
offset̲curve及びcurve̲on̲surfaceは,他の幾何によって定義される曲線とする。offset̲curveには,2次
元及び3次元のアプリケーションに対して,別々のエンティティが存在する。curve̲on̲surfaceは,二つの
曲面の交差を表すintersection̲curveを含む。そのような曲線は,3次元空間中で表現しても,いずれかの
曲面の2次元パラメタ空間で表現してもよい。
4.2.5
曲面 曲面エンティティは,単純な境界表現 (B-rep) 立体モデリングシステムの要件を満たし,一
般的な多項式及び有理式パラメタ曲面のデータ交換を可能にする。単純な曲面とは,平面,球面,円柱面,
円錐面,輪環面,surface̲of̲revolution及びsurface̲of̲linear̲extrusionを指す。曲線の場合と同様,すべて
の曲面には,標準的なパラメタ化が存在する。多くの場合,曲面の定義には境界を含まない。すなわち,
曲面は,明示的に又は暗黙に境界があることを前提とする。明示的な境界は,rectangular̲trimmed̲surface
又はエンティティcurve̲bounded̲surfaceによって実現できる。暗黙的な境界は,faceを定義するための,
付加的な位相情報を結合することが必要となる。
エンティティb̲spline̲surface及びその下位型は,すべての型の多項式及び有理式の双パラメタ曲面のデ
ータ交換に対する,最も一般的な方法を与える。このエンティティは,曲面幾何を表現するのに最も安定
な形式として,制御点を用いる。エンティティoffset̲surfaceは,与えられた曲面に対し,単純に法線方向
へのオフセットを取って得られる曲面のデータ交換を目的とする。エンティティ
11
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
rectangular̲composite̲surfaceは,異なるsurface̲patchを接続した長方形状のメッシュを表現でき,その際,
surface̲patch間の連続性の次数を定義できる。
4.2.6
優先形式 幾つかの幾何エンティティでは,幾何的な対象を複数の方法で定義できる。このような
多重性には,“優先形式 (preferred form)”又は“主表現 (master representation)”を付ける。これは,パラメ
タ化を決定するために使われる形式とする。
備考 多重形式が実際に同一であることを保証するのは実用的ではないので,属性
master̲representationによって優先形式を指定できる。これは,恐らくデータの作成者によ
って決定されることになる。多重表現をもつエンティティに対して,パラメタ化,定義域
及び計算結果のような性質は,すべて主表現から導出される。他の表現を用いるのは,実
用性を考慮したための妥協である。
4.3
geometry̲schemaの型定義
4.3.1
dimension̲count dimension̲countは,geometric̲representation̲contextの座標空間次元数を定義す
るための正の整数とする。
EXPRESSによる定義
*)
TYPE dimension̲count = INTEGER;
WHERE
WR1: SELF > O;
END̲TYPE;
(*
形式的要件
WR1:dimension̲countは,正でなければならない。
4.3.2
transition̲code この型は,複合曲線又は複合曲面の連続性を表す。ここでの連続性とは,幾何の
性質であり,パラメタに関する性質ではない。
EXPRESSによる定義
*)
TYPE transition̲code = ENUMERATION OF
(discontinuous,
continuous,
cont̲same̲gradient,
cont̲same̲gradient̲same̲curvature);
END̲TYPE;
(*
列挙項目の定義
discontinuous:セグメント又はパッチが接続していない。曲線又は曲面が閉じていないことを示すために,
その境界においてだけ用いる。
continuous:セグメント又はパッチが接続しているが,接ベクトル又は法線ベクトルに関する条件は存在し
ない。
cont̲same̲gradient:セグメント又はパッチが接続していて,接ベクトル又は法線ベクトルが平行,かつ同
じ方向をもつ。導関数が一致する必要はない。
12
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
cont̲same̲gradient̲same̲curvature:曲線の場合,セグメントが接続していて,接ベクトルが平行,かつ同
じ方向をもち,更に曲率が等しい。導関数が一致する必要はない。曲面の場合,パッチの共通の境界に沿
って主曲率が等しく,主方向が一致している。
4.3.3
preferred̲surface̲curve̲representation この型は,surface̲curveに対する表現の優先形式を示す
ために用いられる。ここで,優先形式は,幾何空間における曲線又は基礎となる曲面上のパラメタ空間に
おける曲線のいずれかとする。
EXPRESSによる定義
*)
TYPE preferred̲surface̲curve̲representation = ENUMERATION OF
(curve̲3d,
pcurve̲s1,
pcurve̲s2);
END̲TYPE;
(*
列挙項目の定義
curve̲3d:3次元空間の曲線が優先される。
pcurve̲s1:1番目のpcurveか優先される。
pcurve̲s2:2番目のpcurveが優先される。
4.3.4
b̲spline̲curve̲form この型は,B-スプライン曲線 (b̲spline̲curve) で表される特定の形状を示す
ために使う。
EXPRESSによる定義
*)
TYPE b̲spline̲curve̲form = ENUMERATION OF
(polyline̲form,
circular̲arc,
elliptic̲arc,
parabolic̲arc,
hyperbolic̲arc,
unspecified);
END̲TYPE;
(*
列挙項目の定義
polyline̲form:次数1のB-スプライン基底関数によって表される直線セグメントのつながった並び。
circular̲arc:b̲spline̲curveで表される円弧又は円全体とする。
elliptic̲arc:b̲spline̲curveで表されるだ円弧又はだ円全体とする。
parabolic̲arc:b̲spline̲curveで表される放物線の有限の長さの弧とする。
hyperbolic̲arc:b̲spline̲curveで表される双曲線の一つの分岐の有限の長さの弧とする。
unspecified:特に形状を指定しないb̲spline̲curveとする。
4.3.5
b̲spline̲surface̲form この型は,B-スプライン曲面 (b̲spline̲surface) によって特定の形式の曲
面の一部を表現することを示すのに使われる。
13
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
TYPE b̲spline̲surface̲form = ENUMERATION OF
(plane̲surf,
cylindrical̲surf,
conical̲surf,
spherical̲surf,
toroidal̲surf,
surf̲of̲revolution,
ruled̲surf,
generalised̲cone,
quadric̲surf,
surf̲of̲linear̲extrusion,
unspecified);
END̲TYPE;
(*
列挙項目の定義
plane̲surf:各パラメタに関して,次数1のB-スプライン曲面で表される平面の境界付けられた部分。
cylindrical̲surf:円柱面の境界付けられた部分。
conical̲surf:直円錐面の曲面の境界付けられた部分。
spherical̲surf:b̲spline̲surfaceで表される球面の境界付けられた部分又は球面全体。
toroidal̲surf:b̲spline̲surfaceで表される輪環体又は輪環体の部分。
surf̲of̲revolution:回転面の境界付けられた部分。
ruled̲surface:二つのパラメタ曲線上の,同じパラメタ値に対応する点を直線で結んで作られる曲面。
generalised̲cone:第二の曲線が一点に縮退した線織面の特別な場合。b̲spline̲surfaceで表すとき,一つの
稜線に沿ったすべての制御点は一致する。
quadric̲surf:変数x,y及びzに関して次数2の曲面のクラスに属する境界付けられた部分とする。
surf̲of̲linear̲extrusion:パラメタのうちの一つに関して次数1のb̲spline̲surfaceで表される
surface̲of̲linear̲extrusionの境界付けられた部分。
unspecified:特に形を指定しない曲面とする。
4.3.6
knot̲type この型は,B-スプラインのノット (knot) が暗黙に定められるような,特に簡単な形式
をとることを示す。これらの型の解釈の詳細は,B-スプライン曲線エンティティの定義(4.4.29参照)に
よる。
EXPRESSによる定義
*)
TYPE knot̲type = ENUMERATION OF
(uniform̲knots,
unspecified,
quasi̲uniform̲knots,
piecewise̲bezier̲knots);
14
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲TYPE;
(*
列挙項目の定義
uniform̲knots:一様B-スプライン曲線に適合するノットの形式。
unspecified:ノットの型は,規定しない。非一様ノットの場合を含む。
quasi̲uniform̲knots:準一様B-スプライン曲線に適合するノットの形式。
piecewise̲bezier̲knots:区分的ベジエ曲線に適合するノットの形式。
4.3.7
extent̲enumeration この型は,オブジェクトの定量的な大きさを規定するために用いる。
EXPRESSによる定義
*)
TYPE extent̲enumeration = ENUMERATION OF
(invalid,
zero,
finite̲non̲zero,
infinite);
END̲TYPE;
(*
列挙項目の定義
invalid:大きさの概念が計測される量に関して有効でない。
zero:大きさが0とする。
finite̲non̲zero:大きさは有限(有界)であるか,0ではない。
infinite:大きさが有限でない。
4.3.8
trimming̲preference この型は,パラメタ曲線のトリムの方法が多重に定義されている場合,優先
されるトリムの方法の方法を示す。
EXPRESSによる定義
*)
TYPE trimming̲preference = ENUMERATION OF
(cartesian,parameter,
unspecified);
END̲TYPE;
(*
列挙項目の定義
cartesian:cartesian̲pointによるトリムの方法が優先される。
parameter:parameter̲valueが優先される。
unspecified:優先される方法が指定されていない。
4.3.9
axis2̲placement この選択型は,2次元又は3次元のデカルト空間で使われる2種類の
axis2̲placementからなる。これによって,配置に関する情報を必要とするエンティティは,空間次元数を
指定せずに参照できる。
EXPRESSによる定義
*)
15
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TYPE axis2̲placement = SELECT
(axis2̲placement̲2d,
axis2̲placement̲3d);
END̲TYPE;
(*
4.3.10 curve̲on̲surface curve̲on̲surfaceは,パラメタ曲面上の曲線であり,次のどれであってもよい。
− pcurve
− surface̲curve(intersection̲curve及びseam̲curveの特別な下位型を含む。)
− composite̲curve̲on̲surface
curve̲on̲surface選択型は,参照を目的としてこれらの曲線を集めたものとする。
EXPRESSによる定義
*)
TYPE curve̲on̲surface = SELECT
(pcurve,
surface̲curve,
composite̲curve̲on̲surface);
END̲TYPE;
(*
4.3.11 pcurve̲or̲surface この選択型によって,エンティティsurface̲curveが,結合されるsurface又は
pcurveを一つの属性として表す。
EXPRESSによる定義
*)
TYPE pcurve̲or̲surface = SELECT
(pcurve,
surface);
END̲TYPE;
(*
4.3.12 trimming̲select この選択型は,パラメタ曲線をトリムする二つの可能な方法を示す。それらは,
曲線上のcartesian̲pointである点による方法か,又は曲線のパラメタ範囲のパラメタ値を定義する実数に
よる方法のいずれかとする。
EXPRESSによる定義
*)
TYPE trimming̲select = SELECT
(cartesian̲point,
parameter̲value);
END̲TYPE;
(*
4.3.13 vector̲or̲direction この型は,ベクトルの計算に使用できるエンティティの型を示す。
EXPRESSによる定義
*)
16
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TYPE vector̲or̲direction = SELECT
(vector,
direction);
END̲TYPE;
(*
4.4
geometry̲schemaのエンティティ定義 ここでは,すべての明示的幾何エンティティを定義する。
パラメタ空間で定義されているエンティティを除き,すべての幾何は,右手系のデカルト座標系(幾何座
標系)で定義する。この座標系の空間次元数は,geometric̲representation̲itemのコンテキストで決まる。
曲線及び曲面の定義は,本質的にはすべて点,ベクトル及び/又はスカラ値(長さ)によって与える。
4.4.1
geometric̲representation̲context geometric̲representation̲contextは,geometric̲representation̲item
が幾何的に基礎付けられているrepresentation̲contextとする。
geometric̲representation̲contextは,独立した座標空間なので,特に適当な変換によって関係付けられる
場合を除いて,他の座標空間には,空間的に関係付けられていない(幾何的な基礎付け及び座標空間の定
義については,3.1参照)。
EXPRESSによる定義
*)
ENTITY geometric̲representation̲context
SUBTYPE OF (representation̲context);
coordinate̲space̲dimension : dimension̲count;
END̲ENTITY;
(*
属性定義
coordinate̲space̲dimension:geometric̲representation̲contextである座標空間のdimension̲count。
備考 coordinate̲space̲dimensionの許されている範囲に対する制約は,この規格の範囲外とする。
4.4.2 geometric̲representation̲item geometric̲representation itemは,付加的な意味として幾何的な位置,
向き又はその両方をもつrepresentation̲itemとする。この意味は,次のいすれかによって表現される。
− cartesian̲point又はdirectionとする。
− cartesian̲point又はdirectionを直接的に参照する。
− cartesian̲point又はdirectionを間接的に参照する。
備考1. cartesian̲point又はdirectionを間接的に参照するとは,あるgeometric̲representation̲itemが一
つ以上の介在する属性を通じてcartesian̲point又はdirectionを参照することとする。多くの
場合,この情報は,axis2̲placementの形で与える。
例4. 円を考えた場合,それはaxis2̲placementを参照することによって,幾何的な位置及び
向きをもつ。axis2̲placementは,一つのcartesian̲point及び幾つかのdirectionを参照
する。
例5. manifold̲solid̲brepは,topological̲representation̲itemの幾つかの階層を通じてcurve,
sur-face及びpointを参照するgeometric̲representation̲itemとする。そして,曲線及び
曲面は,付加的なエンティティを介してcartesian̲point及びdirectionを参照する。
2. 介在するエンティティは,すべてrepresentation̲itemであるか,下位型
geometric̲representation̲itemである必要はない。上のmanifold̲solid̲brepの例では,介在する
17
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
representation̲itemの階層の一つは,closed̲shellとする。これは,topological̲representation̲item
であって,それ自体としてはgeometric̲representation̲contextを必要としない。closed̲shellは,
それ自体がgeometric̲representation̲itemであるmanifold̲solid̲brepの定義の一部として使わ
れた場合,geometric̲representation̲contextに基礎付けられる。
3. geometric̲representation̲itemは,representation内のrepresentation̲contextに関係付けられる必
要性を継承する。compatible̲dimension
規則は,representation̲context
が
geometric̲representation̲con-textであることを保証している。幾何のコンテキストの中で,こ
の関係によって,geometric̲repre-sentation̲itemは,幾何的に基礎付けられる。
EXPRESSによる定義
*)
ENTITY geometric̲representation̲item
SUPERTYPE OF (ONEOF(point, direction, vector, placement,
cartesian̲transformation̲operator, curve, surface,
edge̲curve, face̲surface, poly̲loop, vertex̲point,
solid̲model, boolean̲result, sphere, right̲circular̲cone,
right̲circular̲cylinder, torus, block,
right̲angular̲wedge, half̲space̲solid,
shell̲based̲surface̲model, face̲based̲surface̲model,
shell̲based̲wireframe̲model, edge̲based̲wireframe̲model,
geometric̲set))
SUBTYPE OF (representation̲item);
DERIVE
dim : dimension̲count := dimension̲of(SELF);
WHERE
WR1: SIZEOF (QUERY (using̲rep <* using̲representations (SELF) |
NOT ('GEOMETRY̲SCHEMA, GEOMETRIC̲REPRESENTATION̲CONTEXT' IN
TYPEOF (using̲rep, context̲of̲items)))) =O;
END̲ENTITY;
(*
属性定義
dim:geometric̲representation̲itemの座標のdimension̲count。
備考1. 属性dimは,そのgeometric̲representation̲itemが幾何的に基礎付けられている
geometric̲representation̲contextのcoordinate̲space̲dimensionから導出される。
2. geometric̲representation̲itemは,すべてが同じcoordinate̲space̲dimensionをもつ,一つ以上
のgeometric̲representation̲contextにおいて幾何的に基礎付けられているとする。4.5.1の
compatible̲dimension規則を参照する。
形式的要件
WR1:geometric̲representation̲item
を参照する表現のコンテキストは,すべて
geometric̲representation̲contextと同じ型でなければならない。
4.4.3
point point(点)は,実デカルト座標空間Rm(m=1,2又は3)における配置とする。
18
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
ENTITY point
SUPERTYPE OF (ONEOF (cartesian̲point, point̲on̲curve, point̲on̲surface,
point̲replica, degenerate̲pcurve))
SUBTYPE OF (geometric̲representation̲item);
END̲ENTITY;
(*
4.4.4
cartesian̲point cartesian̲pointは,直交デカルト座標系又はパラメタ空間における座標によって定
義されるpointとする。このエンティティは,1〜3次元の空間中で定義され,その次元数は,リスト
coordinatesの要素数で示される。
備考 この規格では,幾何を定義する目的として2次元又は3次元の点だけを使う。
EXPRESSによる定義
*)
ENTITY cartesian̲point
SUBTYPE OF (point);
coordinates : LIST [1:3]OF length̲measure;
END̲ENTITY;
(*
属性定義
coordinates[1]:pointの配置の第1座標。
coordinates[2]:pointの配置の第2座標,1次元の点の場合には存在しない。
coordinates[3]:pointの配置の第3座標,1次元又は2次元の点の場合には存在しない。
SELF\geometric̲representation̲item.dim:pointが定義されている空間の次元数。これは
geometric̲representation̲itemの上位型から継承される誘導属性であって,cartesian̲pointに対してはリスト
coordinatesの要素数によって定まる。
4.4.5
point̲on̲curve point̲on̲curveは,curve上にあるpointとする。pointは,特定のパラメタ値に対
するcurveを評価することによって定まる。pointの座標空間の次元数は,basis̲curveのそれと同じとする。
EXPRESSによる定義
*)
ENTITY point̲on̲curve
SUBTYPE OF (point);
basis̲curve : curve;
point̲parameter
: parameter̲value;
END̲ENTITY;
(*
属性定義
basis̲curve:point̲parameterが関係しているcurve。
point̲parameter:pointの配置のパラメタの値。
SELF\geometric̲representation̲item.dim:point̲on̲curveが定義される空間の次元数。これはbasis̲curveの
19
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
それと同じとする。
非形式的要件
IP1:point̲parameterの値は,curveのパラメタ範囲外であってはならない。
4.4.6
point̲on̲surface point̲on̲surfaceは,パラメタ曲面であるsurfaceの上にあるpointとする。point
は,特定のパラメタ値の組に対するsurfaceを評価することによって定義する。
EXPRESSによる定義
*)
ENTITY point̲on̲surface
SUBTYPE OF (point);
basis̲surface
: surface;
point̲parameter̲u : parameter̲value;
point̲parameter̲v : parameter̲value;
END̲ENTITY;
(*
属性定義
basis̲surface:パラメタ値が関係しているsurface。
point̲parameter̲u:pointの配置の最初のパラメタ値。
point̲parameter̲v:pointの配置の2番目のパラメタ値。
SELF\geometric̲representation̲item.dim:point̲on̲surfaceの座標空間の次元数。
basis̲surfaceのそれと同じとする。
非形式的要件
IP1:u及びvとして指定されるパラメタ値は,basis̲surfaceのパラメタ範囲外であってはならない。
4.4.7
point̲replica これは,異なる配置に存在するpoint(親)の複製(replica)を定義する。複製は,
親のpointと同じ座標空間の次元数をもつ。
EXPRESSによる定義
*)
ENTITY point̲replica
SUBTYPE OF (point);
parent̲pt : point;
transformation : cartesian̲transformation̲operator;
WHERE
WR1: transformation.dim = parent̲pt.dim;
WR2: acyclic̲point̲replica (SELF,parent̲pt);
END̲ENTITY;
(*
属性定義
parent̲pt:複製されるpoint。
transformation:point̲replicaの配置を定義するcartesian̲transformation̲operator。
形式的要件
WR1:変換属性の座標空間の次元数は,parent̲ptのそれと一致しなければならない。
20
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WR2:point̲replicaは,それ自身の定義に用いてはならない。
4.4.8
degenerate̲pcurve degenerate̲pcurveは,pcurveの構造をもつエンティティであるが,3次元モデ
ル空間で1点に縮退したものとする。そのために,これはcurveの下位型ではなく,pointの下位型とする。
備考 例えば,円錐の頂点は,degenerate̲pcurveとして表現することもできる。
EXPRESSによる定義
*)
ENTITY degenerate̲pcurve
SUBTYPE OF (point);
basis̲surface: surface;
reference̲to̲curve : definitional̲representation;
WHERE
WR1: SIZEOF(reference̲to̲curve\representation.items) = 1;
WR2: 'GEOMETRY̲SCHEMA.CURVE' IN TYPEOF
(reference̲to̲curve\representation.items[1]);
WR3: reference̲to̲curve\representation.
items[1]\geometric̲representation̲item.dim =2;
END̲ENTITY;
(*
属性定義
basis̲surface:そのパラメタ空間において,縮退した曲線が定義される曲面。
reference̲to̲curve:degenerate̲pcurveを定義するパラメタ空間曲線への関連付け。
形式的要件
WR1:reference̲to̲curveに対応するエンティティdefinitional̲representation内の要素の集合は,ちょうど一
つの要素をもたなければならない。
WR2:集合内の唯一の要素は,curveとする。
WR3:このパラメタ空間曲線の次元数は,2とする。
非形式的要件
IP1:モデル空間の曲線とみなせば,degenerate̲pcurveは,0の弧長をもたなければならない。
4.4.9
evaluated̲degenerate̲pcurve このエンティティは,degenerate̲pcurveを評価した結果を表現し,
それとcartesian̲pointとを関連付けする。
EXPRESSによる定義
*)
ENTITY evaluated̲degenerate̲pcurve
SUBTYPE OF (degenerate̲pcurve);
equivalent̲point : cartesian̲point;
END̲ENTITY;
(*
属性定義
equivalent̲point:degenerate̲pcurveで表現される幾何座標系内の点。
21
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.10 direction このエンティティは,2次元又は3次元の空間内の一般的な方向ベクトルを定義する。
ベクトルの成分の実際の大きさは,定義される方向には影響を与えず,x:y:z又はx:yの比だけが意味をも
つ。
備考 このエンティティの成分は,正規化されていない。単位ベクトルが必要な場合,使用される前
に正規化する必要がある。
EXPRESSによる定義
*)
ENTITY direction
SUBTYPE OF (geometric̲representation̲item);
direction̲ratios : LIST [2:3]OF REAL;
WHERE
WR1: SIZE0F(QUERY(tmp <* direction̲ratios | tmp <> 0.0)) > 0;
END̲ENTITY;
(*
属性定義
direction̲ratios[1]:X軸方向の成分。
direction̲ratios[2]:Y軸方向の成分。
direction̲ratios[3]:Z軸方向の成分。2次元の座標空間の場合は存在しない。
SELF\geometric̲representation̲item.dim:directionの座標空間の次元数。これは,上位型
geometric̲representation̲itemから継承された属性であり,このエンティティに対しては,リスト内の
direction̲ratiosリストの要素数字で定義される。
形式的要件
WR1:方向ベクトルの大きさは,0より大きくなければならない。
4.4.11 vector このエンティティは,方向及び大きさによってベクトルを定義する。属性magnitudeの値
は,ベクトルの大きさを定義する。
備考 ベクトルの大きさは,属性orientationの構成要素から計算してはならない。数値の不安定
性を減らすために,このような表現形式がとられている。例えば,大きさが2.0mmで各軸
と等しい角度を有するベクトルは,属性orientationを (1.0,1.0,1.0) として表現されること
もある。
EXPRESSによる定義
*)
ENTITY vector
SUBTYPE OF (geometric̲representation̲item);
orientation : direction;
magnitude : length̲measure;
WHERE
WR1: magnitude >=0.0;
END̲ENTITY;
(*
属性定義
22
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
orientation:vectorの方向。
magnitude:vectorの大きさ。magnitudeが0.0のvectorは,属性orientationにかかわらず,すべて値が同じ
とみなす。
SELF\geometric̲representation̲item.dim:vectorが定義される空間の次元数。
形式的要件
WR1:magnitudeは,正又は0でなければならない。
4.4.12 placement placementは,幾何のコンテキストの座標系に関して,幾何要素の配置を決める。これ
は定義される要素の配置を決め,下位型の場合は,その向きを与える。
EXPRESSによる定義
*)
ENTITY placement
SUPERTYPE OF (ONEOF(axis1̲placement,axis2̲placement̲2d,axis2̲placement̲3d))
SUBTYPE OF (geometric̲representation̲item);
location : cartesian̲point;
END̲ENTITY;
(*
属性定義
location:配置される要素の,例えば円の中心のような,参照点の幾何的な位置。
4.4.13 axis1̲placement 一つの軸の3次元空間における方向及び配置。axis1̲placementは,(上位型から
継承される)配置する点及び軸の方向によって定義される。軸の方向は,axisの方向又は (0.0,0.0,1.0) と
いう暗黙値のいずれかとする。このplacementの実際の方向は,誘導属性zによって与える。
EXPRIESSによる定義
*)
ENTITY axis1̲placement
SUBTYPE OF (placement);
axis : OPTIONAL direction;
DERIVE
z : direction : =NVL(normalise(axis), direction([0.0,0.0,1.0]));
WHERE
WR1: SELF\geometric̲representation̲item.dim = 3;
END̲ENTITY;
(*
属性定義
SELF\placement.location:軸上の参照点。
axis:局所的なZ軸の方向。
z:局所座標系におけるZ軸の方向を示す正規化されたdirection。
SELF\geometric̲representation̲item.dim:axis1̲placementの空間次元数で,そのlocationから決められ,常
に3とする。
形式的要件
WR1:座標空間の次元数は,3とする。
23
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.14 axis2̲placement̲2d 二つの互いに垂直な軸の2次元空間における配置及び向き。
axis2̲placement̲2dは,(上位型から継承される)点及び軸によって定義される。これは,2次元空間にお
けるオブジェクトの配置及び向きを決めるため,すなわち,配置座標系を定義するために用いられる。こ
のエンティティは,配置座標系の原点となる点を含む。配置座標系の定義を完全にするために,方向ベク
トルが必要となる。ref̲directionは,配置座標系X軸の方向を定義する。配置座標系Y軸の方向は,それ
から導出される。
EXPRESSによる定義
*)
ENTITY axis2̲placement̲2d
SUBTYPE OF (placement);
ref̲direction : OPTIONAL direction;
DERIVE
p : LIST [2:2]OF direction : = build̲2axes(ref̲direction);
WHERE
WR1:SELF\geometric̲representation̲item.dim = 2;
END̲ENTITY;
(*
属性定義
SELF\placement.location:結合された配置座標系の原点を定義する参照点の空間的な位置。
ref̲direction:局所座標系X軸の方向を定めるためのdirection。ref̲directionが省略された場合,この方向
は,幾何座標系から決める。
p:配置座標系のための軸の集合。
p[1]:配置座標系におけるX軸の方向を示す正規化されたdirection。ref̲directionが省略された場合は,
(1.0,0.0) とする。
p[2]:配置座標系におけるY軸の方向を示す正規化されたdirection。これは,誘導属性であってp[1]と直
交する。
形式的要件
WR1:axis2̲placement̲2dの空間次元数は,2とする。
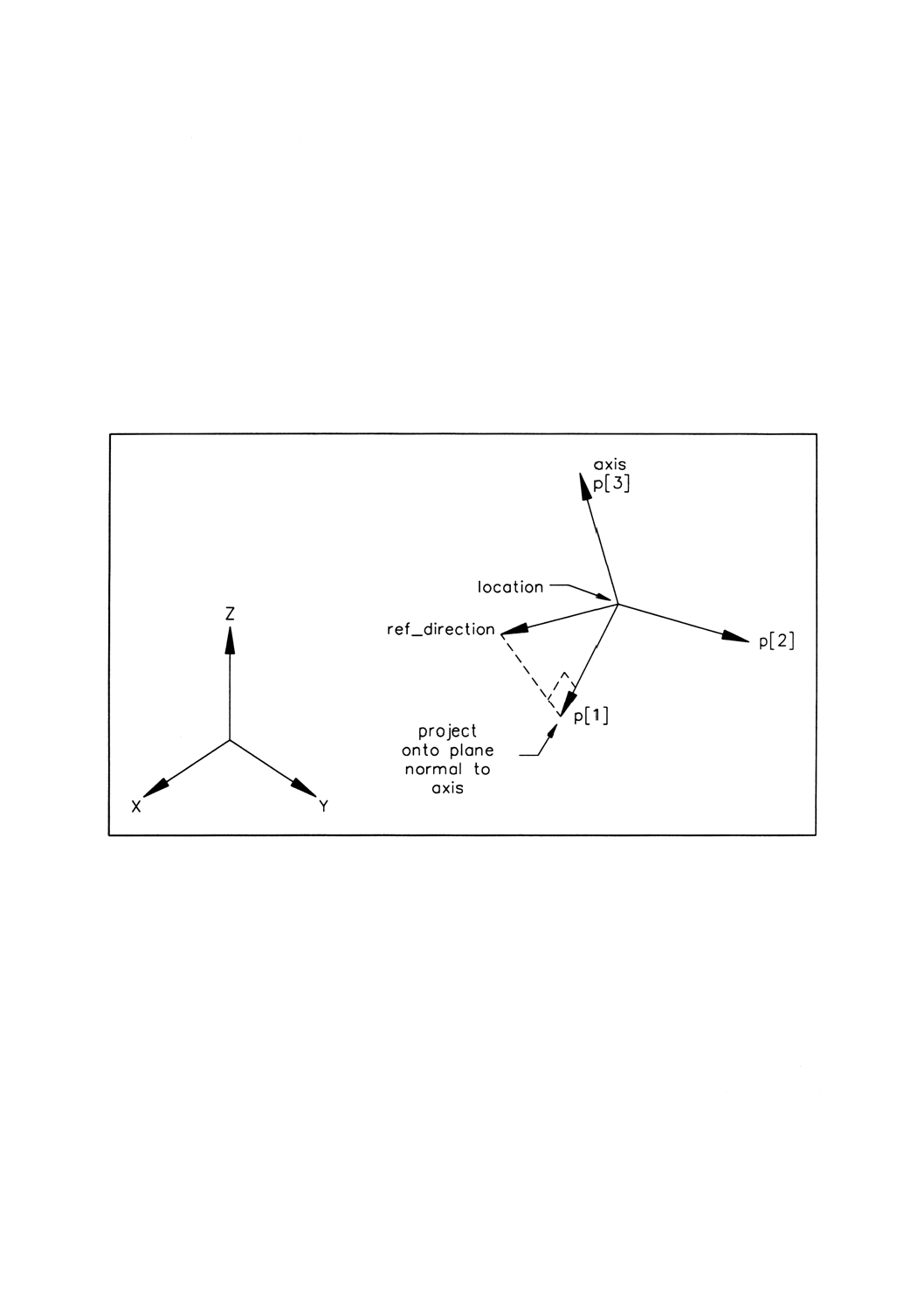
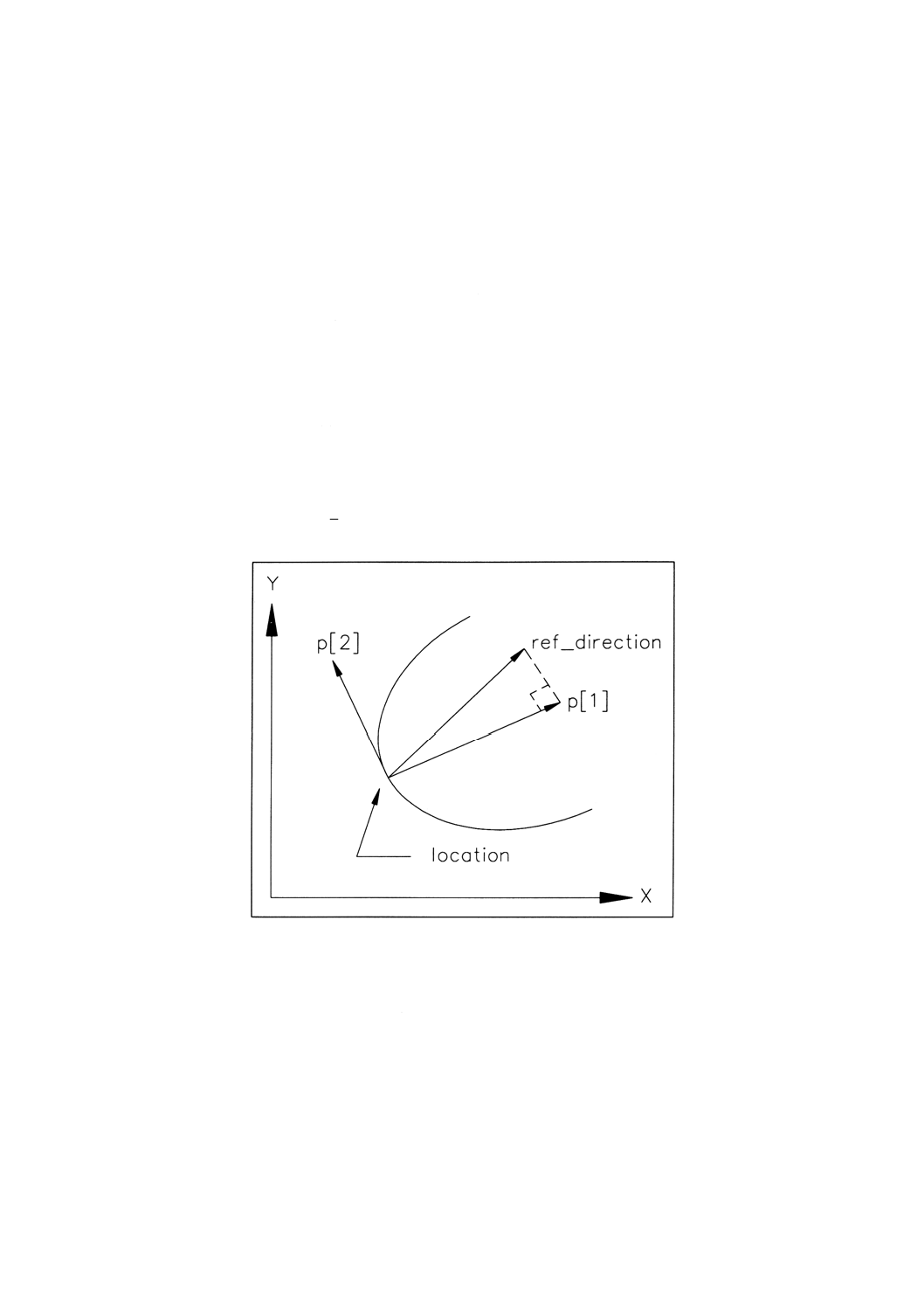
4.4.15 axis2̲placement̲3d 二つの互いに垂直な軸の3次元空間における配置及び向き。
axis2̲placement̲3dは,(上位型から継承される)点及び(理想的には直交している)二つの軸によって定
義される。これは,空間内の軸対称でないオブジェクトの配置及び向きを決めるため,すなわち,配置座
標系を定義するために用いることができる。このエンティティは,配置座標系の原点となる点を含む。配
置座標系の定義を完全にするために,二つの方向ベクトルが必要となる。axisは,配置座標系のZ軸方向
とし,ref̲directionは,配置座標系のX軸方向の近似とする。
備考 zを配置座標系のZ軸方向,aを配置座標系のX軸方向の近似とする。配置座標系のX軸
及びY軸の方向を計算するために,二つの方法がある。これらは,数学的には同じである
が,数値的には異なることもある。
(a) 配置座標系のX軸の方向をx=<a−(a・z)z>として与える。このとき,ベクトルaは,
原点P及びベクトルzで定義される平面に投影される。配置座標系のY軸の方向をy=
<z×x>で与える。
24
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(b) 配置座標系のY軸の方向をy=<z×a>として求め,次に配置座標系のX軸の方向を
x=<y×z>で与える。
数値的に,より安定している可能性が高いことから,二つのうち,最初の方法を使用す
る。
円錐曲線及び初等曲面に関しては,パラメタ式によって参照される配置座標系は,axis2̲placement̲3d
から導かれる。
EXPRESSによる定義
*)
ENTITY axis2̲placement̲3d
SUBTYPE OF (placement);
axis : OPTIONAL direction;
ref̲direction : OPTIONAL direction;
DERIVE
p : LIST [3:3]OF direction := build̲axes(axis,ref̲direction);
WHERE
WR1: SELF\placement .location .dim = 3;
WR2: (NOT (EXISTS (axis))) OR (axis .dim = 3);
WR3: (NOT (EXISTS (ref̲direction))) OR (ref̲direction .dim = 3);
WR4: (NOT (EXISTS (axis))) OR (NOT (EXISTS (ref̲direction))) OR
(cross̲product(axis ,ref̲direction).magnitude > 0.0);
END̲ENTITY;
(*
属性定義
SELF\placement.location:参照点,すなわち,結合された配置座標系の原点の空間的な位置。
axis:局所座標系におけるZ軸の正確な方向を示すdirection。
ref̲direction:局所座標系におけるX軸の方向を定めるためのdirection。必要であれば,X軸の方向とaxis
との直交性を維持するために調整が行われる。axis及び/又はref̲directionが省略された場合,それらの
方向は,幾何座標系からとられる。
p:配置座標系の軸。これらの軸のdirectionは,必要に応じて,属性から適切な暗黙値を用いて得ること
ができる。
p[1]:局所座標系におけるX軸の方向を示す正規化されたdirection。
p[2]:局所座標系におけるY軸の方向を示す正規化されたdirection。
p[3]:局所座標系におけるZ軸の方向を示す正規化されたdirection。
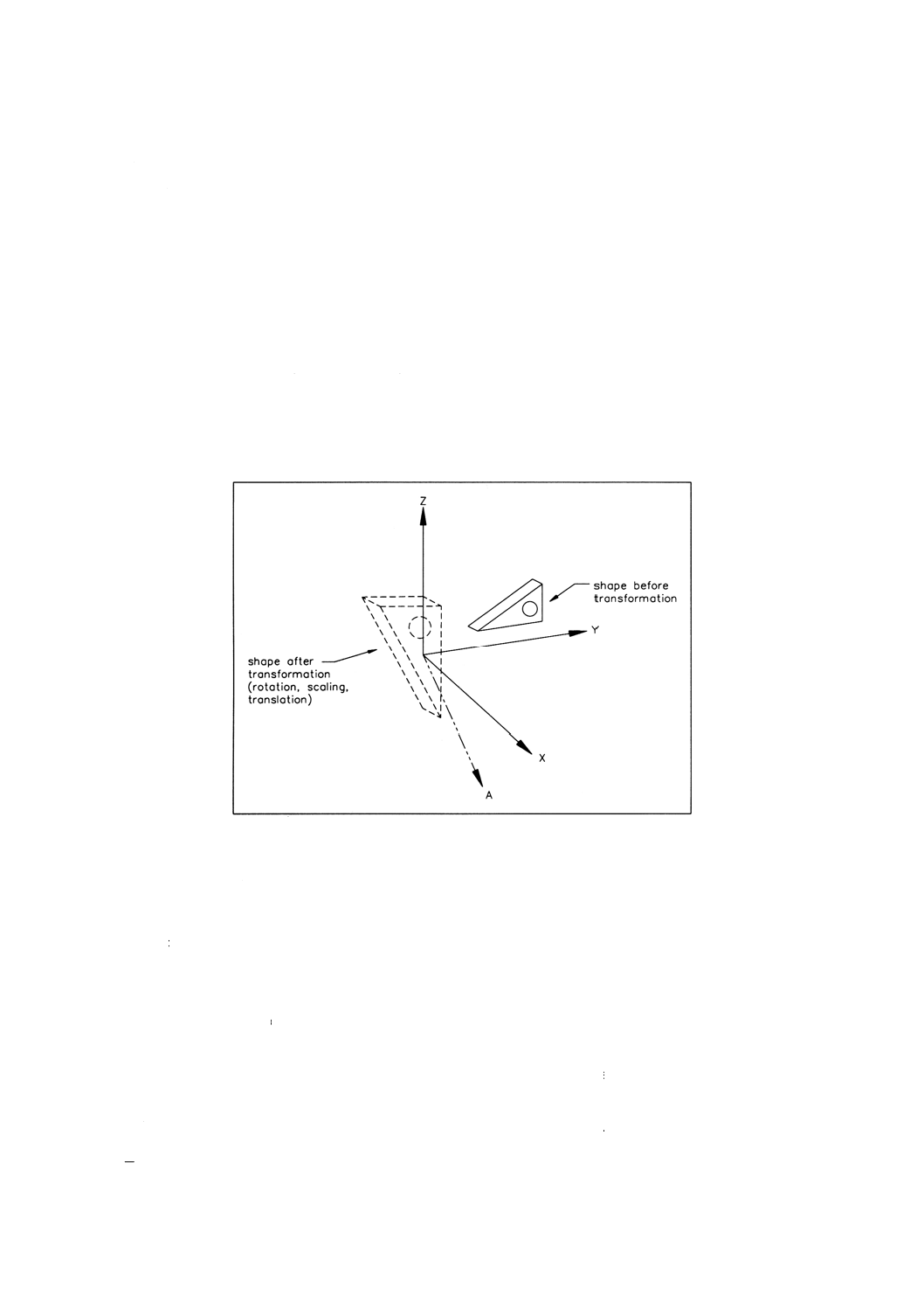
備考 属性の解釈については,図1参照。
形式的要件
WR1:SELF\placement.locationの空間次元数は,3とする。
WR2:axisの空間次元数は,3でなければならない。
WR3:ref̲directionの空間次元数は,3とする。
WR4:axis及びref̲directionは,平行又は逆向きに平行であってはならない(これはbuild̲axes関数に必
要である。)。
25
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.16 cartesian̲transformation̲operator cartesian̲transformation̲operatorは,平行移動,回転移動,鏡
像反転及び一様な拡大・縮小からなる幾何変換を定義する。
正規化されたベクトルのリストuは,直交行列Tの列を定義する。これらのベクトルは,関数base̲axis
によって,direction型の属性axis1及びaxis2から計算される。cartesian̲transformation̲operator̲3dの場合,
axis3も使われる。|T|=−1の場合,鏡像反転を含む。局所座標系の原点A,縮尺の倍率S,及び行列T,に
よって変換を定義する。
位置ベクトルがPであるpointに対する変換は,次のとおり定義される。
P→A+STP
方向がdであるdirectionに対する変換は,次のとおり定義される。
d→Td
図1 axis2̲placement̲3d
向きがdで,大きさがkであるvectorに対する変換は,次のとおり定義される。
d→Td
k→Sk
axis2̲placement型の属性をもつエンティティの場合には,配置座標系の方向を定義する誘導属性pは,先
に導出されてから変換が適用される。surfaceの場合には,変換後の任意の点での曲面の法線は,元の曲面
に対応する点における法線を変換することで得られる。長さの次元をもつ属性(円の半径など)を有する
幾何エンティティの場合には,その値はS倍される。
曲線上の曲面の場合には,pcurve.reference̲to̲curveは,いかなる変換にも影響されない。
cartesian̲transformation̲operatorは,各軸が同じ単位をもつ整合性のある単位系 (system of units) におい
て定義された幾何だけに適用されなければならない。すべての属性が省略された場合,変換は,恒等変換
とする。cartesian̲transformation̲operatorは,その下位型の一つとしてだけインスタンス化されなければな
らない。
26
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
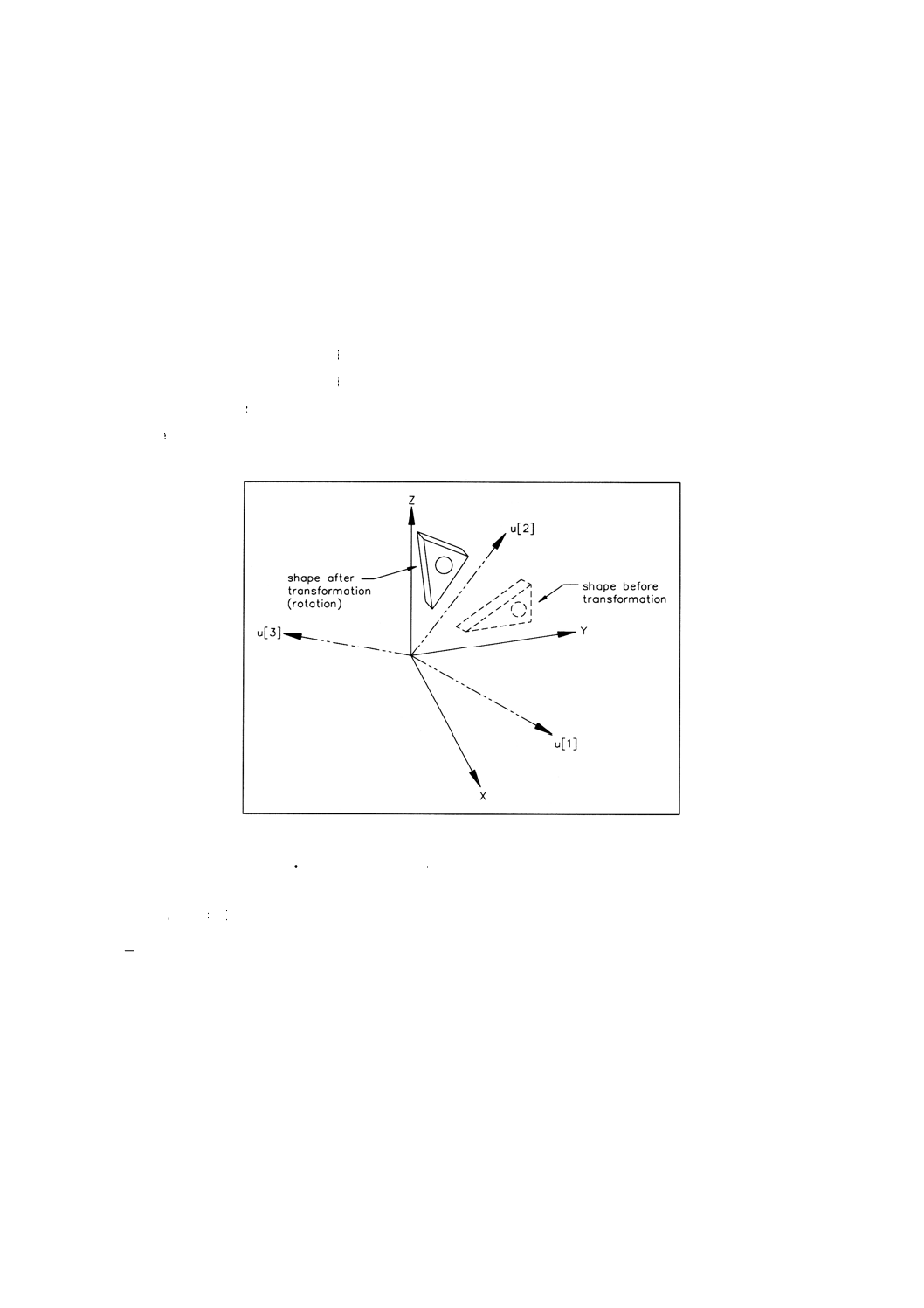
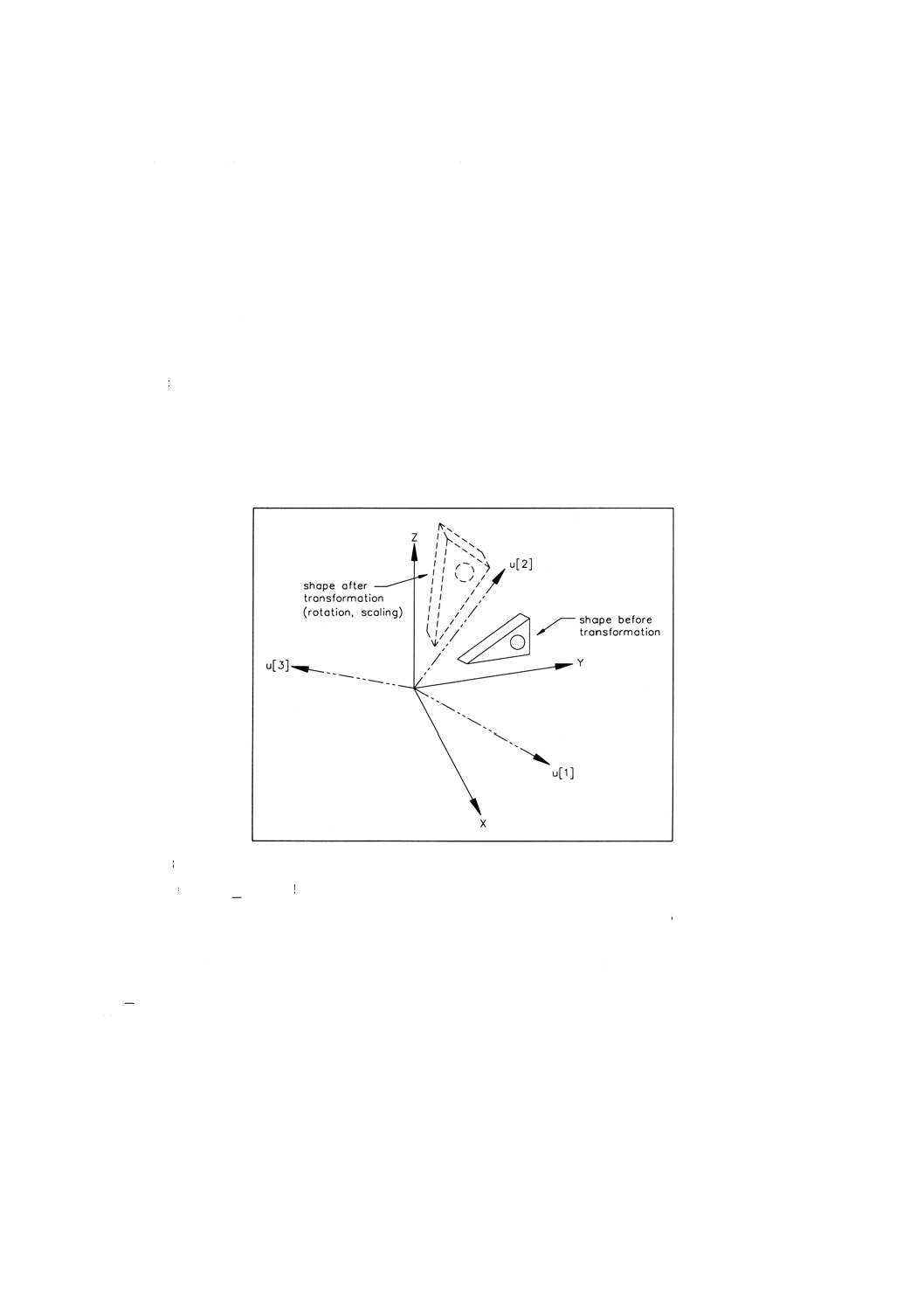
備考 変換の効果については,図2[(a)−(c)]参照。
EXPRESSによる定義
*)
ENTITY cartesian̲transformation̲operator
SUPERTYPE OF(ONEOF(cartesian̲transformation̲operator̲2d,
cartesian̲transformation̲operator̲3d))
SUBTYPE OF (geometric̲representation̲item,
functionally̲defined̲transformation);
axis1 : OPTIONAL direction;
axis2 : OPTIONAL direction;
local̲origin : cartesian̲point;
scale : OPTIONAL REAL;
図2 (a)cartesian̲transformation̲operator̲3d
DERIVE
sc1 : REAL := NVL(scale, 1.0);
WHERE
WR1: sc1 > 0.0;
END̲ENTITY;
(*
属性定義
axis1:導出されるX軸の方向を示すu[1]を定めるためのdirection。
axis2:導出されるY軸の方向を示すu[2]を定めるためのdirection。
local̲origin:平行移動を示すcartesian̲point。この属性は,省略できない変換における平行移動は,幾何空
間の原点からlocal̲originまでとする。
scale:変換のために指定された拡大・縮小の倍率。
scl:誘導属性の変換の倍率S。scaleが存在すればそれに等しく,存在しなければ1.0とする。
27
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
形式的要件
WR1:求められた縮尺sclは,0より大きくなければならない。
4.4.17 cartesian̲transformation̲operator̲3d cartesian̲transformation̲operator̲3dは,3次元空間内の平行
移動,回転移動,鏡像反転及び一様な拡大・縮小からなる幾何変換を定義する。
正規化されたベクトルのリストuは,直交行列Tの列を定義する。これらのベクトルは,関数base̲axis
によって,direction型の属性axis1,axis2及びaxis3から計算される。|T|=−1の場合,変換は,鏡像反転
を含む。
EXPRESSによる定義
*)
ENTITY cartesian̲transformation̲operator̲3d
SUBTYPE OF (cartesian̲transformation̲operator);
axis3 : OPTIONALdirection;
DERIVE
図2 (b)cartesian̲transformation̲operator̲3d
u : LIST[3:3]OF direction
:= base̲axis(3, SELF\cartesian̲transformation̲operator .axis1,
SELF\cartesian̲transformation̲operator .axis2,axis3);
WHERE
WR1: SELF\cartesian̲transformation̲operator .dim = 3;
END̲ENTITY;
(*
属性定義
SELF\cartesian̲transformation̲operator.axis1:導出されるX軸の方向を示すu[1]を定めるためのdirection。
必要であれば,u[1]は,u[3]と直交するように調整される。
SELF\cartesian̲transformation̲operator.axis2:導出されるY軸の方向を示すu[2]を定めるためのdirection。
必要であれば,u[2]は,u[1]及びu[3]と直交するように調整される。
28
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SELF\cartesian̲transformation̲operator.axis3:導出されるZ軸の方向を示すu[3]のdirection。
SELF\cartesian̲transformation̲operator.local̲origin:平行移動を示すcartesian̲point。この属性は,省略で
きない変換における平行移動は,幾何空間の原点からlocal̲originまでとする。
SELF\cartesian̲transformation̲operator.scale:変換のために指定された拡大・縮小の倍率。
SELF\geometric̲representation̲item.scl:誘導属性の変換の倍率S。scaleが存在すればそれに等しく,存在
しなければ1.0とする。
u:変換行列Tを定義する互いに直交する正規化されたベクトルのリスト。明示された属性axis3,axis1
及びaxis2からこの順で得られる。
形式的要件
WR1:このエンティティの座標空間の次元数は,3とする。
4.4.18 cartesian̲transformation̲operator̲2d cartesian̲transformation̲operator̲2dは,2次元空間内の平行
移動,回転移動,鏡像反転及び一様な拡大・縮小からなる幾何変換を定義する。
図2 (c)cartesian̲transformation̲operator
正規化されたベクトルのリストuは,直交行列Tの列を定義する。これらのベクトルは,関数base̲axis
によってdirection型の属性axis1及びaxis2から計算される。|T|=−1の場合,変換は,鏡像反転を含む。
EXPRESSによる定義
*)
ENTITY cartesian̲transformation̲operator̲2d
SUBTYPE OF (cartesian̲transformation̲operator);
DERIVE
u : LIST[2:2]OF direction :=
base̲axis(2,SELF\cartesian̲transformation̲operator .axis1,
SELF\cartesian̲transformation̲operator .axis2,?);
WHERE
WR1: SELF\cartesian̲transformation̲operator .dim = 2;
END̲ENTITY;
29
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(*
属性定義
SELF\cartesian̲transformation̲operator.axis1:導出されるX軸の方向を示すu[1]を定めるためのdirection。
SELF\cartesian̲transformation̲operator.axis2:導出されるY軸の方向を示すu[2]を定めるためのdirection。
SELF\cartesian̲transformation̲operator.local̲origin:平行移動を示すcartesian̲point。この属性は,省略で
きない変換における平行移動は,幾何空間の原点からlocal̲originまでとする。
SELF\cartesian̲transformation̲operator.scale:変換のために指定された拡大・縮小の倍率。
SELF\cartesian̲transformation̲operator.scl:誘導属性の変換の倍率S。scaleが存在すればそれに等しく,存
在しなければ1.0とする。
u:変換行列Tを定義する互いに直交する正規化されたベクトルのリスト。明示された属性axis1及びaxis2
からこの順で得られる。
形式的要件
WR1:このエンティティの座標空間の次元数は,2とする。
4.4.19 curve curve(曲線)は,座標空間の中を動く点の軌跡とみなす。
EXPRESSによる定義
*)
ENTITY curve
SUPERTYPE OF (ONEOF(line, conic, pcurve, surface̲curve,
offset̲curve̲2d, offset̲curve̲3d, curve̲replica))
SUBTYPE OF (geometric̲representation̲item);
END̲ENTITY;
(*
非形式的要件
IP1:curveは,弧状連結とする。
IP2:curveは,0を超える弧長をもたなければならない。
4.4.20 line line(直線)は,一定の接線方向をもった境界のないcurveとする。lineは,point及びdirection
によって定義する。lineの正の方向はvector型dirの方向とする。
曲線は,次のとおりパラメタ化される。
P=pnt
V=dir
λ(u)=P+uV
パラメタ範囲は,−∞<u<∞とする。
EXPRESSによる定義
*)
ENTITY line
SUBTYPE OF (curve);
pnt : cartesian̲point;
dir : vector;
WHERE
WR1: dir.dim = pnt.dim;
30
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲ENTITY;
(*
属性定義
pnt:lineの配置。
dir:lineの方向。dirの大きさ及び単位は,lineのパラメタ化に影響する。
SELF\geometric̲representation̲item.dim:lineに対する座標空間の次元数。これは,上位型
geometric̲representation̲itemから継承された属性とする。
形式的要件
WR1:pnt及びdirは,両者ともに,2次元のエンティティ又は3次元のエンティティとする。
4.4.21 conic conic(円錐曲線)は,平面と円錐との交差によって生成できる平面曲線とする。
conicは,他の幾何によってではなく,自身の幾何的な性質によって定義する。
conicは,常に,axis2̲placementによって定義された配置座標系をもつ。パラメタ表現は,この配置座標
系によって定義する。
EXPRESSによる定義
*)
ENTITY conic
SUPERTYPE OF (ONEOF(circle, ellipse, hyperbola, parabola))
SUBTYPE OF (curve);
position: axis2̲placement;
END̲ENTITY;
(*
属性定義
position:conicの配置及び向き。この属性に関する解釈の詳細は,個別の下位型に対して与えられる。
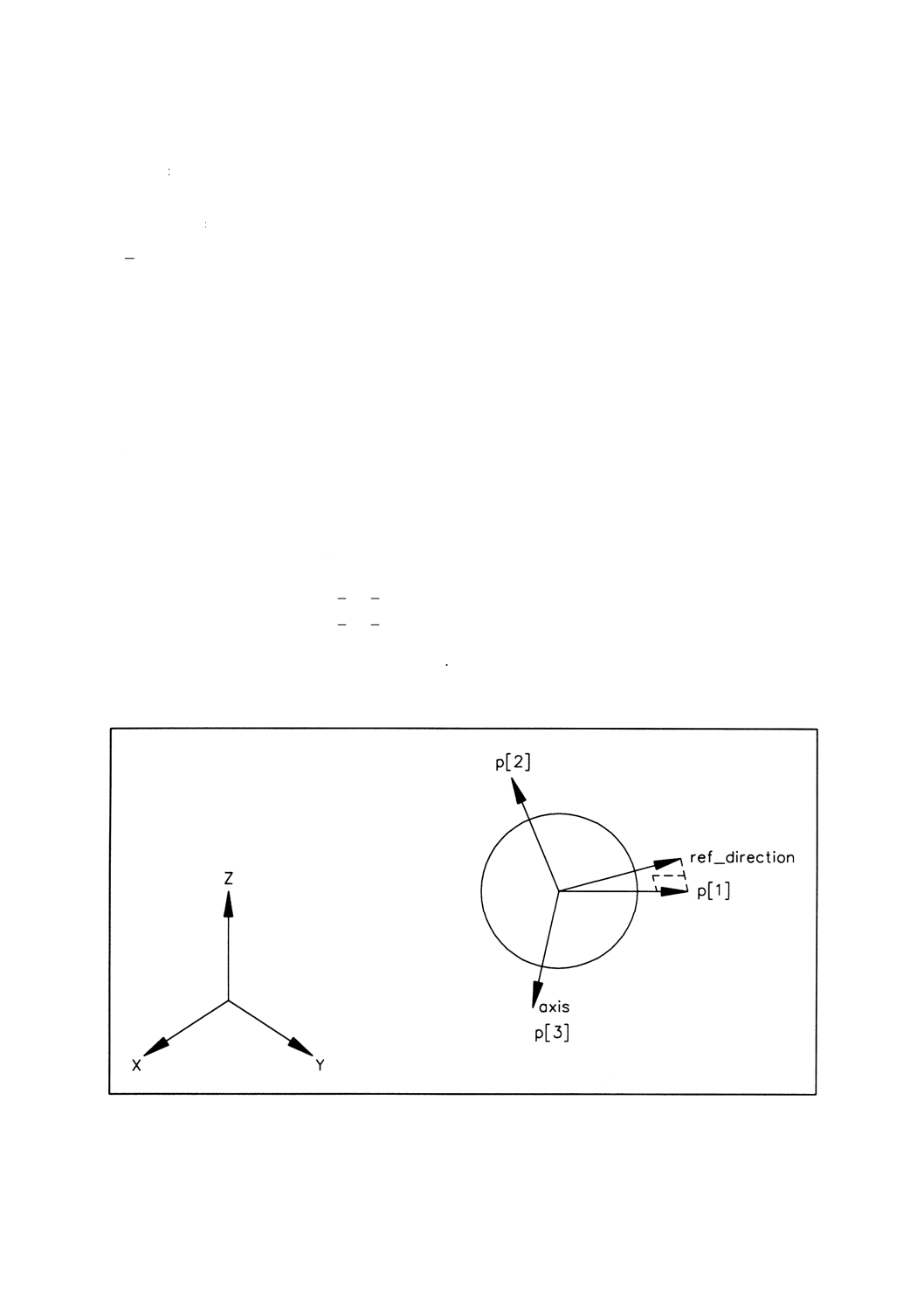
4.4.22 circle circle(円)は,半径並びに円の配置及び向きによって定義する。データは,次のとおり解
釈する。
C=position.location(中心)
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=radius
更にcircleは,次のとおりパラメタ化する。
λ(u)=C+R((cos u)x+(sin u)y)
パラメタ化範囲は,0°≦u≦360°とする。
上で定義された配置座標系において,circleは,方程式C=0を満たす。ここで,
C(x, y, z)=x2+y2-R2
とする。任意の点におけるcircleの正の向きは,次式で与えられる曲線の接線方向Tとする。
T=(-Cy, Cx,0)
備考 円弧は,エンティティtrimmed̲curveをエンティティcircleとともに使用することによって
定義する。
EXPRESSによる定義
31
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
ENTITY circle
SUBTYPE OF (conic);
radius : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\conic.position.location:この継承された属性は,円の中心を定義する。
radius:円の半径。これは,0より大きくなければならない。
備考 属性の解釈は,図3による。
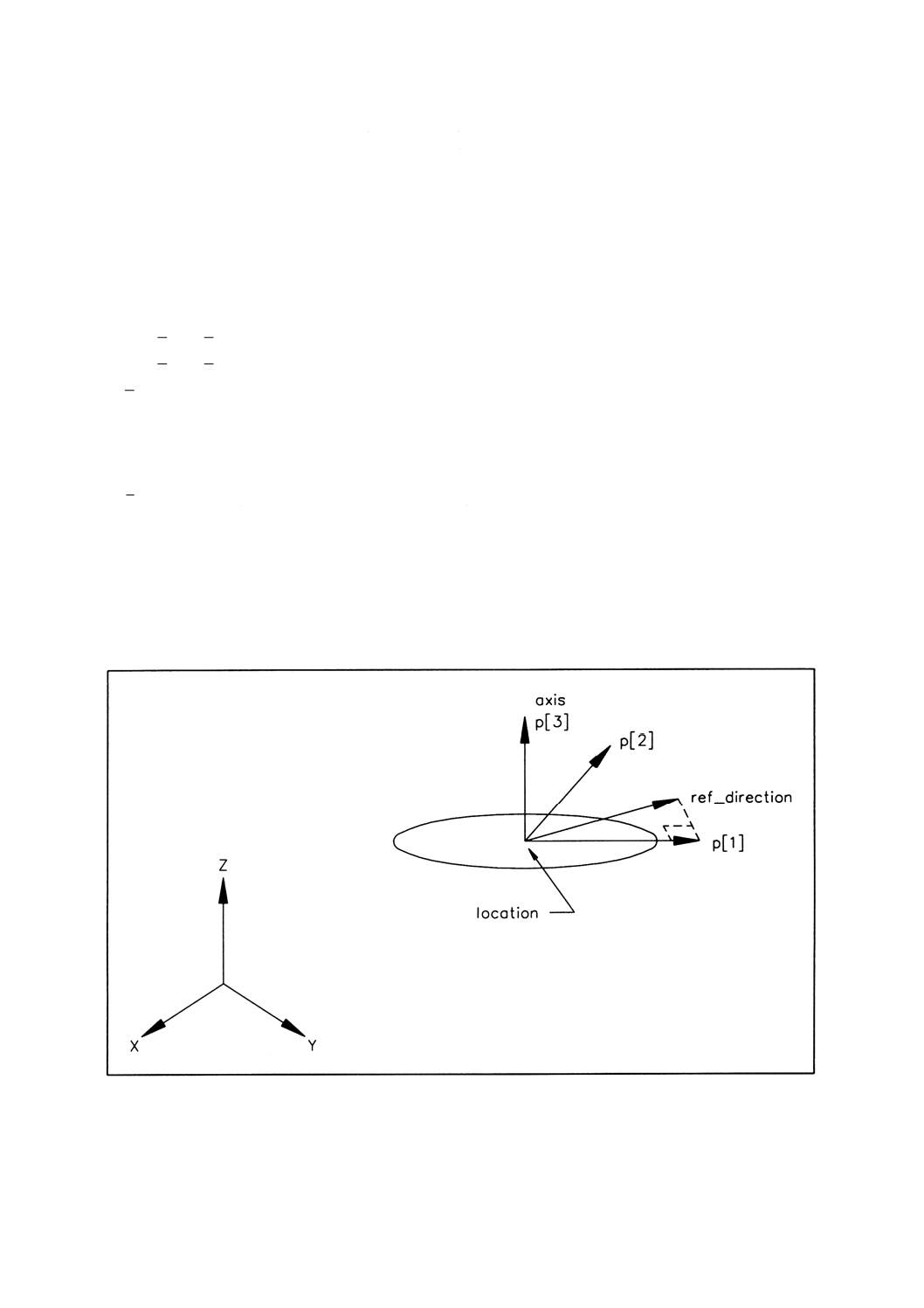
4.4.23 ellipse ellipse(だ円)は,長半径及び短半径の長さ,並びに曲線の位置(中心,すなわち,焦点
を結ぶ線分の中点)及び向きによって定義される円錐曲線とする。
データは,次のとおり解釈する。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
R1=semi̲axis̲1
R2=semi̲axis̲2
更にellipseは,次のとおりパラメタ化する。
λ(u)=C+(R1 cos u)x+(R2 sin u)y
図3 circle
パラメタ化範囲は,0°≦u≦360°とする。
上で定義された配置座標系において,ellipseは,方程式C=0を満たす。ここで,
32
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
/
/
)
,
,
(
22
2
21
2
−
+
=
R
y
R
x
z
y
x
C
とする。任意の点におけるellipseの正の向きは,次式で与えられる曲線の接線方向Tとする。
T=(-Cy, Cx, 0)
EXPRFSSによる定義
*)
ENTITY ellipse
SUBTYPE OF (conic);
semi̲axis̲1 : positive̲length̲measure;
semi̲axis̲2 : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\conic.position:SELF\conic.position.locationは,だ円の中心とし,SELF\conic.position.p[1]は,
semi̲axis1に対応する軸の方向とする。
semi̲axis̲1:だ円の第1の半径とする。正でなければならない。
semi̲axis̲2:だ円の第2の半径とする。正でなければならない。
備考 属性の解釈は,図4による。
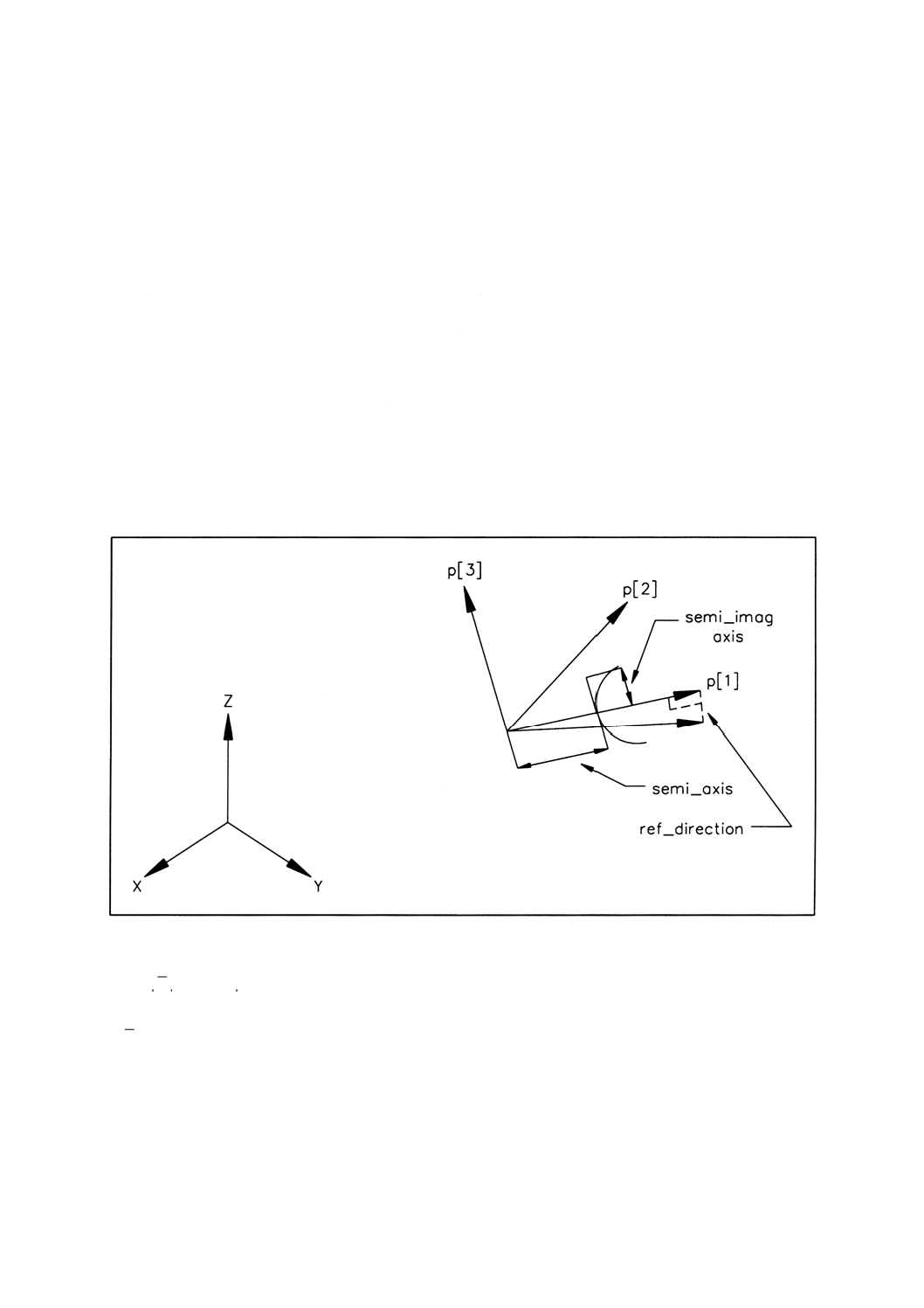
4.4.24 hyperbola hyperbola(双曲線)は,長半径(major radius)及び短半径(minor radius)の長さ,並
びに曲線の位置(焦点を結ぶ線分の中点)及び向きによって定義される円錐曲線とする。
図4 ellipse
データは,次のとおり解釈する。
C=position.location
x=position.p[1]
y=position.p[2]
33
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
z=position.p[3]
R1=semi̲axis
R2=semi̲imag̲axis
更にhyperbolaは,次のとおりパラメタ化する。
λ(u)=C+(R1 cosh u)x+(R2 sinh u)y
パラメタ化範囲は,-∞<u<∞とする。
上で定義された配置座標系において,hyperbolaは,方程式C=0を満たす。ここで,
1
/
/
)
,
,
(
22
2
21
2
−
−
=
R
y
R
x
z
y
x
C
とする。任意の点におけるhyperbolaの正の向きは,次式で与えられる曲線の接線方向Tとする。
T=(−Cy, Cx, 0)
表現されているhyperbolaは,x方向に存在するものだけとする。
EXPRESSによる定義
*)
ENTITY hyperbola
図5 hyperbola
SUBTYPE OF (conic);
semi̲axis : positive̲length̲measure;
semi̲imag̲axis : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\conic.position:曲線の配置及び向き。SELF\conic.position.locationは,hyperbolaの中心とし,SELF
\conic.position.p[1]は,semi̲axisに対応する方向とする。定義される曲線は,SELF\conic.position.p[1]の
正の側に存在する。
34
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
semi̲axis:hyperbolaの半軸 (semi axis) の長さ。これは,正とし,hyperbolaの2本の曲線の間の最短距離
の半分とする。
semi̲imag̲axis:hyperbolaの半虚軸 (semi imagenary axis) の長さ。正でなければならない。
備考 属性の解釈は,図5による。
形式的要件
WR1:semi̲axisの長さは,0より大きくなければならない。
WR2:semi̲imag̲axisの長さは,0より大きくなければならない。
4.4.25 parabola parabola(放物線)は,その焦点距離,位置(頂点)及び向きによって定義される円錐
曲線とする。
データは,次のとおり解釈する。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
F=focal̲dist
図6 parabola
更にparabolaは,次のとおりパラメタ化する。
λ(u)=C+F(u2x+2uy)
パラメタ化範囲は,−∞<u<∞とする。
上で定義された配置座標系において,放物線は,方程式C=0を満たす。ここで,
C(x, y, z)=4Fx−y2
とする。任意の点における曲線の正の向きは,次式で与えられる曲線の接線方向Tとする。ここで,
T=(-Cy, Cx, 0)
とする。
EXPRESSによる定義
35
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
ENTITY parabola
SUBTYPE OF (conic);
focal̲dist : length̲measure;
WHERE
WR1: foca1̲dist <> 0.0;
END̲ENTITY;
(*
属性定義
SELF\conic.position:曲線の配置及び向き。SELF\conic.position.locationは,放物線の頂点とし,SELF\
conic.position.p[1]は,対称軸とする。
focal̲dist:頂点から焦点までの距離。
備考 属性の解釈は,図6による。
形式的要件
WR1:焦点距離は,0であってはならない。
4.4.26 bounded̲curve bounded̲curveは,同定可能な端点をもつ有限弧長のcurveとする。
EXPRESSによる定義
*)
ENTITY bounded̲curve
SUPERTYPE OF (ONEOF(polyline, b-spline̲curve, trimmed̲curve,
bounded̲pcurve, bounded̲surface̲curve, composite̲curve))
SUBTYPE OF (curve);
END̲ENTITY;
(*
非形式的要件
IP1:bounded̲curveは,有限弧長をもつ。
IP2:bounded̲curveは,開始点及び終了点をもつ。
4.4.27 polyline polylineは,n個の点P1〜Pnのリストによって定義されるn−1個の直線セグメントから
なるbounded̲curveとする。
曲線のi番目のセグメントは,次のとおりパラメタ化する。
λ(u)=Pi(i-u)+Pi+1(u+1−i) ただし,1≦i≦n−1
ここで、i−1≦u≦iとし,かつパラメタ範囲は0≦u≦n−1とする。
EXPRESSによる定義
*)
ENTITY polyline
SUBTYPE OF (bounded̲curve);
points : LIST[2:?]OF cartesian̲point;
END̲ENTITY;
(*
属性定義
36
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
points:polylineを定義するpoint。
4.4.28 b̲spline̲curve b̲spline̲curve(B-スプライン曲線)は,制御点及び基底関数によって定義される
区分的な多項式又は有理式のパラメタ曲線とする。b̲spline̲curveは,多項式又は有理式のパラメタ的な曲
線のすべての型を表現するための最も安定した形式として選択された。適切な属性の値によって,明示的
な多項式,有理式,ベジエ又はB-スプラインの各型の単一のセグメント又はスプライン曲線を表現するこ
とができる。b̲spline̲curveは,単純な暗黙の設定が可能なように,ノット及びノット多重度が導出できる
特別な下位型を3個もつ。
備考1. b̲spline̲curveの暗黙値及び下位型の識別は,性能の考慮のために及び計算の実行におけ
る効率の問題のために重要である。
2. B-スプラインが有理式であるとは,重みの中に等しくないものが存在することをいう。
これは,下位型rational̲b̲spline̲curveによって表現することができる。多項式ならば,
重みは,すべて暗黙で1にしてもよい。
3. b̲spline̲curveが一様,準一様,又はベジエの場合(区分的ベジエの場合を含む。),ノッ
ト及びノット多重度は,暗黙にしてもよい(すなわち,属性定義によって指定されたデ
ータが存在しなくてもよい。)。
4. ノットを暗黙にする場合,離れたノットの間の差は,1.0が仮定され,その曲線の有効な
パラメタ範囲は,0.0から始まる。これらの暗黙は,下位型が与える。
5. 非一様の場合には,ノット及びノット多重度は,暗黙にしてはならない。
6. 重み及びノットの暗黙化は,互いに独立に行われる。
7. B-スプライン基底関数
)
(u
Ndi
の定義は,附属書E(参考)のE1〜E3による。これらの参
考文献における用語の違いには,注意を要する。
データは,次のとおりに解釈する。
(a) 多項式の場合,曲線は,次で与えられる。
∑
k
i
di
i
u
N
u
0
)
(
)
(
=
=
P
λ
(b) 有理式の場合,すべての重みは,正でなければならない。更に曲線は,次で与えられる。
∑∑ki
di
i
k
i
di
i
i
u
N
w
u
N
w
u
0
0
)
(
)
(
)
(
=
=
=
P
λ
ここで,
k+1= 制御点の数
Pi= 制御点
wi= 重み
d= 次数
とする。ノット配列は,(d+k+2) 個の実数 [u-d, …, uk+1] の配列であって,すべての添字j∈[−d, k] に対し
てuj≦uj+1が成り立つものとする。この配列は,リストknotsから,多重度に応じて各多重ノットを繰り返
すことで得られる。i番目の次数dの正規化されたB-スプライン基底関数
di
Nは,この配列の部分集合 [ui
−d, …, ui+1] 上で定義される。
(c) Lをノットリストのd+k+2個のノットの中の相異なる値の個数とする。Lは,“ノットの添字の上限
37
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(upper̲index̲of̲knots)”として参照される。mjを,相異なるノットのj番目の値の多重度(すなわち反
復の数)とする。したがって
2
0
+
+
=
=
k
d
m
L
i
i
∑
となる。すべてのノット多重度は,最初のもの及び最後のものを除き,1〜dの範囲になければならない。
最初のもの及び最後のものは,最大でd+1をとることができる。基底関数の値を求める場合,例えば,多
重度3のノットuは,ノット配列における並びu,u,uとして解釈される。
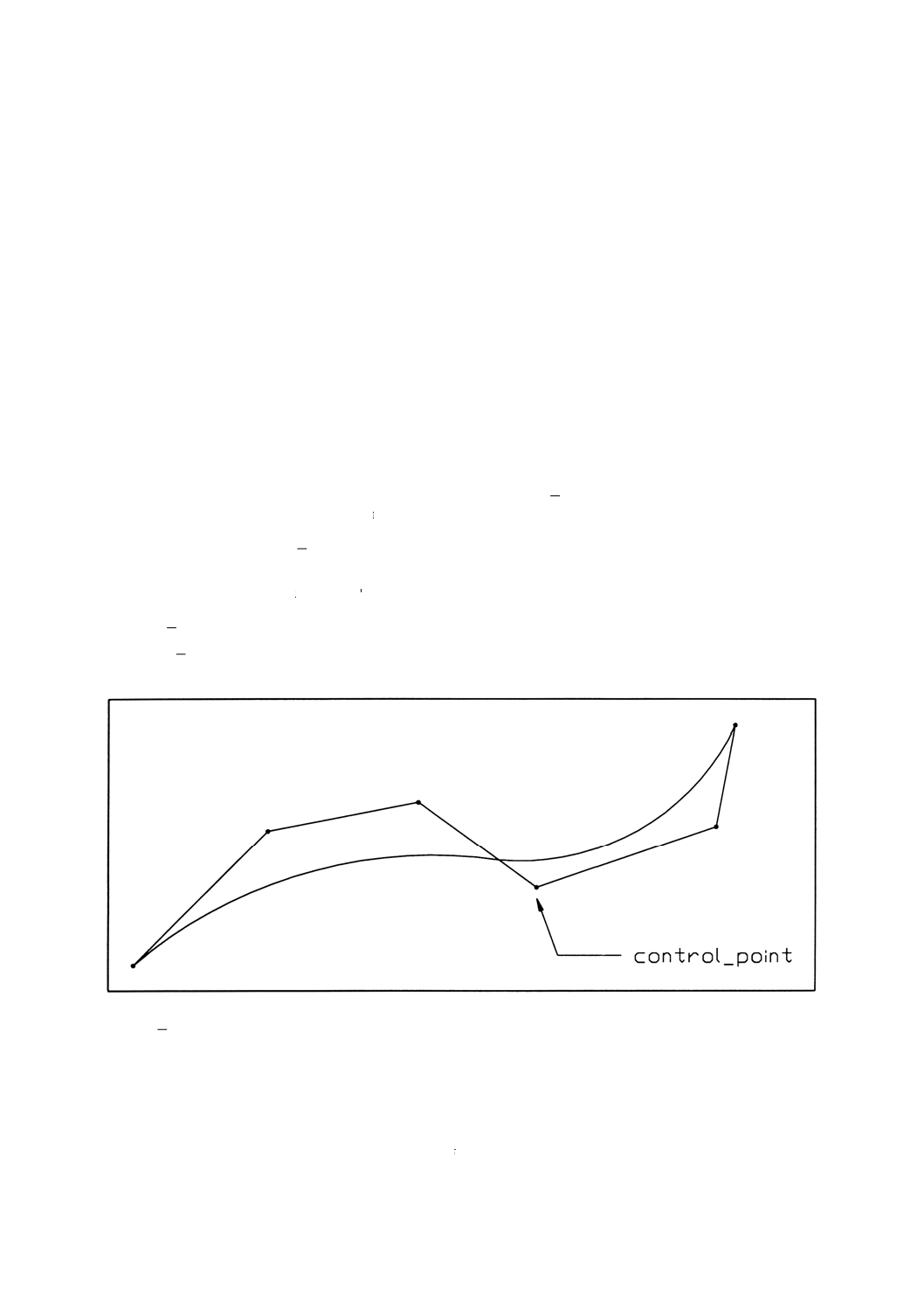
備考 曲線定義の制御点に関する詳細な情報は,図7による。
EXPRESSによる定義
*)
ENTITY b̲spline̲curve
SUPERTYPE OF (ONEOF(uniform̲curve, b̲spline̲curve̲with̲knots,
quasi̲uniform̲curve, bezier̲curve)
ANDOR rational̲b̲spline̲curve)
SUBTYPE OF (bounded̲curve);
degree : INTEGER;
control̲points̲list : LIST [2:?]OF cartesian̲point;
curve̲form : b̲spline̲curve̲form;
closed̲curve : LOGICAL;
図7 b̲spline̲curve
self̲intersect : LOGICAL;
DERIVE
upper̲index̲on̲control̲points
:INTEGER
:= (SIZEOF(control̲points̲list) -1);
control̲points
: ARRAY [0:upper̲index̲on̲control̲points]
OF cartesian̲point
38
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
:= list̲to̲array(control̲points̲list,0,
upper̲index̲on̲control̲points);
WHERE
WR1:('GEOMETRY-SCHEMA.UNIFORM̲CURVE' IN TYPEOF(self)) OR
('GEOMETRY̲SCHEMA.QUASI̲UNIFORM̲CURVE' IN TYPEOF(self)) OR
('GEOMETRY-SCHEMA.BEZIER̲CURVE' IN TYPEOF(self)) OR
('GEOMETRY̲SCHEMA.B̲SPLINE̲CURVE̲WITH̲KNOTS' IN TYPEOF(self));
END̲ENTITY;
(*
属性定義
degree:基底関数の代数的な次数。
control̲points̲list:曲線の制御点のリスト。
curve̲form:特定の曲線形状の識別子。これは,参考とする(詳細は,4.3.4参照)。
closed̲curve:曲線が閉じているかどうかの表示。これは,参考とする。
self̲intersect:曲線が自己干渉するかどうかを示すフラグ。これは,参考とする。
SELF\geometric̲representation̲item.dim:曲線の座標空間の次元数。
upper̲index̲on̲control̲points:制御点の配列の添字の上限。添字の下限は,0とする。この値は,control̲points
から導出される。
control̲points:曲線の幾何を定義するために使われる制御点の配列。これは,control̲points̲listから導出
される。
備考 データの一部が“参考”として記述されている属性値と曲線自身から得られる特性とが一
致しない場合,曲線データが優先される。
形式的要件
WR1:このエンティティのインスタンス化は,下位型のb̲spline̲curve̲with̲knots, uniform̲curve,
quasi̲uniform̲curve又はbezier̲curveのうちの1個でなければならない。
4.4.29 b̲spline̲curve̲with̲knots これは,b̲spline̲curveの下位型であって,ノットの値が明示的に与え
られるものとする。この下位型は,非一様なb̲spline̲curveを表現するために用いるが,他のknot̲typeの
ために用いてもよい。
Lをノットリストのd+k+2個のノットの中の相異なる値の個数とする。Lは,“ノットに対する添字の
上限 (upper̲index̲on̲knots) ”として参照される。mjを,相異なるノットのj番目の値の多重度(すなわ
ち,反復の数)とする。
したがって
2
1
+
+
=
=
k
d
m
L
i
i
∑
となる。
すべてのノット多重度は,最初のもの及び最後のものを除き,1〜dの範囲になければならない。最初の
もの及び最後のものは,最大でd+1をとることができる。
基底関数の値を求める場合,例えば,多重度3のノットuは,ノット配列における並びu, u, uとして解
釈される。
39
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
ENTITY b̲spline̲curve̲with̲knots
SUBTYPE OF (b̲spline̲curve);
knot̲multiplicities : LIST [2:?]OF INTEGER;
knots : LIST [2:?]OF parameter̲value;
knot̲spec : knot̲type;
DERIVE
upper̲index̲on̲knots : INTEGER := SIZEOF(knots);
WHERE
WR1: constraints̲param̲b̲spline(degree, upper̲index̲on̲knots,
upper̲index̲on̲control̲points,
knot̲multiplicities, knots);
WR2: SIZEOF(knot̲multiplicities) = upper̲index̲on̲knots;
END̲ENTITY;
(*
属性定義
knot̲multiplicities:ノットの多重度。このリストは,ノットの配列を構築する際にリストknots中の各ノッ
トが繰り返される回数を定義する。
knots:B-スプライン基底関数を定義するために使用される相異なるノットのリスト。
knot̲spec:ノットの種類の記述。これは,参考とする。
SELF\b̲spline̲curve.curve̲form:特定の曲線形状の識別子。これは,参考とする(詳細は,4.3.4参照)。
SELF\b̲spline̲curve.degree:基底関数の代数的な次数。
SELF\b̲spline̲curve.closed̲curve:曲線が閉であるかどうかの表示。これは,参考とする。
SELF\b̲spline̲curve.self̲intersect:曲線が自己干渉するかどうかを示すフラグ。これは,参考とする。
dim:曲線の座標空間の次元数。
SELF\b̲spline̲curve.upper̲index̲on̲control̲points:制御点の配列の添字の上限。添字の下限は,0とする。
この値は,control̲points̲listから導出される。
upper̲index̲on̲knots:ノットの配列の添字の上限。添字の下限は,1とする。
SELF\b̲spline̲curve.control̲points:曲線の幾何を定義するために使われる制御点の配列。これは,
control̲points̲listから導出される。
備考 データの一部が“参考”として記述されている属性値と曲線自身から得られる特性とが一
致しない場合,曲線データが優先される。
形式的要件
WR1:B-スプラインのパラメタ化において矛盾が見いだせない場合,constraints̲param̲b̲splineは,TRUE
を返す。
WR2:ノット多重度のリスト中の要素の個数は,ノットのリスト中の要素の個数と等しくなければならな
い。
4.4.30 uniform̲curve これは,b̲spline̲curveの特殊な下位型とし,ノットが等間隔に配置されたものと
する。この場合,ノット及びノット多重度に対して,適切な暗黙値が導出される。
40
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B-スプラインが一様であるとは,すべてのノット多重度が1で、すべてのノットが直前のノットとある
正の定数だけ異なることをいう。この下位型では,ノットは,−dから始まり,間隔は1.0とする。ここで,
dは次数とする。
備考 b̲spline̲curveが,一様でかつdegree=1の場合,polylineと等価とする。
EXPRESSによる定義
*)
ENTITY uniform curve
SUBTYPE OF (b̲spline̲curve);
END̲ENTITY;
(*
備考 値k̲upは,ノット及びノット多重度のリストの添字の上限に必要なことがある。これは,
次数及び制御点の個数から計算される。
k̲up=SELF\b̲spline̲curve.upper̲index̲on̲control̲points+degree+2
必要ならば,ノット及びノット多重度は,次の関数呼び出しによって計算することがで
きる。
default̲b̲spline̲knots(SELF\b̲spline̲curve.degree, k̲up, uniform̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲curve.degree, k̲up, uniform̲knots)
4.4.31 quasi̲uniform̲curve これは,b̲spline̲curveの特殊な下位型とし,最初のもの及び最後のものを
除き,ノットは,等間隔に配置され,多重度1をもつ。この場合,ノット及びノット多重度に対して,適
切な暗黙値が導出される。
B-スプラインが準一様であるとは,ノットが端点では多重度 (degree+1) を,それ以外では多重度1をも
ち,各ノットが直前のノットから,ある正の定数だけ異なることをいう。2個のノットだけをもつ
quasi̲uniform̲curveは,ベジエ曲線を表現する。この下位型では,ノットは,0.0から始まり,その間隔は
1.0とする。
EXPRESSによる定義
*)
ENTITY quasi̲uniform̲curve
SUBTYPE OF (b̲spline̲curve);
END̲ENTITY;
(*
備考 値k̲upは,ノット及びノット多重度のリストの添字の上限に必要なことがある。これは,
次数及び制御点の個数から計算される。
k̲up=SELF\b̲spline̲curve.upper̲index̲on̲control̲points̲degree+2
必要ならば,ノット及びノット多重度は,次の関数呼び出しによって計算することがで
きる。
default̲b̲spline̲knots(SELF\b̲spline̲curve.degree, k̲up, quasi̲uniform̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲curve.degree, k̲up, quasi̲uniform̲knots)
4.4.32 bezier̲curve この下位型は,最も一般的な場合,区分的ベジエ曲線を表す。これは,b̲spline̲surface
の特殊な下位型とし,ノットが等間隔で,高い多重度をもつものとする。この場合,ノット及びノット多
重度に対して,適切な暗黙値が導出される。
41
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b̲spline̲curveは,内部ノットの多重度が1ではなくdegreeであることを除いて準一様ならば,区分的
ベジエ曲線とする。この下位型では,ノットは0.0から始まり,その間隔は1.0とする。2個のノット0.0
及び1.0だけをもち,それぞれの多重度が(次数+1)の区分的ベジエ曲線は,単純なベジエ曲線とする。
備考1. 単純なベジエ曲線は,次のデータによって,ノットをもったb̲spline̲curveとして定義
できる。
次数
(d)
制御点の添字の上限
(dに等しい)
制御点
(d+1個のcartesian̲point)
ノット列の種類
(準一様ノットに等しい)
ノット多重度
(d+1,d+1)
ノット
(0.0,1.0)
有理ベジエ曲線を除いて,これ以外のデータは不要とする。有理ベジエ曲線の場合,
重みのデータ[ (d+1) 個の実数]が与えられなければならない。
2. 区分的ベジエ曲線は,b̲spline̲curveとしての等価な表現をもつ。非一様なノットの問題
のため,b̲spline̲curveの中には,区分的ベジエ曲線として表現できないものも存在する。
区分的ベジエ曲線をB-スプラインとして定義するためには,次のとおりとする。
− 最初のノットは0.0とし,多重度は(d+1)とする。
− 次のノットは1.0とし,それか最後でなければ,多重度はdとする(1番目のセグメ
ントに対するノットの定義。)。
− その次のノットは2.0とし,それが最後でなければ,多重度は,dとする(2個のセ
グメントに対するノットの定義。)。
− これを最後のセグメントの終点まで続ける。最後のセグメントがn番目のとき,そ
の終点のノットをnとし,多重度は(d+1)とする。
例6. 1個のセグメントからなる3次のベジエ曲線は,多重度列(4,4)のノット列(0,1)
をもつことになる。
例7. 2個のセグメントからなる3次の区分的ベジエ曲線は,多重度列(4,3,4)のノッ
ト列(0,1,2)をもつことになる。
3. 区分的ベジエの場合は,dを次数,k+1を制御点の個数,mを多重度dのノットの個数,
及びNをスプラインのノットの総数とすると,次のとおりになる。
(d+2+k)=N
=(d+1)+md+(d+1)
したがって,
m=(k−d)/d
である。ノット列は (0,1,…,m,(m+1)) で,多重度列 (d+1,d,…,d,d+1) をもつ。
EXPRESSによる定義
*)
ENTITY bezier curve
SUBTYPE OF (b̲spline̲curve);
END̲ENTITY;
(*
42
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 値k̲upは,ノット及びノット多重度のリストの添字の上限に必要なことがある。これは,
次数及び制御点の個数から計算される。
1
.
̲
̲
int
̲
̲
̲
̲
.
̲
̲
̲
+
\
\
=
degerr
curve
spline
b
SELF
s
po
control
on
index
upper
curve
spline
b
SELF
up
k
必要ならば,ノット及びノット多重度は,次の関数呼び出しによって計算することがで
きる。
default̲b̲spline̲knots(SELF\b̲spline̲curve.degree, k̲up, piecewise̲bezier̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲curve.degree, k̲up, piecewise̲bezier̲knots)
4.4.33 rational̲b̲spline̲curve rational̲b̲spline̲curveは,制御点及び基底関数によって記述された区分
的パラメタ有理曲線とする。この下位型は,b̲spline̲curveの他の下位型の一つ(これは,基底関数を定義
するためのノットの値を,明示的に又は暗黙に与える。)とともにインスタンス化される。
重みは,すべて正でなければならない。更に,曲線は,次で与えられる。
∑∑ki
di
i
k
i
di
i
i
u
N
w
u
N
w
u
0
0
)
(
)
(
)
(
=
=
=
P
λ
ここで,
k+1= 制御点の個数
Pi= 制御点
wi= 重み
d= 次数
とする。
EXPRESSによる定義
*)
ENTITY rational̲b̲spline̲curve
SUBTYPE OF (b̲spline̲curve);
weights̲data : LIST [2:?]OF REAL;
DERIVE
weights : ARRAY [0:upper̲index̲on̲control̲points]OF REAL
:= list̲to̲array(weights̲data,0,
upper̲index̲on̲control̲points);
WHERE
WR1: SIZEOF(weights̲data) = SIZEOF(SELF\b̲spline̲curve.control̲points̲list);
WR2: curve̲weights̲positive(SELF);
END̲ENTITY;
(*
属性定義
weights̲data:与えられた重み。誘導属性のweightsを参照。
SELF\b̲spline̲curve.degree:基底関数の代数的次数。
SELF\b̲spline̲curve.curve̲form:特定の曲線形状の識別子。これは,参考とする(詳細は,4.3.4参照)。
43
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SELF\b̲spline̲curve.closed̲curve:曲線が閉じているかどうかの表示。これは,参考とする。
SELF\b̲spline̲curve.self̲intersect:曲線が自己干渉するかどうかを示すフラグ。これは,参考とする。
SELF\b̲spline̲curve.upper̲index̲on̲control̲points:制御点の配列の添字の上限。添字の下限は,0とする。
この値は,control̲points̲listから導出される。
SELF\b̲spline̲curve.control̲points:曲線の幾何を定義するために使われる制御点の配列。これは,
control̲points̲listから導出される。
weights:制御点に関連付けられた重みの配列。これは,weights̲dataから導出される。
備考 データの一部が“参考”として記述されている属性値と曲線自身から得られる特性とが一
致しない場合,曲線データが優先される。
形式的要件
WR1:重みの個数と制御点の個数とは,同じでなければならない。
WR2:すべての重みは,0.0を超えなければならない。
4.4.34 trimmed̲curve trimmed̲curveは,関連付けられたbasis̲curveから,2個の識別された点の間を選
択することによって生成されるbounded̲curveとする。basis̲curve自体は不変であって,2個以上の
trimmed̲curveが同じ基底曲線を参照してもよい。曲線に対するトリム点は,次によって識別できる。
− パラメタ値
− 幾何的位置
− その両者
これらのうちの少なくとも一つは,曲線の各端点で明記されなければならない。senseによって,円のよ
うな閉曲線のあらゆる区間を明確に定義できる。向き及び順序付けられた端点の組合せによって,円又は
他の閉曲線上の異なる2点を結ぶ,向きのある4個の別々の区間が定義できる。この目的のために,パラ
メタ範囲の循環的な特性が仮定される。例えば,370°は,10°と等価とする。
trimmed̲curveのパラメタ化は,参照される特定のbasis̲curveのパラメタ化から継承される。より正確
には,trimmed̲curveのパラメタsは,basis̲curveのパラメタtから次のとおり得られる。
向きがTRUEの場合は,s=t−t1
向きがFALSEの場合は,s=t2−t
上の式において,t1は,パラメタ1で与えられる値又は点1に対応するパラメタの値とし,t2は,パラ
メタ2で与えられる値又は点2に対応するパラメタの値とする。このtrimmed̲curveでは,パラメタsは,
0から|t2−t1|までの値をとり,s=0が第1のトリム点に対応し,s=|t2−t1|は第2のトリム点に対応する。
備考1. basis̲curveが閉じている場合,向きフラグとの整合性のために,必要に応じてt1又はt2
にbasis̲curveの一周のパラメタ値分だけ加えることもある。
2. (a) sense̲agreement=TRUE,かつt2<t1の場合,t2に一周のパラメタ値を加える。
(b) sense̲agreement=FALSE,かつt1<t2の場合,t1に一周のパラメタ値を加える。
参考 原国際規格では,trim̲1,trim̲2と表記されているが,曲線のトリム点を識別する
parameter̲valueに対応しているので,パラメタ1,パラメタ2とした。幾何位置には,点1,
点2が対応する。
EXPRESSによる定義
*)
ENTITY trimmed̲curve
SUBTYPE OF (bounded̲curve);
44
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
basis̲curve : curve;
trim̲1
: SET[1:2]OF trimming̲select;
trim̲2
: SET[1:2]OF trimming̲select;
sense̲agreement : BOOLEAN;
master̲representation
: trimming̲preference;
WHERE
WR1: (HIINDEX(trim̲1) = 1) XOR (TYPEOF(trim̲1[1]) <>TYPEOF(trim̲1[2]));
WR2: (HIINDEX(trim̲2) = 1) XOR (TYPEOF(trim̲2[1]) <>TYPEOF(trim̲2[2]));
END̲ENTITY;
(*
属性定義
basis̲curve:トリムされるcurve。多重表現をもつ曲線に対して,trim̲1又はtrim̲2として与えられた任意
のparameter̲valueは,basis̲curveのmaster̲representationだけを参照する。
trim̲1:第1のトリム点。cartesian̲point(点1)として,実数のparameter̲value(パラメタ1=t1)として,
又はそれらの両方として特定することができる。
trim̲2:第2のトリム点。cartesian̲point(点2)として,実数のparameter̲value(パラメタ2=t2)として,
又はそれらの両方として特定することができる。
sense̲agreement:trimmed̲curveの方向が,basis̲curveの方向と一致するか,又は反対であるかを表示する
ためのフラグ。
− sense̲agreement=TRUEとなるのは,パラメタの値が増加する方向に曲線を通過する場合。
− sense̲agreement=FALSEとなるのは,それ以外の場合とする。開曲線に対しては,t1>t2ならば,
sense̲agreement=FALSEとする。t2>t1ならば,sense̲agreementにTRUEとする。向きの情報は,開
曲線の場合は冗長となるが,閉曲線に対しては本質的な情報となる。
master̲representation:曲線の端点において,パラメタ及び点の双方がある場合,これは優先形式を示す。
多重表現によって,データが幾何的に同一であることが期待されている場合であっても,複数の形式でデ
ータを交換することが可能になる(4.3.8参照)。
備考 属性master̲representationは,多重形式の同一性を保証することが実用的でないので,優先
形式の表示を許す。これは,データの作成者によって決定される。多重表現をもつエンテ
ィティに対して,パラメタ化,定義域,評価の結果などのすべての特性は,
master̲representationから得られる。他の表現の使用は,実用性への配慮による。
形式的要件
WR1:1個の値がtrim̲1に対して定義されるか,又は2個のトリムの値が異なる型(cartesian̲point及び
parameter̲value)であるかのいずれかとする。
WR2:1個の値がtrim̲2に対して定義されるか,又は2個のトリムの値が異なる型(cartesian̲point及び
parameter̲value)であるかのいずれかとする。
非形式的要件
IP1:trim̲1又はtrim̲2に対して,parameter̲value及びcartesian̲pointの両方が存在する場合,それらは一
致していなければならない。すなわち,parameter̲valueで評価されたbasis̲curveは,指定された
cartesian̲pointと一致していなければならない。
IP2:cartesian̲pointがtrim̲1又はtrim̲2によって指定される場合,それはbasis̲curve上になければならな
45
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い。
IP3:パラメタ1及びパラメタ2の両方が存在する閉じたbasis̲curveの場合を除き,向きのフラグに矛盾
があってはならない。すなわち,sense̲agreementは,パラメタ1<パラメタ2の評価値と等しい。
IP4:パラメタ1及びパラメタ2の両方が存在する場合,パラメタ1とパラメタ2は,等しくない。
IP5:parameter̲valueがtrim̲1又はtrim̲2によって指定される場合,それは,basis̲curveのパラメタ範囲
内になければならない。
4.4.35 composite̲curve composite̲curveは,端点と端点とが結合されている曲線の集まりとする。曲線
の個々のセグメントは,それ自身composite̲curve̲segmentとして定義される。composite̲curveのパラメタ
化は,参照されるbounded̲curveのパラメタ範囲の累算とする。第1セグメントは0からl1までパラメタ
化され,i≧2に対するi番目のセグメントは次のとおりにパラメタ化される。
∑10
−
=
i
k
klから∑
i
k
kl
0
=
まで。
ここで,lkは,k番目のセグメントとなる曲線のパラメタの長さ(パラメタ値の最大値と最小値との差)と
する。Tは,composite̲curveのためのパラメタを表現する。したがって,i番目のセグメントが
reparametarized̲composite̲curve̲segmentでない場合,Tは,i番目のセグメントに対するパラメタti(ti0≦ti
≦ti1)に,次の式で関係付けられる。
segments[i].samesense=TRUEの場合,
∑11
0
−
=
−
+
=
i
k
i
i
k
t
t
l
T
とし,segments[i].samesense=FALSEの場合,
∑11
1
−
=
−
+
=
i
k
i
i
k
t
t
l
T
とする。
segments[i]がreparametarized̲composite̲curve̲segmentの一種の場合は,
∑11
−
=
+
=
i
k
kl
T
τ
とする。ここでτは,4.4.37で定義する。
EXPRESSによる定義
*)
ENTITY composite̲curve
SUBTYPE OF (bounded̲curve);
segments : LIST [1:?] OF composite̲curve̲segment;
self̲intersect
: LOGICAL;
DERIVE
n̲segments : INTEGER := SIZEOF(segments);
closed̲curve
: LOGICAL;
46
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
:= segments[n̲segments].transition <> discontinuous;
WHERW
WR1: ((NOT closed̲curve) AND (SIZEOF(QUERY(temp <* segments |
temp.transition = discontinuous)) = 1)) OR
((closed̲curve) AND (SIZEOF(QUERY(temp <* segments |
temp.transition = discontinuous)) = 0));
END̲ENTITY;
(*
属性定義
n̲segments:構成要素の曲線の個数。
segments:構成要素のbounded̲curve並びにそれらの遷移及び向き。最後のセグメントに対する属性
transitionは,最後のセグメントの終点と最初のセグメントの始点との間の遷移を定義する。この属性
transitionは,値discontinuousをとることが許され,開曲線であることを示す(4.3.2参照)。
self̲intersect:曲線が自己干渉するかどうかの表示。これは,参考とする。
dim:composite̲curveに対する座標空間の次元数。これは,上位型geometric̲representation̲itemから継承
された属性とする。
closed̲curve:曲線が閉じているかどうかの表示。これは,最後のセグメント上のtransitionから得られる。
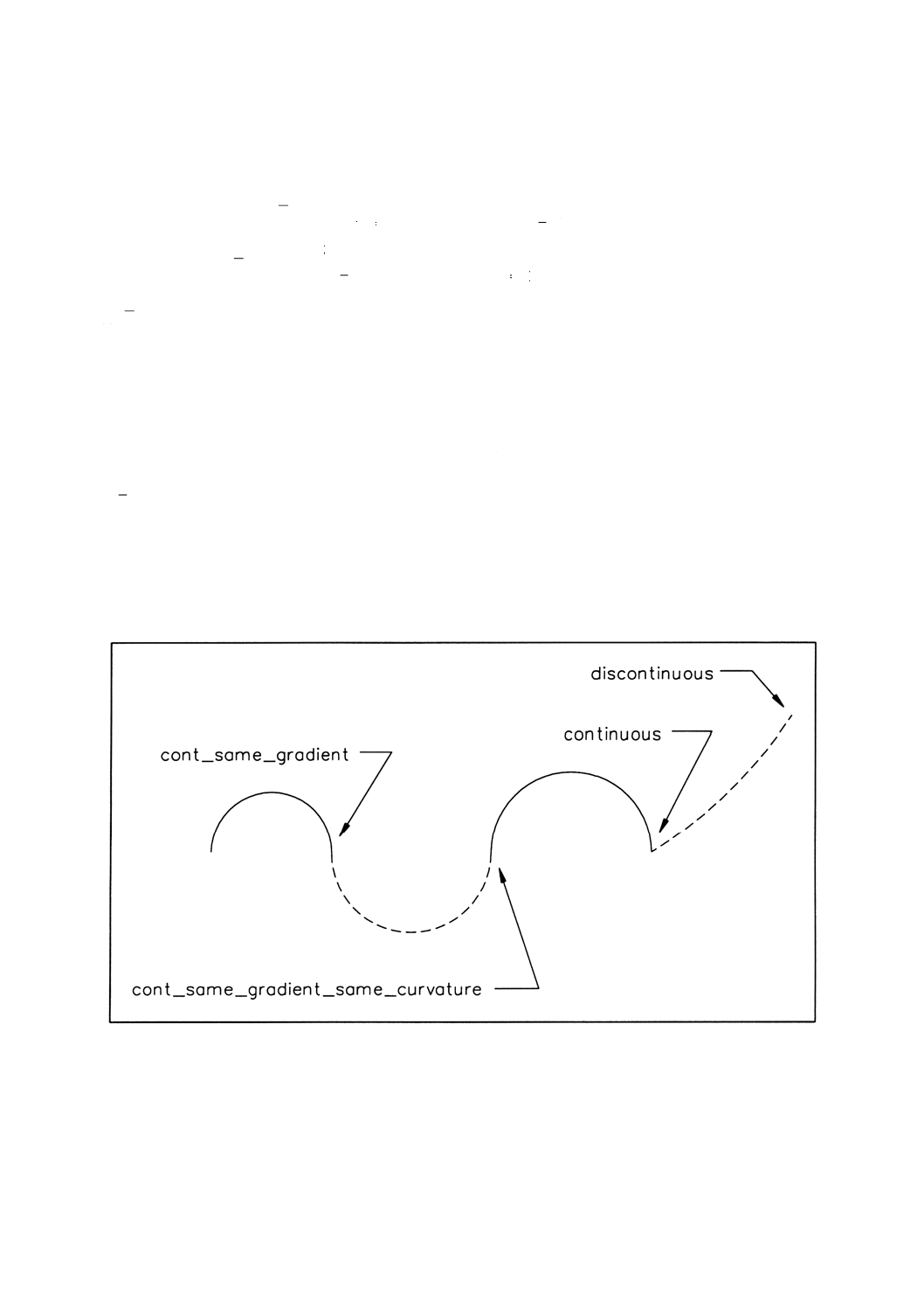
備考 属性についての詳細な情報は,図8参照。
図8 composite̲curve
形式的要件
WR1:開曲線の最後を除いて,transitionは,discontinuousであってはならない。
非形式的要件
IP1:各セグメントの属性same̲senseは,構成要素の曲線の向きを指定する。
same̲senseによって示された方向に通過するとき,セグメント同士は,端点において結合する。
47
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.36 composite̲curve̲segment composite̲curve̲segmentは,composite̲curveを構成するための
bounded̲curveとし,遷移情報をもつ。
EXPRESSによる定義
*)
ENTITY composite̲curve̲segment;
transition : transition̲code;
same̲sense : BOOLEAN;
parent̲curve
: curve;
INVERSE
using̲curves
: BAG[1:?] OF composite̲curve FOR segments;
WHERE
WR1: ('GEOMETRY̲SCHEMA.BOUNDED̲CURVE' IN TYPEOF(parent̲curve));
END̲ENTITY;
(*
属性定義
transition:composite̲curveにおける遷移の状態(このセグメントの最後の点と次のセグメントの最初の点
との幾何的連続性)。
same̲sense:セグメントの向きが,parent̲curveの向きと一致しているか反対であるかの表示。same̲sense
がFALSEの場合,パラメタの値が大きい方の端点を,セグメントの最初の点とする。
parent̲curve:セグメントの幾何を定義するbounded̲curve。
using̲curves:このcomposite̲curve̲segmentをセグメントとして用いるcomposite̲curveの集合。この集合
は,空であってはならない。
形式的要件
WR1:parent̲curveは,bounded̲curveでなければならない。
4.4.37 reparametrised̲composite̲curve̲segment
reparametarized̲composite̲curve̲segment
は
,
composite̲curve̲segmentの特殊な下位型とし,その幾何を変更することなくパラメタの長さを再定義する
ことができる。
param̲lengthをlとおく。
t0≦t≦t1がparent̲curveのパラメタ範囲である場合,reparametarized̲composite̲curve̲segmentのための新
しいパラメタτは,次の式で与えられる。
same̲sense=TRUEの場合,
l
t
t
t
t
0
1
0
−
−
=
τ
とし,same̲sense=FALSEの場合,
l
t
t
t
t
0
1
1
−
−
=
τ
とする。
EXPRESSによる定義
*)
ENTITY reparametrised̲composite̲curve̲segment
48
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SUBTYPE OF (composite̲curve̲segment);
param̲length : parameter̲value;
WHERE
WR1: param̲length > 0.0;
END̲ENTITY;
(*
属性定義
param̲length:セグメントの新しいパラメタの長さ。セグメントには,単純な線形のパラメタ化が与えられ,
最初の点においては0.0となり,最後の点においては,param̲lengthとなる。このセグメントを用いて構成
されるcomposite̲curveのパラメタ化は,param̲lengthによって定義される。
形式的要件
WR1:param̲lengthは,0を超えなければならない。
4.4.38 pcurve pcurveは,曲面のパラメタ空間における2次元曲線によって定義される3次元曲線とする。
曲線が関数 (u,υ)=f(t) によってパラメタ化される場合及び曲面が関数 (x,y,z)=g(u,υ) によってパラメタ化
される場合,pcurveは,関数 (x,y,z)=g(f(t)) によってパラメタ化される。pcurveの定義は,そのbasis̲surface
への参照,及びエンティティdefinitional̲representationを通じての2次元曲線への間接的な参照を含む。こ
の2次元曲線は,パラメタ空間内にあるのでbasis̲surfaceのコンテキストにはない。したがって,直接的
な参照は,不可能である。この2次元曲線において関係する変数は,basis̲surfaceのパラメタ表現のu及
びυであって,デカルト座標のx及びyではない。曲線は,曲面のパラメタ範囲内で定義される。
EXPRESSによる定義
*)
ENTITY pcurve
SUBTYPE OF (curve);
basis̲surface
: surface;
reference̲to̲curve : definitional̲representation;
WHERE
WR1: SIZEOF(reference̲to̲curve\representation.items) = 1;
WR2: 'GEOMETRY̲SCHEMA.CURVE' IN TYPEOF
(reference̲to̲curve\representation.items[1]);
WR3: reference̲to̲curve\representation.items[1]\
geometric̲representation̲item.dim = 2;
END̲ENTITY;
(*
属性定義
basis̲surface:曲線がそのパラメタ空間内において定義されている曲面。
reference̲to̲curve:pcurveを定義するパラメタ空間の曲線への参照。
形式的要件
WR1:reference̲to̲curveに対応するエンティティdefinitional̲representationにおける要素の集合は,ちょう
ど1個の要素をもつ。
WR2:集合の要素は,曲線とする。
49
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WR3:この曲線の次元数は,2とする。
4.4.39 bounded̲pcurve bounded̲pcurveは,pcurveの特殊な下位型とし,bounded̲curveの特性をもつ。
EXPRESSによる定義
*)
ENTITY bounded̲pcurve
SUBTYPE OF (pcurve, bounded̲curve);
WHERE
WR1: ('GEOMETRY̲SCHEMA.BOUNDED̲CURVE' IN
TYPEOF(SELF\pcurve.reference̲to̲curve\representation.items[1]));
END̲ENTITY;
(*
形式的要件
WR1:上位型pcurveが参照する曲線は,bounded̲curveでなければならない。これによって,bounded̲pcurve
の弧長も有限となる。
4.4.40 surface̲curve surface̲curveは,曲面上の曲線とする。この曲線は,3次元空間の曲線(curve̲3d)
として表現される。場合によってpcurveに対応した,曲面の2次元パラメタ空間の曲線としても表現され
る。1個又は2個のpcurve̲or̲surfaceのリストを参照できるので,このエンティティは,単一の曲面上の
曲線か,二つの相異なる曲面か関係する交差のいずれかを定義できる。閉曲面上の“継ぎ目 (seam) ”も,
このエンティティによって表現できる。この場合,各associated̲geometryは,同じ曲面上にあるpcurveと
なる。各pcurveは,それが存在すれば,curve̲3dと同じ向きをもつようにパラメタ化されなければならな
い。surface̲curveのパラメタ化は,属性master̲representationに応じてcurve̲3d又はpcurveから直接得ら
れる。
備考 下位型bounded̲surface̲curveとのANDOR関係からsurface̲curveのインスタンスは,次の
いずれになってもよい。
− surface̲curve
− bounded̲surface̲curve
− intersection̲curve
− intersection̲curve AND bounded̲surface̲curve
− seam̲curve
− seam̲curve AND bounded̲surface̲curve
EXPRESSによる定義
*)
ENTITY surface̲curve
SUPERTYPE OF (ONEOF(intersection̲curve,seam̲curve) ANDOR
bounded̲surface̲curve)
SUBTYPE OF (curve);
curve̲3d
: curve;
associated̲geometry
: LIST[1:2] OF pcurve̲or̲surface;
master̲representation
: preferred̲surface̲curve̲representation;
DERIVE
50
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
basis̲surface : surface
:= associated̲surface(associated̲geometry[1]);
WHERE
WR1: curve̲3d.dim = 3;
WR2: 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(associated̲geometry[1]) OR
(master̲representation <> pcurve̲s1);
WR3: 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(associated̲geometry[2]) OR
(master̲representation <> pcurve̲s2);
WR4: NOT ('GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(curve̲3d));
END̲ENTITY;
(*
属性定義
curve̲3d:surface̲curveの3次元の表現である曲線。
associated̲geometry:surface̲curveに関連付けられる1個又は複数の曲面を定義する1〜2個の
pcurve̲or̲surfaceのリスト。このリストに要素が2個あることは,曲線に2個の曲面が関連付けられるこ
とを示すが,これらの曲線は,相異なる必要はない。pcurveが選択されたとき,それは曲面を識別し,更
にこの曲面のパラメタ空間における曲線も関連付ける。
master̲representation:“優先された”表現の表示。master̲representationは,surface̲curveの一意なパラメ
タ化を決定するための曲線を定義する。master̲representationは,associated̲geometryのリストの中で,3
次元曲線又は第1若しくは第2のpcurveの選択を示すために,それぞれcurve̲3d,pcurve̲s1又はpcurve̲s2
のうちの1個の値をとる。多重表現によって,データが幾何的に全く同一であることが期待されている場
合であっても,複数の形式でデータを交換することが可能となる。
備考 属性master̲representationは,多重形式の同一性を保証することが実用的ではないので,優
先形式の表示を許す。これは,データの作成者によって決定される。多重表現をもつエン
ティティに対して,パラメタ化,定義域,評価の結果などのすべての特性は,
master̲representationから得られる。他の表現の使用は,実用性への配慮による。
basis̲surface:surface̲curveがのっている曲面。これは,associated̲geometryのリストの第1要素から決定
される。
形式的要件
WR1:curve̲3dは,3次元空間で定義される。
WR2:pcurve̲s1は,associated̲geometryのリストの第1要素がpcurveの場合に限り,master̲representation
として選択される。
WR3:pcurve̲s2は,associated̲geometryのリストの第2要素がpcurveの場合に限り,master̲representation
として選択される。このことは,associated̲geometryのリストが1個の要素しか含まない場合には,pcurve̲s2
が選択できないことを示す。
WR4:curve̲3dは,pcurveであってはならない。
非形式的要件
IP1:curve̲3d及び1個以上のpcurveが存在する場合,それらは,数学的には同じ点集合を表現しなけれ
ばならない(すなわち,それらはパラメタ化では異なることが許されるが,幾何的には一致することが必
要となる。)。
51
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IP2:curve̲3d及び任意の関連するpcurveは,それらの向きに関しては一致する。
4.4.41 intersection̲curve intersection̲curveは,2個の曲面の交差から生じる曲線とする。これは,エン
ティティsurface̲curveの特殊な下位型として表現され,リストassociated̲geometryによって定義された2
個の相異なる曲面が関連付けられる。
EXPRESSによる定義
*)
ENTITY intersection̲curve
SUBTYPE OF (surface̲curve);
WHERE
WR1: SIZEOF(SELF\surface̲curve.associated̲geometry) = 2;
WR2: associated̲surface(SELF\surface̲curve.associated̲geometry[1]) <>
associated̲surface(SELF\surface̲curve.associated̲geometry[2]);
END̲ENTITY;
(*
形式的要件
WR1:intersection̲curveは,associated̲geometryの要素をちょうど2個もつ。
WR2:この2個の要素は,異なる曲面に関連付けられる。それらは,intersection̲curveを定義する曲面と
する。
4.4.42 seam̲curve seam̲curveは,閉じたパラメタ曲面上の曲線とし,曲面に対するパラメタ範囲の両端
におけるパラメタが一定の曲線として,2個の異なる表現をもつ。例えば円柱上の“継ぎ目 (seam) ”は,
パラメタ空間において,u=0°又はu=360°の直線としての表現をもつ。
EXPRESSによる定義
*)
ENTITY seam̲curve
SUBTYPE OF (surface̲curve);
WHERE
WR1: SIZEOF(SELF\surface̲curve.associated̲geometry) = 2;
WR2: associated̲surface(SELF\surface̲curve.associated̲geometry[1]) =
associated̲surface(SELF\surface̲curve.associated̲geometry[2]);
WR3: 'GEOMETRY̲SCHEMA.PCURVE' IN
TYPEOF(SELF\surface̲curve.associated̲geometry[1]);
WR4: 'GEOMETRY̲SCHEMA.PCURVE' IN
TYPEOF(SELF\surface̲curve.associated̲geometry[2]);
END̲ENTITY;
(*
形式的要件
WR1:seam̲curveは,associated̲geometryの要素をちょうど2個もつ。
WR2:2個のassociated̲geometryの要素は,同じ曲面に関係付けられる。
WR3:associated̲geometryの第1の要素は,pcurveとする。
WR4:associated̲geometryの第2の要素は,pcurveとする。
52
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.43 bounded̲surface̲curve bounded̲surface̲curveは,surface̲curveの特殊な下位型とし,
bounded̲curveの特性をもつ。
EXPRESSによる定義
*)
ENTITY bounded̲surface̲curve
SUBTYPE OF (surface̲curve, bounded̲curve);
WHERE
WR1: ('GEOMETRY̲SCHEMA.BOUNDED-CURVE' IN
TYPEOF(SELF\surface̲curve.curve̲3d));
END̲ENTITY;
(*
形式的要件
WR1:上位型surface̲curveの属性curve̲3dは,bounded̲curveでなければならない。
4.4.44 composite̲curve̲on̲surface composite̲curve̲on̲surfaceは,curve̲on̲surfaceであるセグメントを
集めたものとする。各セグメントは,basis̲surface上にあることか必要で,次のいずれかとする。
− surface̲curve
− intersection̲curve
− composite̲curve̲on̲surface
備考 composite̲curve̲on̲surfaceは,bounded̲curveの下位型であるので,composite̲curve̲segment
の属性parent̲curveとして含まれることを可能にする。
隣接するセグメント間には,少なくとも位置的な連続性を必要とする。composite̲curveのパラメタ化は,
セグメントのパラメタ範囲の累算から得られる。第1セグメントは,0からl1までパラメタ化され,i≧2
に対するi番目のセグメントは,次のとおりにパラメタ化される。
∑10
−
=
i
k
klから∑
i
k
kl
0
=
まで。
ここで,lkは,k番目の曲線セグメントのパラメタの長さ(パラメタ値の最大値と最小値との差)とする。
EXPRESSによる定義
*)
ENTITY composite̲curve̲on̲surface
SUPERTYPE OF (boundary̲curve)
SUBTYPE OF (composite̲curve);
DERIVE
basis̲surface : SET[0:2] OF surface :=
get̲basis̲surface(SELF);
WHERE
WR1: SIZEOF(basis̲surface) > 0;
WR2: constraints̲composite̲curve̲on̲surface(SELF);
END̲ENTITY;
(*
53
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
属性定義
basis̲surface:composite̲curveがのっている曲面。
SELF\composite̲curve.n̲segments:構成要素の曲線の個数。
SELF\composite̲curve-segments:構成要素のbounded̲curve,それらの遷移及び向き。最後のセグメント
に対する遷移は,最後のセグメントの終点と最初のセグメントの始点との間の遷移を定義する。この要素
は,値discontinuousをとることが許され,それは開曲線を示す(4.3.2参照)。
SELF\composite̲curve.self̲intersect:曲線が自己干渉するかどうかの表示。
SELF\composite̲curve.dim:composite̲curveに対する座標空間の次元数。
SELF\composite̲curve.closed̲curve:曲線が閉じているかどうかの表示。
形式的要件
WR1:集合basis̲surfaceは,少なくとも一つの曲面を含まなければならない。これによって,すべてのセ
グメントが,同じ曲面の上の曲線を参照できる。
WR2:各セグメントは,pcurve,surface̲curve又はcomposite̲surface̲on̲curveを参照する。
非形式的要件
IP1:セグメントcomposite̲curve̲on̲surfaceによって参照される各parent̲curveは,curve̲on̲surface又は
bounded̲curveとする。
4.4.45 offset̲curve̲2d offset̲curve̲2dは,2次元空間内において,基礎となる曲線(basis̲curve)からの距
離が一定の曲線とする。basis̲curveのある平面内において,basis̲curveの法線に沿ってdistanceだけオフ
セットすることによって,このエンティティは,単純な平面内オフセット曲線を定義する。
基礎となる曲線は,その上のすべての点において,適切な接線方向をもたなければならない。
composite̲curveの場合は,各セグメント間のtransition̲codeは,cont̲same̲gradient又は
cont̲same̲gradient̲same̲curvatureとする。
備考 offset̲curve̲2dは,basis̲curveと異なるcurveであってもよい。自己干渉していない曲線の
オフセットは,自己干渉する可能性がある。連続曲線のオフセットは,不連続にならない
ように注意しなければならない。
offset̲curve̲2dは,そのパラメタ化をbasis̲curveから得る。offset̲curve̲2dは,次のとおりパラメタ化さ
れる。
λ(u)=C(u)+d(orthogonal̲complement(T))
ここで,Tはパラメタ値uにおけるbasis̲curve C(u)への単位接ベクトルとし,dはdistanceとする。基礎
となる曲線は,2次元とする。
EXPRESSによる定義
*)
ENTITY offset̲curve̲2d
SUBTYPE OF (curve);
basis̲curve
: curve;
distance : length̲measure;
self̲intersect
: LOGICAL;
WHERE
WR1: basis̲curve.dim = 2;
END̲ENTITY;
54
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(*
属性定義
basis̲curve:オフセットされるcurve。
distance:basis̲curveからオフセット曲線への距離。distanceは,正,負又は0であることが許される。distance
の正の値は,与えられた点における接ベクトルTを反時計回りに90°回転した向きで曲線と直交する方向
に,オフセットを定義する(これは,orthogonal̲complement(T)の方向とする。)。
self̲intersect:オフセット曲線が自己干渉するかどうかの表示。これは,参考とする。
形式的要件
WR1:基礎となる曲線は,2次元空間内で定義される。
4.4.46 offset̲curve̲3d offset̲curve̲3dは,3次元空間内において,基礎となる曲線 (basis̲curve) からの
距離が一定の曲線とする。
基礎となる曲線は,あらゆる点において,明確な接線方向をもたなければならない。composite̲curveの
場合は,各セグメント間のtransition̲codeは,cont̲same̲gradient又はcont̲same̲gradient̲same̲curvature
とする。
basis̲curve上の任意の点(パラメタ)におけるオフセソト曲線は,V×Tの方向にある。ここで,Vは,
固定された参照方向とし,Tは,basis̲curveへの単位接線とする。オフセット方向が明確であるためには,
曲線の任意の点において,TがVと同じ又は反対の方向にあることが許されない。
備考 offset̲curve̲3dは,basis̲curveと異なるcurveであってもよい。自己干渉していない曲線の
オフセットが自己干渉する可能性がある。連続曲線のオフセットは,不連続にならないよ
うに注意しなければならない。
offset̲curve̲3dは,そのパラメタ化をbasis̲curveから得る。offset̲curve̲3dは,次のとおりパラメタ化さ
れる。
λ(u)=C(u)+dV×T
ここで,Tはパラメタ値uにおけるbasis̲curveC(u)への単位接ベクトルとし,dはdistanceとする。
EXPRESSによる定義
*)
ENTITY offset̲curve̲3d
SUBTYPE OF (curve);
basis̲curve
: curve;
distance : length̲measure;
self̲intersect
: LOGICAL;
ref̲direction
: direction;
WHERE
WR1: (basis̲curve.dim = 3) AND (ref̲direction.dim = 3);
END̲ENTITY;
(*
属性定義
basis̲curve:オフセットされるcurve。
distance:basis̲curveからオフセット曲線への距離。distanceは,正,負又は0であることが許される。
self̲intersect:オフセット曲線が自己干渉するかどうかの表示。これは,参考とする。
55
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ref̲direction:basis̲curveからオフセット曲線の方向を定義するために使われるdirection。
形式的要件
WR1:基礎となる曲線及び参照方向は,ともに3次元空間内で定義される。
非形式的要件
IP1:曲線上のすべての点において,ref̲directionが接ベクトルの方向と平行又は逆向きの平行であること
は許されない。
4.4.47 curve̲replica curve̲replicaは,異なる配置における曲線の複製(replica)とする。これは,
parent̲curve及びtransformationを参照することによって定義される。生成される曲線の幾何形状は,
parent̲curveのものと同一となる。しかし,transformationが拡大・縮小を含む場合,大きさが異なること
になる。curve̲replicaは,そのパラメタ範囲及びパラメタ化を,直接parent̲curveから得る。parent̲curve
がcurve̲on̲surfaceの場合,一般的に,複製は,曲面上にあるという特性を共有しない。
EXPRESSによる定義
*)
ENTITY curve̲replica
SUBTYPE OF (curve);
parent̲curve
: curve;
transformation
: cartesian̲transformation̲operator;
WHERE
WR1: transformation.dim = parent̲curve.dim;
WR2: acyclic̲curve̲replica(SELF,parent̲curve);
END̲ENTITY;
(*
属性定義
parent̲curve:複製される曲線。
transformation:curve̲replicaの配置を定義するcartesian̲transformation̲operator。この変換は,拡大・縮小
を含むことが許される。
形式的要件
WR1:属性transformationの座標空間の次元数は,parent̲curveのそれと等しくなければならない。
WR2:curve̲replicaは,自身の定義に関係してはならない。
4.4.48 surface 定義は,3.1による。surface(曲面)は,3次元空間における,局所的には2次元の連結
点集合と考えることができる。surfaceは,多様体でなくてもよい。surfaceは,単一の点,又は一部若しく
は全体が曲線であってはならない。
各surfaceは,パラメタ表現の形式
σ(u,v)
をもつ。ここで,u及びυは,独立な無次元のパラメタとする。曲面上のすべての点において,単位法線ベ
クトルNは,次の式で与えられる。
v
u
v
u
∂
∂
×
∂
∂
σ
σ
N
=
)
,
(
EXPRESSによる定義
*)
56
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ENTITY surface
SUPERTYPE OF (ONEOF(elementary̲surface, swept̲surface, bounded̲surface,
offset̲surface, surface̲replica))
SUBTYPE OF (geometric̲representation̲item);
END̲ENTITY;
(*
非形式的要件
IP1:surfaceの面積は,0ではない。
IP2:surfaceは,弧状連結とする。
4.4.49 elementary̲surface elementary̲surfaceは,パラメタ表現の定義をもつ単純な解析曲面とする。
EXPRESSによる定義
*)
ENTITY elementary̲surface
SUPERTYPE OF (ONEOF(plane, cylindrical̲surface, conical̲surface,
spherical̲surface, toroidal̲surface))
SUBTYPE OF (surface);
position : axis2̲placement̲3d;
END̲ENTITY;
(*
属性定義
position:elementary̲surfaceの配置及び向き。この属性は,曲面のパラメタ化の定義に使用される。
4.4.50 plane plane(平面)は,一定の法線をもった境界のないsurfaceとする。planeは,plane上の点及
びplaneの法線の方向によって定義する。データは,次のとおり解釈される。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]=planeの法線
パラメタ化は,次のとおりとする。
σ(u,v)=C+xu+yv
パラメタ範囲は,−∞<u,υ<∞とする。上のパラメタ化では,単位ベクトルのx及びyの長さの単位は,
planeのコンテキストから得られる。
EXPRESSによる定義
*)
ENTITY plane
SUBTYPE OF (elementary̲surface);
END̲ENTITY;
(*
属性定義
SELF\elementary̲surface.position:surfaceの配置及び向き。この属性は,上位型のelementary̲surfaceから
継承される。
57
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SELF\elementary̲surface.position.location:plane上の点。
SELF\elementary̲surface.position.p[3]:このdirectionは,SELF\elementary̲surface.position.axisに等しく,
planeの法線を定義する。
4.4.51 cylindrical̲surface cylindrical̲surface(円柱面)は,直線から一定の距離 (radius) にある曲面とす
る。
cylindrical̲surfaceは,半径,向き及び配置から定義される。データは,次のとおり解釈される。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=radius
パラメタ化は,次のとおりとする。
σ(u,v)=C+R(cosu)x+(sinu)y)+vz
ここで,パラメタ範囲は,0°≦u≦360°及び−∞<υ<∞とする。上のパラメタ化では,単位ベクトルz
の長さの単位は,radiusのものと等しい。
上で定義された配置座標系において,曲面は,式S=0で表現される。ここで,
S(x,y,z)=x2+y2−R2
とする。曲面上のすべての点について,曲面の法線の正の方向は,次のとおり与えられる。
(Sx,Sy,Sx)
単位法線ベクトルは,次の式から求まる。
N(u,v)=(cosu)x+(sinu)y
この法線の向きは,円柱の軸から離れる向きとなる。
EXPRESSによる定義
*)
ENTITY
cylindrical̲surface
SUBTYPE OF (elementary̲surface);
radius : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\elementary̲surface.position:cylindrical̲surfaceの配置及び向き。
SELF\elementary̲surface.position.location:cylindrical̲surfaceの軸上の点。
SELF\elementary̲surface.position.p[3]:cylindrical̲surfaceの軸の方向。
radius:cylindrical̲surfaceの半径。
4.4.52 conical̲surface conical̲surface(円錐面)は,3次元空間の直線を,それと交差する任意の直線の
回りで回転することによって生成される曲面とする。conical̲surfaceは,半頂角,配置,及び向きと,円
錐の軸に垂直で配置点Cを通る平面上における半径とによって定義される。
備考 この表現形式は,配置点Cの近くで最大の幾何的精度を与えるように定められた。このた
め,頂点を配置点とするのは,頂点に近い領域か対象となるときに限った方がよい。
58
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
データは,次のとおり解釈される。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=radius
α=semi̲angle
パラメタ化は,次のとおりとする。
σ(u,v)=C+(R+υtanα)((cosu)x+(sinu)y)+vz
ここで,パラメタ範囲は,0°≦u≦360°及び-∞<υ<∞とする。上のパラメタ化では,単位ベクトルz
の長さの単位は,radiusのものと等しい。
上で定義された配置座標系において,曲面は,式S=0で表現される。ここで,
S(x,y,z)=x2+y2−(R+ztanα)2
とする。曲面上のすべての点において,曲面の法線の正の方向は,次のとおり与えられる。
(Sx,Sy,Sz)
単位法線ベクトルは,次の式から求まる。
2)
(tan
1
)
(tan
)
(sin
)
(cos
)
,
(
α
α
+
−
+
=
z
y
x
N
u
u
v
u
この法線の向きは,円錐の軸から離れる向きとなる。半径が0のときは,円錐の頂点は,配置座標系の点
(0,0,0)(すなわち,SELF\elementary̲surface.position.location)にあるとする。
EXPRESSによる定義
*)
ENTITY
conical̲surface
SUBTYPE OF (elementary̲surface);
radius
: length̲measure;
semi̲angle : plane̲angle̲measure;
WHERE
WR1: radius >= 0.0;
END̲ENTITY;
(*
属性定義
SELF\elementary̲surface.position:surfaceの配置及び向き。
SELF\elementary̲surface.position.location:conical̲surfaceの軸上の配置点。
SELF\elementary̲surface.position.p[3]:conical̲surfaceの軸の方向。
radius:配置点(すなわち,SELF\elementary̲surface.position.location)を通り,conical̲surfaceの軸に垂直
な平面と,このconical̲surfaceとの交線である円の半径。
semi̲angle:conical̲surfaceの半頂角。
備考 属性の詳細は,図9参照。
形式的要件
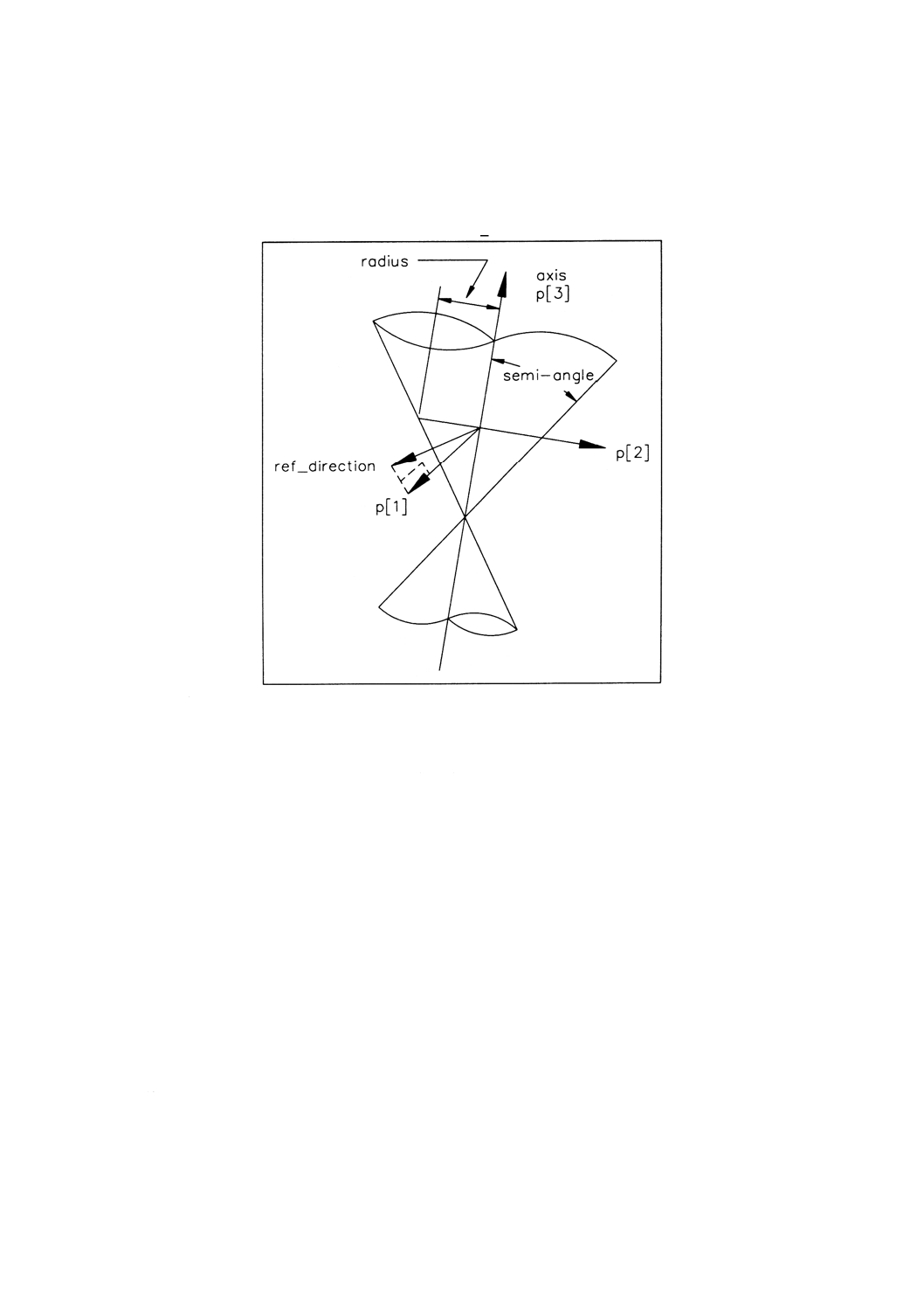
59
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WR1:半径は,負になってはならない。
非形式的要件
IP1:半頂角は,0°を超え90°未満とする。
図9 comical̲surface
4.4.53 spherical̲surface spherical̲surface(球面)は,中心点から一定の距離(radius)にある曲面とする。
spherical̲surfaceは,曲面の半径,配置及び向きから定義される。
データは,次のとおり解釈される。
C=position.location(中心)
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=radius
パラメタ化は,次のとおりとする。
σ(u,v)=C+Rcosv((cosu)x+(sinu)y)+R(sinv)z
ここでパラメタ範囲は,0°≦u≦360°及び-90°≦υ≦90°とする。
上で定義された配置座標系において,曲面は,式S=0で表現される。ここで,
S(x,y,z)=x2+y2+z2−R2
とする。曲面上のすべての点について,曲面の法線の正の方向は,次のとおり与えられる。
(Sx,Sy,Sz)
単位法線ベクトルは,次の式から求まる。
N(u,v)=cosv((cosu)x+(sinu)y)+(sinv)z
すなわち,球の中心から離れる向きとなる。
60
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRIESSによる定義
*)
ENTITY spherical̲surface
SUBTYPE OF (elementary̲surface);
radius : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\elementary̲surface.position:spherical̲surfaceの配置及び向き。
SELF\elementary̲surface.position.location:球の中心。
radius:spherical̲surfaceの半径。
4.4.54 toroidal̲surface toroidal̲surface(輪環面)は,円を,それと同平面の直線の回りで回転すること
によって生成される曲面とする。回転する円の半径を,ここではminor̲radiusと呼び,major̲radiusは,円
の中心から回転軸までの距離とする。toroidal̲surfaceは,major̲radius及びminor̲radiusと曲面の位置及び
向きとによって定義される。
データは,次のとおり解釈される。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=major̲radius
r=minor̲radius
パラメタ化は,次のとおりとする。
σ(u,v)=C+(R+rcosv)((cosu)x+(sinu)y)+r(sinv)z
ここで,パラメタ範囲は,0°≦u,υ≦360°とする。
上で定義された配置座標系において,曲面は,式S=0で表現される。ここで,
S(x,y,z)=x2+y2+z2−2R
2
2y
x+
−r2+R2
とする。曲面上のすべての点において,曲面の法線の正の方向は,次のとおり与えられる。
(Sx,Sy,Sz)
単位法線ベクトルは,次の式から求まる。
N(u,v)=cosv((cosu)x+(sinu)y)+(sinv)z
この法線の向きは,半径がRで中心がCの円上で最も近い点から離れる向きとなる。major̲radiusが
minor̲radiusよりも大きい場合,多様体曲面となる。それ以外の場合,曲面は,自己干渉する。
参考 原国際規格の表現では,法線の向きが寸理解しにくいが,次の参考図のように解釈すると
よい。
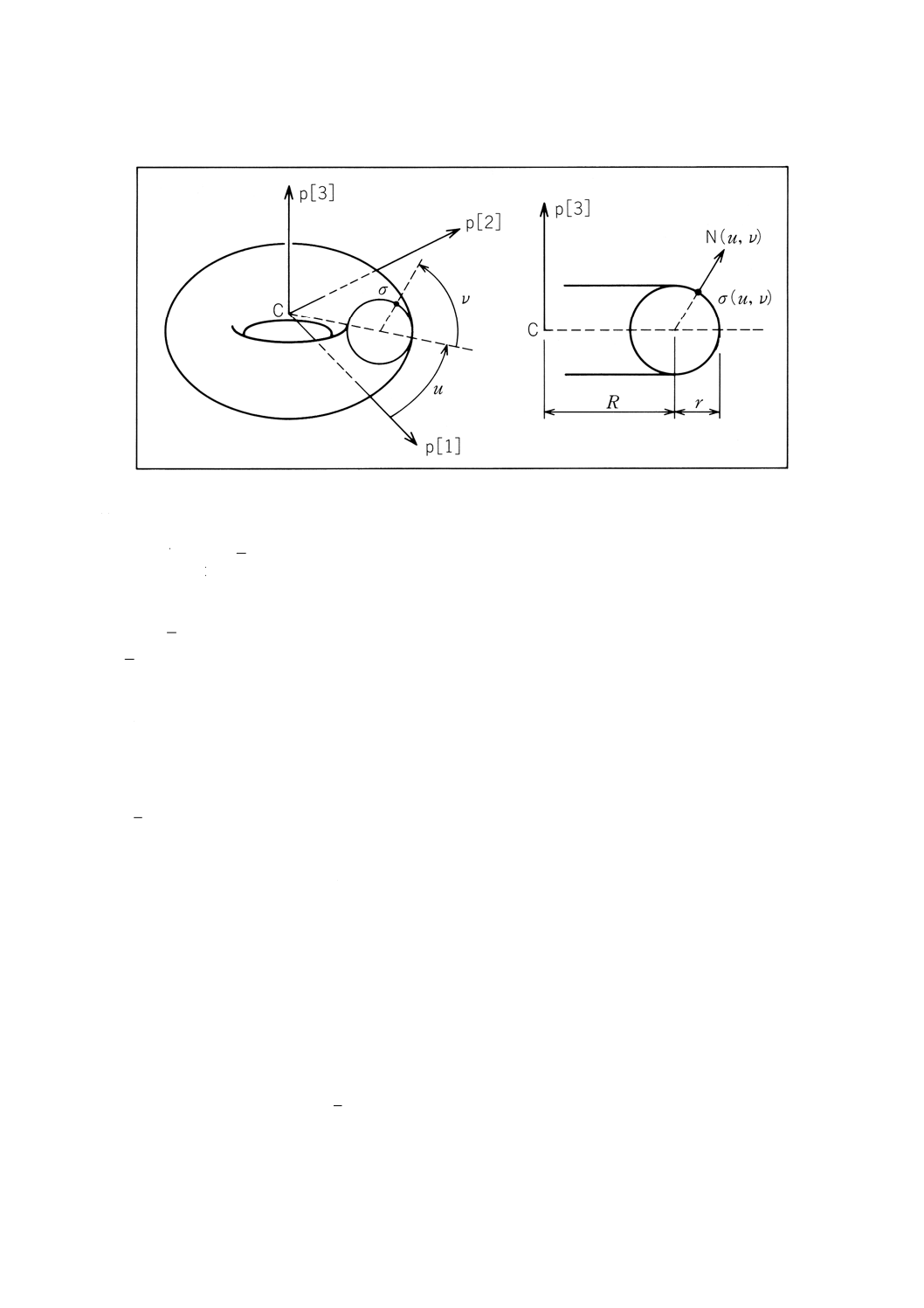
61
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図 toroidal̲surfaceの法線の向き
EXPRESSによる定義
*)
ENTITY toroidal̲surface
SUBTYPE OF (elementary̲surface);
major̲radius : positive̲length̲measure;
minor̲radius : positive̲length̲measure;
END̲ENTITY;
(*
属性定義
SELF\elementary̲surface.position:toroidal̲surfaceの配置及び向き。
SELF\elementary̲surface.position.location:輪環体の中心点。
major̲radius:輪環体の長半径。
minor̲radius:輪環体の短半径。
4.4.55 degenerate̲toroidal̲surface degenerate̲toroidal̲surfaceは,toroidal̲surfaceの特別な下位型とし,
minor̲radiusがmajor̲radiusより大きい曲面とする。この下位型においては,多様体曲面を定義するために,
パラメタ範囲が制限される。この多様体曲面は,上位型によって定義される自己干渉する曲面の,内側の
“レモン形”をした部分,又は外側の“リンゴ形”をした部分のいずれかになる。
データは,次のとおり解釈される。
C=position.location
x=position.p[1]
y=position.p[2]
z=position.p[3]
R=major̲radius
r=minor̲radius
パラメタ化は,次のとおりとする。
σ(u,v)=C+(R+rcosv)((cosu)x+(sinu)y)+r(sinv)z
62
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで,パラメタ範囲は,次のとおりとする。
select̲outer=TRUEのとき
0°≦u≦360°
−φ≦v≦φ
select̲outer=FALSEのとき
0°≦u≦360°
φ≦v≦360°−φ
ここでφは,rcosφ=-Rで与えられる角度(°)とする。
EXPRESSによる定義
*)
ENTITY degenerate̲toroidal̲surface
SUBTYPE OF (toroidal̲surface);
select̲outer : BOOLEAN;
WHERE
WR1: major̲radius < minor̲radius;
END̲ENTITY;
(*
属性定義
select̲outer:degenerate̲toroidal̲surfaceの二つの部分を区別するブール型のフラグ。select̲outerがTRUE
のとき,曲面の外側部分が選ばれて,“リンゴ形”をした軸対称の閉曲面が定義される。select̲outerが
FALSEのとき,曲面の内側部分が選ばれて,“レモン形”をした軸対称の閉曲面が定義される。
形式的要件
WR1:major̲radiusは,minor̲radiusより小さい。
4.4.56 swept̲surface swept̲surfaceは,ある曲線を他の曲線に沿って掃引することによって作られる。
EXPRESSによる定義
*)
ENTITY swept̲surface
SUPERTYPE OF (ONEOF(surface̲of̲linear̲extrusion, surface̲of̲revolution))
SUBTYPE OF (surface);
swept̲curve : curve;
END̲ENTITY;
(*
属性定義
swept̲curve:swept̲surfaceを定義する際に掃引されるcurve。swept̲curveがpcurveのとき,これは,その
pcurveの2次元パラメタ空間内の曲線ではなく,掃引される3次元幾何空間内でのcurveの像とする。
4.4.57 surface̲of̲linear̲extrusion この曲面は,単純なswept̲surface,すなわち,与えられた方向に曲線
を掃引して得られる一般化された柱状の曲面とする。パラメタ化は,次のとおりとする。ただし,曲線の
パラメタ化は,λ(u)による。
V=extrusion̲axis
σ(u,v)=λ(u)+vV
63
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
υのパラメタ範囲は,-∞<υ<∞とし,uのパラメタ範囲は,曲線のパラメタ化によって定義する。
EXPRESSによる定義
*)
ENTITY surface̲of̲linear̲extrusion
SUBTYPE OF (swept̲surface);
extrusion̲axis : vector;
END̲ENTITY;
(*
属性定義
extrusion̲axis:掃引の方向。このベクトルの大きさによって,パラメタ化が決まる。
SELF\swept̲surface.swept̲curve:掃引されるcurve。
非形式的要件
IP1:surface̲of̲linear̲extrusionは,自己干渉しない。
4.4.58 surface̲of̲revolution surface̲of̲revolutionは,曲線をある軸の回りに1回転して得られる曲面と
する。
データは,次のとおり解釈される。
パラメタ化は,次のとおりとする。ただし,曲線のパラメタ化は,λ(υ)による。
C=position.location
V=position.z
σ(u,υ)=C+(λ(v)−C)cosu+((λ(v)−C)・V)V(1−cosu)+V×(λ(v)−C)sinu
この曲線を1回転することによって得られる曲線が単一値曲面となるためには,Cを中心としVを軸とす
る円柱座標系 (r,φ,z) でその曲線を表した場合,曲線上のパラメタ値の異なる2点が同じ (r,z) をもっては
ならない。
備考 ここで,単一値曲面は,そのパラメタ範囲に対応するパラメタ空間内の長方形の内部から
幾何空間への,曲面の式によって定義される写像が,一対一対応である曲面とする。
surface̲of̲revolutionのパラメタ範囲は,0°≦u≦360°とする。
υのパラメタ範囲は,参照される曲線によって定義される。
備考 曲面の幾何形状は,曲線のパラメタ化に依存しない。
EXPRESSによる定義
*)
ENTITY surface̲of̲revolution
SUBTYPE OF (swept̲surface);
axis̲position : axis1̲placement;
DERIVE
axis̲line : line := line(axis̲position.location,
vector(axis̲position.z, 1.0));
END̲ENTITY;
(*
属性定義
axis̲position:回転軸上の点及び回転軸の方向。
64
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SELF\swept̲surface.swept̲curve:axis̲lineの回りに回転されるcurve。
axis̲line:回転軸に一致するline。
非形式的要件
IP1:surface̲of̲revolutionは,自己干渉してはならない。
IP2:swept̲curveは,どの有限長さ部分においても,axis̲lineと一致してはならない。
4.4.59 bounded̲surface bounded̲surfaceは,同定可能な境界をもつ有限領域の曲面とする。
EXPRESSによる定義
*)
ENTITY bounded̲surface
SUPERTYPE OF (ONEOF(b̲spline̲surface, rectangular̲trimmed̲surface,
curve̲bounded̲surface, rectangular̲composite̲surface))
SUBTYPE OF (surface);
END̲ENTITY;
(*
非形式的要件
IP1:bounded̲surfaceの面積は,0でなくかつ有限とする。
IP2:bounded̲surfaceは,境界曲線をもつ。
4.4.60 b̲spline̲surface b̲spline̲surface(B-スプライン曲面)は,制御点,基底関数及び(場合によって
は)重みによって定義される有理式又は多項式の,パラメタ曲面の一般的な形式とする。このエンティテ
ィは,b̲spline̲curveと同様に,データの幾つかを導出できる特別な下位型をもつ。
備考1. b̲spline̲surfaceの暗黙値及び下位型の識別は,性能の考慮のために及び計算の実行にお
ける効率に関して重要である。
2. B-スプラインが有理であるとは,重みの中に等しくないものが存在することをいう。多
項式ならば,重みは,すべて暗黙で1にしてもよい。
3. b̲spline̲surfaceが一様,準一様又は区分的ベジエの場合,ノット及びノット多重度は,
暗黙にしてもよい(すなわち,属性定義によって指定されたデータが存在しなくてもよ
い。)。ノットを暗黙値にする場合,離れたノットの間の差は,1.0が仮定され,その曲面
の有効なパラメタ範囲は,0.0から始まる。これらの暗黙値は,下位型が与える。
4. 非一様の場合には,ノット及びノット多重度は,暗黙にしてはならない。
5. 重み及びノットの暗黙化は,互いに独立に行われる。
データは,次のとおり解釈する。
(a) ここで使用される記号は,次のとおりとする。
K1=制御点のu方向の添字の上限
K2=制御点のυ方向の添字の上限
Pij=制御点
wij=重み
d1=u方向の次数
d2=υ方向の次数
(b) 制御点は,次のとおり順序付けられる。
P00, P01, P02, ……,PK1(K2-1),PK1K2
65
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
有理の場合,重みも同様に順序付けられる。
(c) sがパラメタu又はパラメタυのいずれかを表すとき,kを制御点の添字の上限とし,dをsに対する
次数とすると,ノット配列は, (k+d+2) 個の実数 [s−d,…,sk+1] の配列となる。ただし, [−d,k]
の範囲のすべての添字jについてsj≦sj+1とする。この配列は,リストu̲knots又はv̲knotsから,多重
度に応じて各多重ノットを繰り返すことで得られる。i番目の次数dの正規化されたB-スプライン基
底関数
id
Nは,この配列の部分集合 [si−d, …,si+1] 上で定義される。
(d) Lをノットリスト中で値の異なるものの個数とする。Lは,“ノットの添字の上限 (knot̲u̲upper,
knot̲v̲upper) ”として参照される。mjをj番目の異なるノット値の多重度(繰返しの数)とする。こ
の場合,次のとおりとなる。
∑
L
i
i
k
d
m
1
2
=
+
+
=
すべてのノット多重度は,最初及び最後を除き,1〜dの範囲になければならない。最初のもの及び
最後のものは,最大でd+1をとることができる。基底関数の値を求める場合,例えば,多重度3のノ
ットuは,ノット配列における並びu,u,uとして解釈される。
(e) surface̲formは,特定の2次曲面(次数は2),線織面及びsurface̲of̲revolutionを識別するために用い
られる。b̲spline̲curveと同様,surface̲formは参考とし,曲面のデータが優先される。
(f) 曲面は,次のとおり解釈される。多項式のとき,曲面は,次の式で与えられる。
∑∑
1
0
2
0
2
1
)
(
)
(
)
,
(
K
i
K
j
dj
di
ij
v
N
u
N
v
u
=
=
=
P
σ
有理式のとき,曲面の式は,次のとおりとする。
∑∑
∑∑
1
0
2
0
2
1
1
0
2
0
2
1
)
(
)
(
)
(
)
(
)
,
(
K
i
K
j
dj
di
ij
K
i
K
j
dj
di
ij
ij
v
N
u
N
w
v
N
u
N
w
v
u
=
=
=
=
=
P
σ
備考 B-スプライン基底関数の
1
di
N(u)及び
2
di
N
(υ)の定義は,附属書E(参考)のE1〜E3による。こ
れらの参考文献における用語の違いには,注意を要する。
EXPRESSによる定義
*)
ENTITY b̲spline̲surface
SUPERTYPE OF (ONEOF(b̲spline̲surface̲with̲knots, uniform̲surface,
quasi̲uniform̲surface, bezier̲surface)
ANDOR rational̲b̲spline̲surface)
SUBTYPE OF (bounded̲surface);
u̲degree
: INTEGER;
v̲degree
: INTEGER;
control̲points̲list
: LIST [2:?]OF
LIST [2:?]OF cartesian̲point;
surface̲form
: b̲spline̲surface̲form;
u̲closed
: LOGICAL;
66
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
v̲closed
: LOGICAL;
self̲intersect
: LOGICAL;
DERIVE
u̲upper
: INTEGER := SIZEOF(control̲points̲list) -1;
v̲upper
: INTEGER := SIZEOF(control̲points̲list[1]) -1;
control̲points : ARRAY [0:u̲upper]OF ARRAY [0:v̲upper]OF
cartesian̲point
:= make̲array̲of̲array(control̲points̲list,
0,u̲upper,0,v̲upper);
WHERE
WR1: ('GEOMETRY̲SCHEMA.UNIFORM̲SURFACE' IN TYPEOF(SELF)) OR
('GEOMETRY̲SCHEMA.QUASI̲UNIFORM̲SURFACE' IN TYPEOF(SELF)) OR
('GEOMETRY̲SCHEMA.BEZIER̲SURFACE' IN TYPEOF(SELF)) OR
('GEOMETRY-SCHEMA.B̲SPLINE̲SURFACE̲WITH̲KNOTS' IN TYPEOF(SELF));
END̲ENTITY;
(*
属性定義
u̲degree:uに関する基底関数の代数的な次数。
v̲degree:υに関する基底関数の代数的な次数。
control̲points̲list:制御点のリストのリスト。
surface̲form:特定の曲面形式の識別子(4.3.5参照)。
u̲closed:u方向で曲面が閉じているかどうかの表示。これは,参考とする。
v̲closed:υ方向で曲面が閉じているかどうかの表示。これは,参考とする。
self̲intersect:曲面が自己干渉するかどうかを示すフラグ。これは,参考とする。
u̲upper:u方向での制御点の添字の上限。
v̲upper:υ方向での制御点の添字の上限。
control̲points:曲面の幾何を定義する制御点の(2次元)配列。これは,control̲points̲listから導出される。
形式的要件
WR1:このエンティティのインスタンス化は,下位型のb̲spline̲surface̲with̲knots, uniform̲surface,
quasi̲uniform̲surface又はbezier̲surfaceのうちの1個でなければならない。
4.4.61 b̲spline̲surface̲with̲knots これは,ノット値か明示的に与えられたb̲spline̲surfaceとする。こ
の下位型は,非一様なb̲spline̲surfaceを表現するために用いるか,他のknot̲typeのために用いてもよい。
すべてのノット多重度は,最初のもの及び最後のものを除き,1〜dの範囲になければならない。最初の
もの及び最後のものは,最大でd+1をとることかできる。
基底関数の値を求める場合,例えば,多重度3のノットuは,ノット配列における並びu,u,uとして解釈
される。
EXPRESSによる定義
*)
ENTITY b̲spline̲surface̲with̲knots
SUBTYPE OF (b̲spline̲surface);
67
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
u̲multiplicities
: LIST [2:?]OF INTEGER;
v̲multiplicities
: LIST [2:?]OF INTEGER;
u̲knots
: LIST [2:?]OF parameter̲value;
v̲knots : LIST [2:?]OF parameter̲value;
knot̲spec
: knot̲type;
DERIVE
knot̲u̲upper
: INTEGER := SIZEOF(u̲knots);
knot̲v̲upper
: INTEGER := SIZEOF(v̲knots);
WHERE
WR1: constraints̲param̲b̲spline(SELF\b̲spline̲surface.u̲degree,
knot̲u̲upper, SELF\b̲spline̲surface.u̲upper,
u̲multiplicities, u̲knots);
WR2: constraints̲param̲b̲spline(SELF\b̲spline̲surface.v̲degree,
knot̲v̲upper, SELF\b̲spline̲surface.v̲upper,
v̲multiplicities, v̲knots);
WR3: SIZEOF(u̲multiplicities) = knot̲u̲upper;
WR4: SIZEOF(v̲multiplicities) = knot̲v̲upper;
END̲ENTITY;
(*
属性定義
u̲multiplicities:u方向でのノットの多重度。
v̲multiplicities:υ方向でのノットの多重度。
u̲knots:u方向での相異なるノットのリスト。
v̲knots:υ方向での相異なるノットのリスト。
knot̲spec:ノットの種類の記述。
knot̲u̲upper:u方向での相異なるノットの個数。
knot̲v̲upper:υ方向での相異なるノットの個数。
SELF\b̲spline̲surface.u̲degree:uに関する基底関数の代数的な次数。
SELF\b̲spline̲surface.v̲degree:υに関する基底関数の代数的な次数。
SELF\b̲spline̲surface.control̲points̲list:制御点のリストのリスト。
SELF\b̲spline̲surface.surface̲form:特定の曲面形状の識別子(詳細は,4.3.5参照)。
SELF\b̲spline̲surface.u̲closed:u方向で曲面が閉じているかどうかの表示。これは,参考とする。
SELF\b̲spline̲surface.v̲closed:υ方向で曲面が閉じているかどうかの表示。これは,参考とする。
SELF\b̲spline̲surface.self̲intersect:曲面が自己干渉するかどうかを示すフラグ。これは,参考とする。
SELF\b̲spline̲surface.u̲upper:u方向での制御点の添字の上限。
SELF\b̲spline̲surface.v̲upper:υ方向での制御点の添字の上限。
SELF\b̲spline̲surface.control̲points:曲面の幾何を定義する制御点の(2次元)配列。この配列は,
control̲points̲listから作られる。
形式的要件
WR1:u方向のパラメタ化において矛盾が見いだせない場合,constraints̲param̲b̲splineは,TRUEを返す。
68
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WR2:υ方向のパラメタ化において矛盾が見いだせない場合,constraints̲param̲b̲splineは,TRUEを返す。
WR3:u̲multiplicitiesの個数は,u̲knotsの個数と同じとする。
WR4:v̲multiplicitiesの個数は,v̲knotsの個数と同じとする。
4.4.62 uniform̲surface これは,b̲spline̲surfaceの特殊な下位型とし,ノットが等間隔に配置されたも
のとする。この場合,ノット及びノット多重度に対して適切な暗黙値が導出される。
B-スプラインが一様であるとは,すべてのノット多重度が1で,すべてのノットが直前のノットとある
正の定数だけ異なることをいう。この下位型では,ノットは,−dから始まり,間隔は1.0とする。ここで,
dは次数とする。
EXPRESSによる定義
*)
ENTITY uniform̲surface
SUBTYPE OF (b̲spline̲surface);
END̲ENTITY;
(*
備考 曲面について明示的なノット値が要求されるときは,次のとおり導出される。
ku̲up=SELF\b̲spline̲surface.u̲upper+SELF\b̲spline̲surface.u̲degree+2
kv̲up=SELF\b̲spline̲surface.v̲upper+SELF\b̲spline̲surface.v̲degree+2
値ku̲upは,u方向におけるノット及びノット多重度のリストの添字の上限に必要なこ
とがある。これは,この方向における次数及び制御点の個数から計算される。
値kv̲upは,υ方向におけるノット及びノット多重度のリストの添字の上限に必要なこ
とがある。これは,この方向における次数及び制御点の個数から計算される。
u及びυの方向におけるノット多重度及びノットは,次の関数呼び出しによって計算する
ことができる。
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.u̲degree, ku̲up, uniform̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.u̲degree, ku̲up, uniform̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.v̲degree, kv̲up, uniform̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.v̲degree, kv̲up, uniform̲knots)
4.4.63 quasi̲uniform̲surface これは,b̲spline̲surfaceの特殊な下位型とし,最初のもの及び最後のもの
を除き,ノットは,等間隔に配置され,多重度1をもつ。この場合,ノット及びノット多重度に対して,
適切な暗黙値が導出される。
B-スプラインが準一様であるとは,ノットが端点では多重度 (degree+1) を,それ以外では多重度1をも
ち,各ノットが直前のノットからある正の定数だけ異なることをいう。この下位型では,ノットは,0.0
から始まり,その間隔は1.0とする。
EXPRESSによる定義
*)
ENTITY quasi̲uniform̲surface
SUBTYPE OF (b̲spline̲surface);
END̲ENTITY;
(*
備考 曲面について明示的なノット値が要求されるときは,次のとおり導出される。
69
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ku̲up=SELF\b̲spline̲surface.u̲upper-SELF\b̲spline̲surface.u̲degree+2
kv̲up=SELF\b̲spline̲surface.v̲upper-SELF\b̲spline̲surface.v̲degree+2
値ku̲upは,u方向におけるノット及びノット多重度のリストの添字の上限に必要なこ
とがある。これは,この方向における次数及び制御点の個数から計算される。
値kv̲upは,υ方向におけるノット及びノット多重度のリストの添字の上限に必要なこ
とがある。これは,この方向における次数及び制御点の個数から計算される。
u及びυの方向におけるノット多重度及びノットは,次の関数呼び出しによって計算する
ことができる。
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.u̲degree, ku̲up, quasi̲uniform̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.u̲degree, ku̲up, quasi̲uniform̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.v̲degree, kv̲up, quasi̲uniform̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.v̲degree, kv̲up, quasi̲uniform̲knots)
4.4.64 bezier̲surface これは,b̲spline̲surfaceの特殊な下位型とし,ノットが等間隔で,高い多重度を
もつものとする。この場合,ノット及びノット多重度に対して,適切な暗黙値が導出される。この下位型
では,ノットは0.0から始まり,その間隔は1.0とする。
EXPRESSによる定義
*)
ENTITY bezier̲surface
SUBTYPE OF (b̲spline̲surface);
END̲ENTITY;
(*
備考 曲面について明示的なノット値が要求されるときは,次のとおり導出される。
1
e.v̲degree
ine̲surfac
SELF/b̲spl
e.v̲upper
ine̲surfac
SELF/b̲spl
=
ku̲vp
+1
e.u̲degree
ine̲surfac
SELF/b̲spl
e.u̲upper
ine̲surfac
SELF/b̲spl
ku̲up=
+
値ku̲upは,u方向におけるノット及びその多重度のリストの添字の上限に必要なこと
がある。これは,この方向における次数及び制御点の個数によって計算される。
値kv̲upは,υ方向におけるノット及びその多重度のリストの添字の上限に必要なこと
がある。これは,この方向における次数及び制御点の個数によって計算される。
u及びυの方向におけるノット多重度及びノットは,次の関数呼び出しによって計算する
ことができる。
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.u̲degree, ku̲up, bezier̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.u̲degree, ku̲up, bezier̲knots)
default̲b̲spline̲knot̲mult(SELF\b̲spline̲surface.v̲degree, kv̲up, bezier̲knots)
default̲b̲spline̲knots(SELF\b̲spline̲surface.v̲degree, kv̲up, bezier̲knots)
4.4.65 rational̲b̲spline̲surface rational̲b̲spline̲surfaceは,制御点,関連付けられた重み及び基底関数
によって記述された区分的パラメタ有理曲面とする。この下位型は,b̲spline̲surfaceの他の下位型の一つ
(これは,基底関数を定義するためのノットの値を,明示的に又は暗黙に与える。)とともにインスタンス
化される。
70
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
曲面は,次のとおり解釈される。
∑∑
∑∑
1
0
2
0
2
1
1
0
2
0
2
1
)
(
)
(
)
(
)
(
)
,
(
K
i
K
j
dj
di
ij
K
i
K
j
dj
di
ij
ij
v
N
u
N
w
v
N
u
N
w
v
u
=
=
=
=
=
P
σ
備考 上の式で使用される記号については,4.4.60参照。
EXPRESSによる定義
*)
ENTITY rational̲b̲spline̲surface
SUBTYPE OF (b̲spline̲surface);
weights̲data : LIST [2:?]OF
LIST [2:?]OF REAL;
DERIVE
weights : ARRAY [0:u̲upper]OF
ARRAY [0:v̲upper]OF REAL
:= make̲array̲of̲array(weights̲data,0,u̲upper,0,v̲upper);
WHERE
WR1: (SIZEOF(weights̲data) =
SIZEOF(SELF\b̲spline̲surface.control̲points̲list))
AND (SIZEOF(weights̲data[1]) =
SIZEOF(SELF\b̲spline̲surface.control̲points̲list[1]));
WR2: surface̲weights̲positive(SELF);
END̲ENTITY;
(*
属性定義
weights̲data:有理のとき,制御点に関連付けられた重み。
weights:weights̲dataから構成される重みの(2次元)配列。
形式的要件
WR1:重みの配列の大きさは,制御点のデータと整合しなければならない。
WR2:個々の制御点に関連付けられた重みは,0.0を超えなければならない。
4.4.66 rectangular̲trimmed̲surface rectangular̲trimmed̲surfaceは,u=u1,u=u2,υ=υ1,及びυ=υ1という
等パラメタ線を境界とする単純なbounded̲surfaceとする。これらのすべての値は,参照された曲面のパラ
メタ範囲内でなければならない。パラメタ範囲の循環的な性質が仮定されている。
備考1. 例えば,三角関数(sin, cos)を用いて定義されるパラメタ形式をもつ曲面では,370°は,
10°と等価になる。rectangular̲trimmed̲surfaceは,パラメタ化をbasis̲surfaceから直接
継承しており,0から|u2−u1|まで及び0から|υ2−υ1|までのパラメタ範囲をもつ。前のパラ
メタから新しいパラメタを導出するには,4.4.34のアルゴリズムを用いる。
2. 曲面が与えられたパラメタ方向で閉じているときには,u2又はυ2の値がパラメタ範囲の
分だけ増えることを要求してもよい。
EXPRESSによる定義
*)
71
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ENTITY rectangular̲trimmed̲surface
SUBTYPE OF (bounded̲surface);
basis̲surface : surface;
u1 : parameter̲value;
u2 : parameter̲value;
v1 : parameter̲value;
v2 : parameter̲value;
usense : BOOLEAN;
vsense : BOOLEAN;
WHERE
WR1: u1 <> u2;
WR2: v1 <> v2;
WR3: (('GEOMETRY̲SCHEMA.ELEMENTARY̲SURFACE' IN TYPEOF(basis̲surface)) AND
(NOT('GEOMETRY̲SCHEMA.PLANE' IN TYPEOF(basis̲surface)))) OR
('GEOMETRY̲SCHEMA.SURFACE̲OF̲REVOLUTION' IN TYPEOF(basis̲surface)) OR
(usense =(u2 > u1));
WR4: (('GEOMETRY̲SCHEMA.SPHERICAL̲SURFACE' IN TYPEOF(basis̲surface)) OR
('GEOMETRY̲SCHEMA.TOROIDAL̲SURFACE' IN TYPEOF(basis̲surface))) OR
(vsense = (v2 > v1));
END̲ENTITY;
(*
属性定義
basis̲surface:トリムされる曲面。
u1:パラメタuの1番目の値。
u2:パラメタuの2番目の値。
v1:パラメタυの1番目の値。
v2:パラメタυの2番目の値。
usense:rectangular̲trimmed̲surfaceのパラメタuの方向が,basis̲surfaceのuの向きと同じか又は反対かを
指示するフラグ。
vsense:rectangular̲trimmed̲surfaceのパラメタυの方向が,basis̲surfaceのυの向きと同じか又は反対かを指
示するフラグ。
形式的要件
WR1:u1及びu2は,異なる値をもたなければならない。
WR2:v1及びv2は,異なる値をもたなければならない。
WR3:u方向で閉じている曲面を除いて,u̲senseは,uの順序付けられたパラメタ値と両立しなければな
らない。
WR4:υ方向で閉じている曲面を除いて,v̲senseは,υの順序付けられたパラメタ値と両立しなければな
らない。
非形式的要件
IP1:rectangular̲trimmed̲surfaceの定義域は,トリムされる元の曲面の定義域内になければならない。
72
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.67 curve̲bounded̲surface curve̲bounded̲surfaceは,1個以上のboundary̲curveによって定義される
boundaryをもつパラメタ曲面とする。これらの境界のうちの1個は,外周の境界でもよい。内部の境界の
個数は,幾つでもよい。外周の境界は,曲面の自然な境界として暗黙に定義されてもよい。このことは,
フラグimplicit̲outerがTRUEとなることによって示される。このとき,少なくとも1個の内部の境界が定
義されなければならない。(円柱のような)閉じた曲面のときは,与えられたどの境界が外周であるかを判
別できなくてもよい。basis̲surface上のcurve̲bounded̲surfaceの領域は,境界の任意の点からN×Tの方
向にあるbasis̲surfaceの部分として定義される。ここで,Nは曲面の法線とし,Tは境界の接ベクトルと
する。このようにして定義される領域は,弧状連結でなければならない。
EXPRIESSによる定義
*)
ENTITY curve̲bounded̲surface
SUBTYPE OF (bounded̲surface);
basis̲surface
: surface;
boundaries : SET[1:?]OF boundary̲curve;
implicit̲outer
: BOOLEAN;
WHERE
WR1: NOT(implicit̲outer AND
('GEOMETRY̲SCHEMA.OUTER̲BOUNDARY̲CURVE' IN TYPEOF(boundaries)));
WR2: (NOT(implicit̲outer)) OR
('GEOMETRY̲SCHEMA.BOUNDED̲SURFACE' IN TYPEOF(basis̲surface));
WR3: SIZEOF(QUERY(temp <* boundaries |
'GEOMETRY̲SCHEMA.OUTER̲BOUNDARY̲CURVE' IN
TYPEOF(temp))) <= 1;
WR4: SIZEOF(QUERY(temp <* boundaries |
(temp\composite̲curve̲on̲surface.basis̲surface[1]:<>:
SELF.basis̲surface))) = 0;
END̲ENTITY;
(*
属性定義
basis̲surface:境界付けられる曲面。
boundaries:曲面の境界曲線。ただし,暗黙の外周の境界が存在する場合は,それを除く。これらのうち,
outer̲boundary̲curveとすることで外周の境界として識別できるのは,たかだか1個とする。
implicit̲outer:TRUEのとき,曲面の自然な境界が外周の境界として用いられることを示すブール型のフ
ラグ。
備考 これらの属性の解釈は,図10参照。
形式的要件
WR1:implicit̲outerがTRUEのときは,明示的な外周の境界は,存在してはならない。
WR2:basis̲surfaceが境界付けられているときは,外周の境界は,暗黙にだけ定義されるものとする。
WR3:boundariesに含まれるouter̲boundary̲curveは,たかだか1個とする。
WR4:各boundary̲curveは,basis̲surface上になければならない。このことは,boundariesの各要素につい
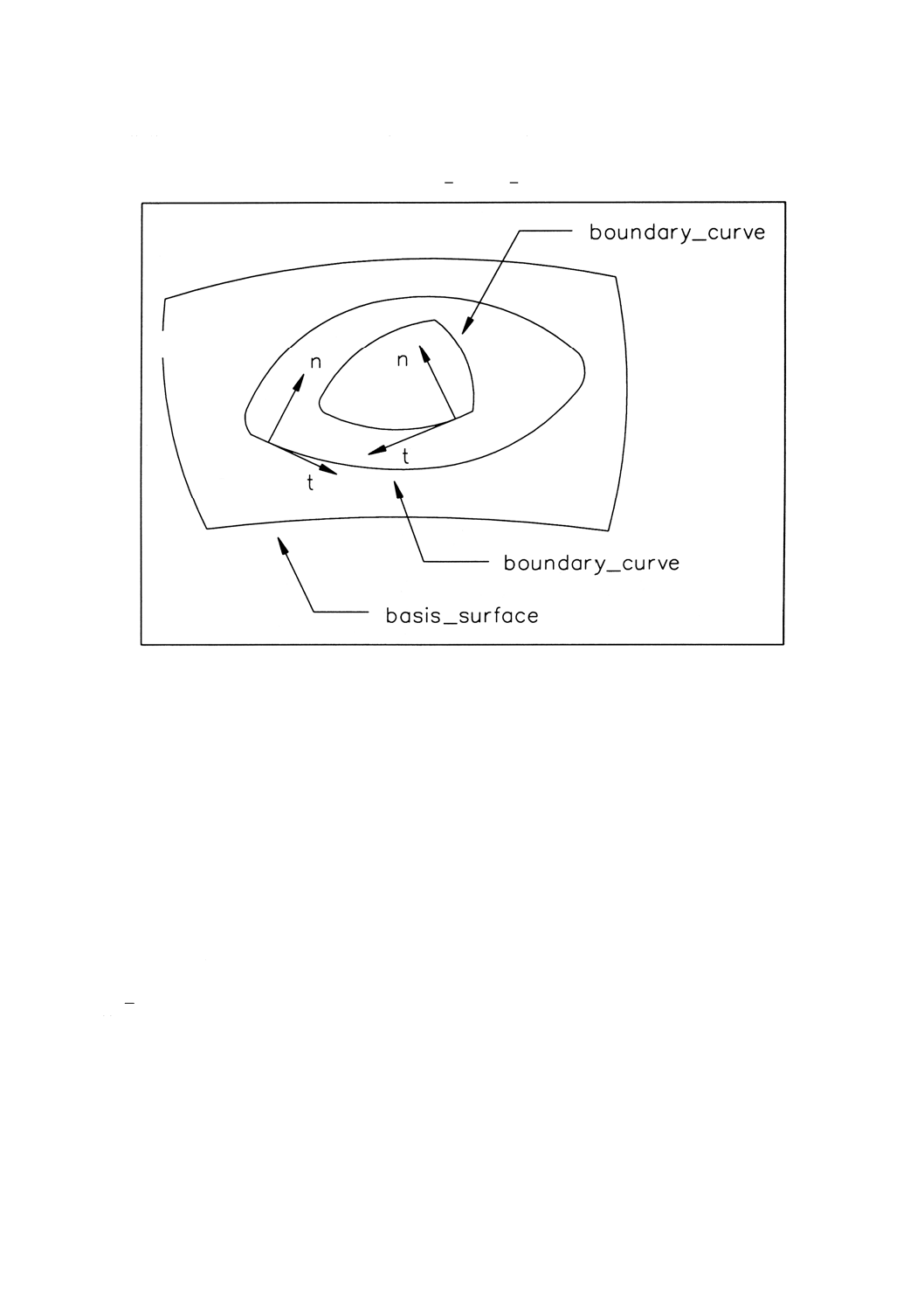
73
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
て上位型composite̲curve̲on̲surfaceの属性basis̲surfaceから確かめられる。
図10 curve̲bounded̲surface
非形式的要件
IP1:集合boundaries内の各曲線は,閉じていなければならない。
IP2:集合boundaries内のいかなる2本の曲線も,交差してはならない。
IP3:たかだか1個のboundary̲curveが他のすべてのboundary̲curveを囲んでもよい。outer̲boundary̲curve
が指定されたときは,その曲線だけが他のいかなるboundary̲curveをも囲む。
4.4.68 boundary̲curve boundary̲curveは,曲面の境界の定義に適したbounded̲curveの下位型とする。
EXPRESSによる定義
*)
ENTITY boundary̲curve
SUBTYPE OF (composite̲curve̲on̲surface);
WHERE
WR1: SELF\composite̲curve.closed̲curve;
END̲ENTITY;
(*
形式的要件
WR1:上位型composite̲curveの誘導属性closed̲curveは,TRUEでなければならない。
4.4.69 outer̲boundary̲curve これは,曲面の外周の境界を定義するという意味をもたせた
boundary̲curveの特殊な下位型とする。このような曲線は,curve̲bounded̲surfaceの集合boundaries内に2
個以上含まれてはならない。
74
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
ENTITY outer̲boundary̲curve
SUBTYPE OF (boundary̲curve);
END̲ENTITY;
(*
4.4.70 rectangular̲composite̲surface これは,n̲u×n̲v個のセグメント,すなわち,パッチの長方形配
列から構成される複合曲面とする。各セグメントは,有限で位相的に長方形とする(すなわち,各セグメ
ントがパラメタ空間内の長方形に対応する。)。セグメントは,b̲spline̲surfaceかrectangular̲trimmed̲surface
かのいずれかでなければならない。隣接するセグメント間では,u及びυの方向について,少なくとも位置
の連続性がなければならない。この複合曲面は,それぞれの方向について開いていても閉じていてもよい。
個々のセグメントSij(=segments[i][j])に関して,次が成り立つ。
− u方向の1個手前のセグメントをS(i-1)j,υ方向の1個手前のセグメントをSi(j-1)とする。1個後のセ
グメントも同様に,それぞれS(i+1)jとし,Si(j+1)とする。
− segments[i][j].u̲senseがTRUEのときは,SijがS(i+1)jと隣接する箇所の境界は,(基礎となる
bounded̲surfaceの)パラメタuの値が大きい方とする。segments[i][j].u̲senseがFALSEのときは,
この境界は,パラメタuの値が低い方とする。v̲senseについても同様とする。
− この複合曲面におけるSijのuに関するパラメタ化は,基礎となるbounded̲surfaceのパラメタ化
をi−1からiまで線形に写像したものとする。Uをrectangular̲composite̲surfaceのパラメタuと
し,uij(uij0≦uij≦uij1)をsegments[i][j]のパラメタuとするとき,これらのパラメタは,次の式に
よって関係付けられる。
segments[i][j].u̲sense=TRUEのとき,次のとおりとする。
U=(i−1)+
0
1
0
ij
ij
ij
ij
u
u
u
u
−
−
=uij0+(U−(i−1))(uij1−uij0)
segments[i][j].u̲sense=FALSEのとき,次のとおりとする。
U=i−
0
1
0
ij
ij
ij
ij
u
u
u
u
−
−
=uij0−(U−i)(uij1−uij0)
υに関するパラメタ化も同様にして得られる。したがって,複合曲面のパラメタ範囲は,0〜n̲u
及び0〜n̲vとなる。
− SijとS(i+1)jとの間での連続性は,segments[i][j].u̲transitionによって与えられる。
パッチS(n̲u)jについては,この複合曲面がu方向で開いているとき,discontinuousという値をと
ってもよい。それ以外のときは,曲面はここで閉じており,transition̲codeは,S1jへの連続性を示
す。v̲transitionについても同様とする。これらの場合を除いて,discontinuousは,surface̲patchの
transition̲codeに現れてはならない。
EXPRESSによる定義
*)
ENTITY rectangular̲composite̲surface
SUBTYPE OF (bounded̲surface);
segments : LIST [1:?]OF LIST [1:?]OF surface̲patch;
DERIVE
75
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
n̲u : INTEGER
:= SIZEOF(segments);
n̲v : INTEGER
:= SIZEOF(segments[1]);
WHERE
WR1: []= QUERY (s <* segments | n̲v <> SIZEOF (s));
WR2: constraints̲rectangular̲composite̲surface(SELF);
END̲ENTITY;
(*
属性定義
n̲u:u方向でのsurface̲patchの個数。
n̲v:υ方向でのsurface̲patchの個数。
segments:構成要素となるsurface̲patchの長方形配列(リストのリストによって表現される。)。各パッ
チは,向き及び遷移の情報をもつ。segments[i][j].u̲transitionは,segments[i][j]とsegments[i+1][j]との間の連
続性を示す。最後の列(segments[n̲u][j].u̲transition)は,曲面が(その行の)u方向で閉じていないこと
を示す値discontinuousをもってもよい。リストの残りの要素は,この値をもつことができない。最後の行
(segments[i][n̲v].v̲transition)は,曲面が(その列の)υ方向で閉じていないことを示す値discontinuous
をもってもよい。リストの残りの要素は,この値をもつことができない。
形式的要件
WR1:リストsegments内の各部分リストは,n̲v個のsurface̲patchをもたなければならない。
WR2:segmentsに関する制約は,次のとおりとする。
− 構成要素の曲面は,すべて,rectangular̲trimmed̲surface又はb̲spline̲surfaceとする。
− 最後の列又は行を除いて,リストsegments内のtransition̲codeは,discontinuousという値をもたな
い。値discontinuousが現れるときは,曲面がその方向で閉じていないことを示す。
非形式的要件
IP1:構成要素の曲面の向きは,segmentsの各要素のu̲sense及びv̲senseで指定される。
4.4.71 surface̲patch surface̲patchは,遷移及び向きの付加的な情報をもつbounded̲surfaceの下位型と
する。これは,rectangular̲composite̲surfaceを定義するのに用いる。
EXPRESSによる定義
*)
ENTITY surface̲patch
parent̲surface
: bounded̲surface;
u̲transition
: transition̲code;
v̲transition
: transition̲code;
u̲sense : BOOLEAN;
v̲sense : BOOLEAN;
INVERSE
using̲surfaces : BAG[1:?]OF rectangular̲composite̲surface FOR segments;
WHERE
WR1: (NOT ('GEOMETRY̲SCHEMA.CURVE̲BOUNDED̲SURFACE'
IN TYPEOF(parent̲surface)));
END̲ENTITY;
76
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(*
属性定義
parent̲surface:曲面の幾何及び境界を定義するsurface。
u̲transition:パッチの2番目のu境界が隣のパッチの1番目のu境界に接続するとき,この境界上で保証
される幾何的連続性。最後のパッチのとき,これは,rectangular̲composite̲surfaceの最初のu境界と最後
のu境界との連続性を定義する。
v̲transition:パッチの2番目のυ境界が隣のパッチの1番目のυ境界に接続するとき,この境界上で保証さ
れる幾何的連続性。最後のパッチのとき,これは,rectangular̲composite̲surfaceの最初のυ境界と最後のυ
境界との連続性を定義する。
u̲sense:これは,パッチの(パラメタ値が増加する)向きとparent̲surfaceの向きとの関係を定義する。
u̲senseがTRUEのとき,パッチの1番目のu境界は,パラメタuが最小値をとる境界となり,FALSEの
ときは,パラメタuが最大値をとる境界となる。
v̲sense:これは,パッチの(パラメタ値が増加する)向きとparent̲surfaceの向きとの関係を定義する。
v̲senseがTRUEのとき,パッチの1番目のυ境界は,パラメタυが最小値をとる境界となり,FALSEのと
きは,パラメタυが最大値をとる境界となる。
using̲surfaces:このsurface̲patchを定義に用いるrectangular̲composite̲surfaceの多重集合。この多重集合
は,空であってはならない。
形式的要件
WR1:curve̲bounded̲surfaceは,surface̲patchを定義するのに用いてはならない。
4.4.72 offset̲surface これは,元となる曲面から法線方向に一定の距離(distance)だけ離れている,単
純なオフセット曲面の手続き的な定義とする。distanceは,曲面のオフセットされる側を示し,正,負又
は0をとる。正の側と結果としてのオフセット曲面とは,次のとおり定義される。
(a) 元の曲面のu及びυの方向での単位接ベクトルを定義し,それぞれσu及びσυと表す。
(b) これらの外積N=σu×συをとる(σu及びσυは,線形独立でなければならない。さもなければオフセット
曲面は,存在しない。)。可能なときは,特異点においても,連続性によってNを定める。
(c) (曲面に対する)単位法線ベクトルを得るために,Nを正規化する。
(d) offset̲surface上の点を見つけるために,そのベクトルに沿ってオフセットする距離(0でもよい。)を
動く。
備考 この定義は,offset̲surfaceが自己干渉することを許す。
offset̲surfaceのパラメタ化は,basis̲surfaceのパラメタ化から直接得られる。すなわち,対応する点は,
同じパラメタ値をもつ。offset̲surfaceは,次のとおりパラメタ化される。
σ(u,v)=S(u,v)+dN
ここで,Nはパラメタ値 (u,υ) におけるbasis̲surface S (u,v) への単位法線ベクトルとし,dはdistanceと
する。
備考 このエンティティを使用するときには,オフセットする距離が,basis̲surfaceの任意の点
での曲率半径を超えないことが望ましい。特に曲面は,内部に尾根又は特異点をもたない
ことが望ましい。
EXPRESSによる定義
*)
ENTITY offset̲surface
77
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SUBTYPE OF (surface);
basis̲surface
: surface;
distance : length̲measure;
self̲intersect
: LOGICAL;
END̲ENTITY;
(*
属性定義
basis̲surface:オフセットされる曲面。
distance:オフセットする距離。正,負又は0をとる。距離は,曲面の法線の方向を正として測る。
self̲intersect:曲面が自己干渉するかどうかを示すフラグ。これは,参考とする。
4.4.73 surface̲replica これは,既に存在するsurfaceの複製(replica)を,異なる配置で定義する。これ
は,parent̲surface及び新たな位置を与えるtransformationを(場合によっては,拡大・縮小を含む。)参照
することで定義する。元となるsurfaceは,影響されない。生成されたsurfaceの幾何的な特徴は,
parent̲surfaceのものと同じとなる。しかし,transformationが拡大・縮小を含むときは,大きさが異なって
もよい。
EXPRESSによる定義
*)
ENTITY surface̲replica
SUBTYPE OF (surface);
parent̲surface : surface;
transformation : cartesian̲transformation̲operator̲3d;
WHERE
WR1: acyclic̲surface̲replica(SELF, parent̲surface);
END̲ENTITY;
(*
属性定義
parent̲surface :複製されるsurface。
transformation :parent̲surfaceに対するsurface̲replicaの配置,向き及び拡大・縮小を定義する
cartesian̲transformation̲operator̲3d。
形式的要件
WR1:surface̲replicaは,自分自身の定義に現れてはならない。
4.5
geometry̲schemaの規則定義
4.5.1
compatible̲dimension 規則compatible̲dimensionは,次のことを保証する。
(a) すべてのgeometric̲representation̲itemは,一つ以上のgeometric̲representation̲context座標空間に幾何
的に基礎付けられている。
(b) 複数のgeometric̲representation̲itemがともに一つの座標空間に幾何的に基礎付けられるとき,それら
は,それぞれか幾何的に基礎付けられている座標空間のdimension̲countと一対であることを保証する
ことによって,同一の座標空間のdimension̲countをもつ。
備考 一つのgeometric̲representation̲contextに幾何的に基礎付けられている2次元の
geometric̲representation̲item
は
,
coordinate̲space̲dimension
が
2
次
元
の
78
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
geometric̲representation̲contextに幾何的に基礎付けられるだけとする。このような関係にある
すべてのgeometric̲representation̲itemは,2次元とする。dimension̲countの他のすべての値は,
同様に振る舞う。
EXPRESSによる定義
*)
RULE compatible̲dimension FOR
(cartesian̲point,
direction,
representation̲context,
geometric̲representation̲context);
WHERE
-- 各々の cartesian̲point の coordinates の個数が,幾何的に基礎付けられ
-- ている geometric̲context のそれぞれの coordinate̲space̲dimension
-- に合致していることを保証する。
WR1: SIZEOF(QUERY(x <* cartesian̲point | SIZEOF(QUERY
(y <* geometric̲representation̲context | item̲in̲context(x,y) AND
(HIINDEX(x.coordinates) <> y.coordinate̲space̲dimension))) > 0 )) =0;
-- 各々の direction の direction̲ratios の個数が,幾何的に基礎付けられ
-- ている geometric̲context のそれぞれの coordinate̲space̲dimension
-- に合致していることを保証する。
WR2: SIZEOF(QUERY(x <* direction | SIZEOF(QUERY
(y <* geometric̲representation̲context | item̲in̲context(x,y) AND
(HIINDEX(x.direction̲ratios) <> y.coordinate̲space̲dimension)))
> 0 )) = 0;
END̲RULE;
(*
形式的要件
WR1:幾何的に基礎付けられているgeometric̲representation̲contextのcoordinate̲space̲dimensionの値と異
なる要素数のcoordinatesをもつcartesian̲pointは,存在しない。
WR2:幾何的に基礎付けられているgeometric̲representation̲contextのcoordinate̲space̲dimensionの値と異
なる要素数のdirection̲ratiosをもつdirectionは,存在しない。
備考 次の理由によって,cartesian̲point及びdirectionだけの検査は,すべての
geometric̲representation̲itemに対して十分とする。
(a) すべてのgeometric̲representation̲itemは,エンティティrepresentationの属性itemsか
ら伝わるrepresentation̲itemの木構造の中に表れる。JIS B 3700-43の中のエンティテ
ィrepresentation̲itemのWR1を参照。
(b) それぞれのgeometric̲representation̲itemは,その位置及び向きの情報を,この木構造
の中のcartesian̲point又はエンティティdirectionだけから得る。多くの場合,この参
照は,axis̲placementを経由してなされる。
(c) geometric̲representation̲itemは,座標空間との関連付け又はdimension̲countの割当て
79
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
以外の用途には,用いられない。
4.6
geometry̲schemaの関数定義 EXPRESS言語は,幾つかの組込み関数をもつ。ここでは,幾何スキ
ーマでの定義及び制約のために必要とされる付加的な関数に関して規定する。
4.6.1
dimension̲of 関数dimension̲ofは,入力geometric̲representation̲itemが幾何的に基礎付けられて
いるgeometric̲representation̲contextの整数dimension̲countを返す。
大域規則compatible̲dimensionにおける制約の効力によって,この値は,入力geometric̲representation̲item
のcoordinate̲space̲dimensionとする。この規則の定義は,4.5.1による。
EXPRESSによる定義
*)
FUNCTION dimension̲of(item : geometric̲representation̲item) :
dimension̲count;
LOCAL
x : SET OF representation;
y : representation̲context;
END̲LOCAL;
-- item が用いられている representation の集合を見つける。
x := using̲representations(item);
-- geometric̲representation̲context の dimension̲count を決定する。
-- context̲of̲items が geometric̲representation̲contextであり,
-- x のすべての値に対して同じ dimension̲count をもつことは,
-- 規則 compatible̲dimension によって保証されている。
y := x[1].context̲of̲items;
RETURN (y\geometric̲representation̲context.coordinate̲space̲dimension);
END̲FUNCTION;
(*
引数定義
item:(入力)dimension̲countを決定するgeometric̲representation̲item。
4.6.2
acyclic̲curve̲replica acyclic̲curve̲replicaブール関数は,与えられたcurve̲replicaが,それ自身
の定義に関与しているか否かを判定する再帰関数とする。関数は,curve̲replicaが,それ自身の定義にお
いて,直接的又は間接的にそれ自身を参照している場合,FALSEを返す。
EXPRESSによる定義
*)
FUNCTION acyclic̲curve̲replica(rep : curve̲replica; parent : curve)
: BOOLEAN;
IF NOT (('GEOMETRY̲SCHEMA.CURVE̲REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
END̲IF;
(* parent が,型 curve̲replica でない場合,TRUEを返す。*)
IF (parent :=: rep) THEN
RETURN (FALSE);
80
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(* parent が rep と同じ curve̲replica の場合,FALSEを返す。
それ以外の場合,parent の parent̲curve で再び関数を呼ぶ。*)
ELSE RETURN(acyclic̲curve̲replica(rep, parent\curve̲replica.parent̲curve));
END̲IF;
END̲FUNCTION;
(*
引数定義
rep:(入力)循環的参照を検査するcurve̲replica。
parent:(入力)curve̲replicaの定義の中で使われるcurve。
4.6.3
acyclic̲point̲replica acyclic̲point̲replicaブール関数は,与えられたpoint̲replicaが,それ自身の
定義に関与しているか否かを判定する再帰関数とする。関数は,point̲replicaが,それ自身の定義におい
て,直接的又は間接的にそれ自身を参照している場合,FALSEを返す。
EXPRESSによる定義
*)
FUNCTION acyclic̲point̲replica(rep : point̲replica; parent : point)
: BOOLEAN;
IF NOT (('GEOMETRY̲SCHEMA.POINT̲REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
END̲IF;
(* parent が,型 point̲replica でない場合,TRUE を返す。*)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* parent が rep と同じ point̲replica の場合,FALSE を返す。
それ以外の場合,parent の parent̲pt で再び関数を呼ぶ。*)
ELSE RETURN(acyclic̲point̲replica(rep, parent\point̲replica.parent̲pt));
END̲IF;
END̲FUNCTION;
(*
引数定義
rep:(入力)循環的参照を検査するpoint̲replica。
parent:(入力)point̲replicaの定義の中で使われるpoint。
4.6.4
acyclic̲surface̲replica acyclic̲surface̲replicaブール関数は,与えられたsurface̲replicaか,それ
自身の定義に関与しているか否かを判定する再帰関数とする。関数は,surface̲replicaが,それ自身の定義
において,直接的又は間接的にそれ自身を参照している場合,FALSEを返す。
EXPRESSによる定義
*)
FUNCTION acyclic̲surface̲replica(rep : surface̲replica; parent : surface)
: BOOLEAN;
IF NOT (('GEOMETRY̲SCHEMA.SURFACE̲REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
81
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲IF;
(* parent が,型 surface̲replica でない場合,TRUE を返す。*)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* parentが,rep と同じ surface̲replica である場合,FALSE を返す。
それ以外の場合,parent の parent̲surface で再び関数を呼ぶ。*)
ELSE RETURN(acyclic̲surface̲replica(rep, parent\
surface̲replica.parent̲surface));
END̲IF;
END̲FUNCTION;
(*
引数定義
rep:(入力)循環的参照を検査するsurface̲replica。
parent:(入力)surface̲replicaの定義の中で使われるsurface。
4.6.5
associated̲surface この関数は,pcurve̲or̲surfaceに関係付けられている唯一の曲面を決定する。
この関数は,surface̲curve及びその下位型に対する制約に必要となる。
EXPRESSによる定義
*)
FUNCTION associated̲surface(arg : pcurve̲or̲surface) : surface;
LOCAL
surf : surface;
END̲LOCAL;
IF 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(arg) THEN
surf := arg.basis̲surface;
ELSE
surf := arg;
END̲IF;
RETURN(surf);
END̲FUNCTION;
(*
引数定義
arg:(入力)関係付けられたparent̲surfaceを決定する必要のあるpcurve̲or̲surface。
surf:(出力)argと関係付けられるparent̲surface。
4.6.6 base̲axis この関数は,3個の正規化された直交するdirection u[1],u[2]及びu[3]を返す。3次元の
場合には,完全な入力データに対して,u[3]はaxis3の方向,u[1]はaxis1をu[3]に垂直な平面に投影した方
向,u[2]はu[1]及びu[3]の双方に直交しaxis2と同じ向きの方向とする。2次元の場合には,u[1]はaxis1の
方向とし,u[2]はu[1]に垂直でaxis2と同じ向きの方向とする。不完全な入力データの場合は,暗黙値が導
入される。
EXPR:ESSによる定義
*)
82
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
FUNCTION base̲axis(dim : INTEGER; axis1, axis2, axis3 : direction):
LIST [2:3] OF direction;
LOCAL
vec : direction;
u
: LIST [2:3] OF direction;
factor : REAL;
END̲LOCAL;
IF (dim =3) THEN
u[3] := NVL(normalise(axis3), direction([0.0,0.0,1.0]));
u[1] := first̲proj̲axis(u[3],axis1);
u[2] := second̲proj̲axis(u[3],u[1],axis2);
ELSE
u[3] := ?;
IF EXISTS(axis1) THEN
u[1] := normalise(axis1);
u[2] := orthogonal̲complement(u[1]);
IF EXISTS(axis2) THEN
factor := dot̲product(axis2,u[2]);
IF (factor < 0.0) THEN
u[2].direction̲ratios[1] := -u[2].direction̲ratios[1];
u[2].direction̲ratios[2] := -u[2].direction̲ratios[2];
END̲IF;
END̲IF;
ELSE
IF EXISTS(axis2) THEN
u[2] := normalise(axis2);
u[1] := orthogonal̲complement(u[2]);
u[1].direction̲ratios[1] := -u[1].direction̲ratios[1];
u[1].direction̲ratios[2] := -u[1].direction̲ratios[2];
ELSE
u[1].direction̲ratios[1] := 1.0;
u[1].direction̲ratios[2] := 0.0;
u[2].direction̲ratios[1] := 0.0;
u[2].direction̲ratios[2] := 1.0;
END̲IF;
END̲IF;
END̲IF;
RETURN(u);
END̲FUNCTION;
(*
83
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
引数定義
dim:(入力)正規化された直交する方向を必要とする空間の次元の整数値。
axis1:(入力)出力軸u[1]の方向の最初の近似として用いるdirection。
axis2:(入力)u[2]の向きを決定するのに用いるdirection。
axis3:(入力)dim=3の場合はu[3]の方向,dim=2の場合は不定“?”。
u:(出力)互いに直交するdim個(すなわち,2個又は3個)の方向のリスト。
参考 不定“?”は,原国際規格では“NULL”と表記されている。EXPRESSにおいて,“NULL”は
予約語ではないが,“?”は集合やリストの不定上限を示す記号であることから,原国際規格の
表現は“?”を表すものと解釈できる。この規格では,JIS B 3700-11の表記法に従い,不定“?”
と表記した。
4.6.7
build̲2axes この関数は,正規化された2個の直交するdirectionを返す。u[1]はref̲directionの方
向とし,u[2]はu[1]に垂直とする。入力データが不完全な場合には,ref̲directionの暗黙値として,(1.0, 0.0)
が与えられる。
EXPRESSによる定義
*)
FUNCTION build̲2axes(ref̲direction : direction) : LIST [2:2] OF direction;
LOCAL
u : LIST [2:2] OF direction;
END̲LOCAL;
u[1] := NVL(normalise(ref̲direction), direction([1.0,0.0]));
u[2] := orthogonal̲complement(u[1]);
RETURN(u);
END̲FUNCTION;
(*
引数定義
ref̲direction:(入力)2次元空間における参照direction。暗黙値は,(1.0,0.0)とする。
u:(出力)2個の互いに直交するdirectionのリストで,u[1]は,ref̲directionに平行とする。
4.6.8 build̲axes この関数は,正規化された3個の直交するdirectionを返す。u[3]はaxisの方向とし,u[1]
はref̲directionをu[3]に垂直な平面に投影した方向,u[2]はu[3]とu[1]との外積とする。入力データが不完
全な場合には,暗黙値が与えられる。
EXPRESSによる定義
*)
FUNCTION build̲axes(axis, ref̲direction : direction):
LIST [3:3] OF direction;
LOCAL
u : LIST[3:3] OF direction;
END̲LOCAL;
u[3] := NVL(normalise(axis), direction([0.0,0.0,1.0]));
u[1] := first̲proj̲axis(u[3], ref̲direction);
u[2] := normalise(cross-product(u[3], u[1])).orientation;
84
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
RETURN(u);
END̲FUNCTION;
(*
引数定義
axis:(入力)u[3]のdirection。暗黙値は,(0.0, 0.0, 1.0)とする。
ref̲direction:(入力)u[1]を計算するのに用いるdirection。
u:(出力)3次元空間における3個の互いに直交するdirectionのリストとする。
4.6.9
orthogonal̲complement この関数は,入力されたdirectionに対して直交補空間のdirectionを返す。
入力は2次元のdirectionとし,結果は入力に対して垂直なdirectionとする。
EXPRESSによる定義
*)
FUNCTION orthogonal̲complement(vec : direction) : direction;
LOCAL
result : direction;
END̲LOCAL;
IF (vec.dim <> 2) OR NOT EXISTS (vec) THEN
RETURN(?);
ELSE
result.direction̲ratios[1] := -vec.direction̲ratios[2];
result.direction̲ratios[2] := vec.direction̲ratios[1];
RETURN(result);
END̲IF;
END̲FUNCTION;
(*
引数定義
vec:(入力)2次元空間内のdirection。
result:(出力)vecに直交するdirection。
4.6.10 first̲proj̲axis この関数は,入力データが完全な場合,argをz̲axisに垂直な平面に投影した3次
元のdirectionを生成する。argは,暗黙値をもち,その場合,(1,0,0)を平面に投影した結果が得られる。
ただし,z̲axisが(1,0,0)の場合には,argの暗黙値として(0,1,0)が用いられる。argが入力されたz̲axis
と同じ方向の場合には,戻り値を不定“?”とする。
EXPRESSによる定義
*)
FUNCTION first̲proj̲axis(z̲axis, arg : direction) : direction;
LOCAL
x̲axis : direction;
v : direction;
z : direction;
x̲vec : vector;
END̲LOCAL;
85
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF (NOT EXISTS(z̲axis)) OR (NOT EXISTS(arg)) OR (arg.dim <> 3) THEN
x̲axis := ?;
ELSE
z̲axis := normalise(z̲axis);
IF NOT EXISTS(arg) THEN
IF (z̲axis <> direction([1.0,0.0,0.0])) THEN
v := direction([1.0,0.0,0.0]);
ELSE
v := direction([0.0,1.0,0.0]);
END̲IF;
ELSE
IF ((cross̲product(arg,z).magnitude) =0.0) THEN
RETUR (?);
ELSE
V := normalise(arg);
END̲IF;
END̲IF;
x̲vec := scalar̲times̲vector(dot̲product(v, z), z̲axis);
x̲axis := vector̲difference(v, x̲vec).orientation;
x̲axis := normalise(x̲axis);
END̲IF;
RETURN(x̲axis);
END̲FUNCTION;
(*
引数定義
z̲axis:(入力)局所Z軸を定義するdirection。
arg:(入力)z̲axisに平行でないdirection。
x̲axis:(出力)法線がz̲axisである平面上へのargの投影の方向にあるdirection。
4.6.11 second̲proj̲axis この関数は,argをz̲axisに垂直な平面に投影し,更にx̲axisに垂直な平面に投
影した正規化されたベクトルを返す。argが不定“?”の場合には,ベクトル(0,1,0)をz̲axisに投影した
ものが返される。
EXPRESSによる定義
*)
FUNCTION second̲proj̲axis(z̲axis, x̲axis, arg: direction) : direction;
LOCAL
y̲axis : vector;
v
: direction;
temp : vector;
END̲LOCAL;
IF NOT EXISTS(arg) THEN
86
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
v := direction([0.0,1.0,0.0]);
ELSE
v := arg;
END̲IF;
temp := scalar̲times̲vector(dot̲product(v, z̲axis), z̲axis);
y̲axis
:= vector̲difference(v, temp);
temp := scalar̲times̲vector(dot̲product(v, x̲axis), x̲axis);
y̲axis
:= vector̲difference(y̲axis, temp);
y̲axis
:= normalise(y̲axis);
RETURN(y̲axis.orientation);
END̲FUNCTION;
(*
引数定義
z̲axis:(入力)局所Z軸を定義するdirection。
x̲axis:(入力)z̲axisに平行でないdirection。
arg:(入力)y̲axisの最初の近似として用いられるdirection。
y̲axis.orientation:(出力)まずargをz̲axisを法線としてもつ平面上に投影し,その結果をx̲axisを法線
としてもつ平面上に投影することで決定されるdirection。
4.6.12 cross̲product この関数は,入力された2個のdirectionのベクトル積,すなわち,外積を返す。3
次元のdirectionが入力され,かつ計算開始のときに正規化される。結果は,常に単位をもたないvectorと
する。入力された2個のdirectionが平行又は逆向きに平行の場合には,orientationかarg1に等しく,magnitude
が0のvectorが返される。
EXPRESSによる定義
*)
FUNCTION cross̲product(arg1, arg2 : direction) : vector;
LOCAL
mag : REAL;
res : direction;
v1,v2 : LIST [3:3] OF REAL;
result : vector;
END̲LOCAL;
IF (NOT EXISTS (arg1) OR (arg1.dim = 2)) OR
(NOT EXISTS (arg2) OR (arg2.dim = 2)) THEN
RETURN(?);
ELSE
BEGIN
v1 := normalise(arg1).direction̲ratios;
v2 := normalise(arg2).direction̲ratios;
res.direction̲ratios[1] := (v1[2]*v2[3] - v1[3]*v2[2]);
res.direction̲ratios[2] := (v1[3]*v2[1] - v1[1]*v2[3]);
87
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
res.direction̲ratios[3] := (v1[1]*v2[2] - v1[2]*v2[1]);
mag := 0.0;
REPEAT i := 1 T0 3;
mag := mag + res.direction̲ratios[i]*res.direction̲ratios[i];
END̲REPEAT;
IF (mag > 0.0) THEN
result.orientation := res;
result.magnitude := SQRT(mag);
ELSE
result.orientation := arg1;
result.magnitude := 0.0;
END̲IF;
RETURN(result);
END;
END̲IF;
END̲FUNCTION;
(*
引数定義
arg1:(入力)外積演算における第1の演算項を定義するdirection。
arg2:(入力)外積演算における第2の演算項を定義するdirection。
result:(出力)arg1とarg2との外積を表すvector。
4.6.13 dot̲product この関数は,入力された2個のdirectionのスカラ積,すなわち,内積を返す。2次元
又は3次元のdirectionが入力され,かつ計算開始のときに正規化される。入力された2個のdirectionが異
なる次元数をもつ場合,又はいずれか一方が未定義の場合には,返されるスカラは,不定“?”とする。
EXPRESSによる定義
*)
FUNCTION dot̲product(arg1, arg2 : direction) : REAL;
LOCAL
scalar : REAL;
vec1, vec2 : direction;
ndim : INTEGER;
END̲LOCAL;
IF NOT EXISTS (arg1) OR NOT EXISTS (arg2) THEN
scalar := ?;
(* 関数が不適切なデータで呼ばれた場合には,
結果として不定“?”が返される。*)
ELSE
IF (arg1.dim <> arg2.dim) THEN
scalar := ?;
(* 関数が不適切なデータで呼ばれた場合には,
88
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
結果として不定“?”が返される。*)
ELSE
BEGIN
vec1 := normalise(arg1);
vec2 := normalise(arg2);
ndim := arg1.dim;
scalar := 0.0;
REPEAT i
:= 1 TO ndim;
scalar
:= scalar +
vec1.direction̲ratios[i]*vec2.direction̲ratios[i];
END̲REPEAT;
END;
END̲IF;
END̲IF;
RETURN(scalar);
END̲FUNCTION;
(*
引数定義
arg1:(入力)内積,すなわち,スカラ積演算における第1のvectorを定義するdirection。
arg2:(入力)内積,すなわち,スカラ積演算における第2のvectorを定義するdirection。
scalar:(出力)arg1とarg2との内積を表すスカラ。
4.6.14 normalise この関数は,正規化して成分の2乗和を1.0としたvector又はdirectionを返す。出力は,
入力引数と同じ型(同じ単位をもつ,direction又はvector)とする。入力引数が未定義又は長さが0の場
合には,出力vectorは,不定“?”とする。
EXPRESSによる定義
*)
FUNCTION normalise(arg : vector̲or̲direction) : vector̲or̲direction;
LOCAL
ndim : INTEGER;
v
: direction;
result : vector̲or̲direction;
vec : vector;
mag : REAL;
END̲LOCAL;
IF NOT EXISTS(arg) THEN
result := ?;
(* 関数が不適切なデータで呼ばれた場合には,
結果として不定“?”が返される。*)
ELSE
ndim := arg.dim;
89
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg) THEN
BEGIN
vec := arg;
v := arg.orientation;
IF arg.magnitude = 0.0 THEN
RETURN(?);
ELSE
vec.magnitude := 1.0;
END̲IF;
END;
ELSE
V := arg;
END̲IF;
mag := 0.0;
REPEAT i:=1 TO ndim;
mag := mag + v.direction̲ratios[i]*v.direction̲ratios[i];
END̲REPEAT;
IF mag > 0.0 THEN
mag := SQRT(mag);
REPEAT i := 1 TO ndim;
v.direction̲ratios[i] := v.direction̲ratios[i]/mag;
END̲REPEAT;
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg) THEN
Vec.orientation := v;
result := vec;
ELSE
result := v;
END̲IF;
ELSE
RETURN(?);
END̲IF;
END̲IF;
RETURN (result);
END̲FUNCTION;
(*
引数定義
arg:(入力)正規化するvector又はdirection。
result:(出力)argに平行で,長さが1のvector又はdirection。
90
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.6.15 scalar̲times̲vector この関数は,入力ベクトルをスカラ倍したベクトルを返す。これは,入力と
してスカラとdirection又はvectorとを受け取る。出力は,vectorとするが,入力がvectorの場合にはその
vectorと同じ単位をもち,入力がdirectionの場合には単位をもたない。入力引数が未定義の場合,返され
るvectorは不定“?”とする。スカラが負の場合には,vectorのorientationが反転する。
EXPRESSによる定義
*)
FUNCTION scalar̲times̲vector (scalar
: REAL; vec : vector̲or̲direction)
: vector;
LOCAL
v
: direction;
mag : REAL;
result : vector;
END̲LOCAL;
IF NOT EXISTS (scalar) OR NOT EXISTS (vec) THEN
result := ?;
(* 関数が不適切なデータで呼ばれた場合には,
結果として不定“?”が返される。*)
ELSE
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF (vec) THEN
v := vec.orientation;
mag
:= scalar * vec.magnitude;
ELSE
v
:= vec;
mag
:= scalar;
END̲IF;
IF (mag < 0.0 ) THEN
REPEAT i := 1 TO SIZEOF(v.direction̲ratios);
v.direction̲ratios[i] := -v.direction̲ratios[i];
END̲REPEAT;
mag := -mag;
END̲IF;
result.orientation := normalise(v);
result.magnitude := mag;
END̲IF;
RETURN (result);
END̲FUNCTION;
(*
引数定義
scalar:(入力)積演算に用いられる実数。
vec:(入力)スカラ倍されるvector̲or̲direction。
91
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
result:(出力)scalarとvecとの積を表すvector。
4.6.16 vector̲sum この関数は,入力引数の和を返す。これは,入力された2個のvector又はdirection
のベクトル和をvectorとして返す。ここでは,directionを単位ベクトルとして扱う。2個の入力引数は,
同じ次元数をもたなければならないが,direction又はvectorのいずれでもよい。両方の引数がvectorの場
合には,それらは同じ単位でなければならない。和が0のベクトルになるときは,orientationがarg1に等
しく,magnitudeが0のvectorを生成する。両方の入力引数がdirectionの場合には,結果は,単位をもた
ない。
EXPRESSによる定義
*)
FUNCTION vector̲sum(arg1, arg2 : vector̲or̲direction) : vector;
LOCAL
result
: vector;
res, vec1, vec2 : direction;
mag, mag1, mag2 :REAL;
ndim
: INTEGER;
END̲LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS (arg2))) OR (arg1.dim <> arg2.dim)
THEN
result := ?;
(* 関数が不適切なデータで呼ばれた場合には,
結果として不定“?”が返される。*)
ELSE
BEGIN
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
mag1 := arg1.magnitude;
vec1 := arg1.orientation;
ELSE
mag1 := 1.0;
vec1 := arg1;
END̲IF;
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2.magnitude;
vec2 := arg2.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
END̲IF;
vec1 := normalise(vec1);
vec2 := normalise(vec2);
ndim := SIZEOF(vec1.direction̲ratios);
92
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
mag := 0.0;
REPEAT i := 1 TO ndim;
res.direction̲ratios[i] := mag1*vec1.direction̲ratios[i] +
mag2*vec2.direction̲ratios[i];
mag := mag + (res.direction̲ratios[i]*res.direction̲ratios[i]);
END̲REPEAT;
IF (mag > 0.0) THEN
result.magnitude := SQRT(mag);
result.orientation := res;
ELSE
result.magnitude := 0.0;
result.orientation := vec1;
END̲IF;
END;
END̲IF;
RETURN (result);
END̲FUNCTION;
(*
引数定義
arg1:(入力)ベクトル和演算における第1の演算項を定義するdirection。
arg2:(入力)ベクトル和演算における第2の演算項を定義するdirection。
result:(出力)arg1とarg2とのベクトル和を表すvector。
4.6.17 vector̲difference この関数は,入力引数の差を(arg1−arg2)として返す。これは,入力された2
個のvector又はdirectionの差分ベクトルをvectorとして返す。ここでは,directionを単位ベクトルとして
扱う。2個の入力引数は,同じ次元数をもたなければならないが,direction又はvectorのいずれでもよい。
両方の引数がvectorの場合には,それらは同じ単位でなければならない。両方がdirectionの場合には,結
果は単位をもたない。差が0のベクトルになるときは,orientationがarg1に等しく,magnitudeが0のvector
を生成する。
EXPRESSによる定義
*)
FUNCTION vector̲difference(arg1, arg2 : vector̲or̲direction) : vector;
LOCAL
result : vector;
res, vec1, vec2 : direction;
mag, mag1, mag2 : REAL;
ndim
: INTEGER;
END̲LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS(arg2))) OR (arg1.dim <> arg2.dim)
THEN
result := ?;
93
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(* 関数が不適切なデータで呼ばれた場合には,
結果として不定“?”が返される。*)
ELSE
BEGIN
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
mag1 := arg1.magnitude;
vec1 := arg1.orientation;
ELSE
mag1 := 1.0;
vec1 := arg1;
END̲IF;
IF 'GEOMETRY̲SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2.magnitude;
vec2 := arg2.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
END̲IF;
vec1 := normalise (vec1);
vec2 := normalise (vec2);
ndim := SIZEOF(vec1.direction̲ratios);
mag := 0.0;
REPEAT i := 1 TO ndim;
res.direction̲ratios[i] := mag1*vec1.direction̲ratios[i]-
mag2*vec2.direction̲ratios[i];
mag := mag + (res.direction̲ratios[i]*res.direction̲ratios[i]);
END̲REPEAT;
IF (mag > 0.0 ) THEN
result.magnitude := SQRT(mag);
result.orientation := res;
ELSE
result.magnitude := 0.0;
result.orientation := vec1;
END̲IF;
END;
END̲IF;
RETURN (result);
END̲FUNCTION;
(*
引数定義
94
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
arg1:(入力)差分ベクトルの演算における第1の演算項を定義するdirection。
arg2:(入力)差分ベクトルの演算における第2の演算項を定義するdirection。
result:(出力)arg1とarg2との差分ベクトルを表すvector。
4.6.18 default̲b̲spline̲knot̲mult この関数は,B-スプラインのパラメタ化のための,ノット多重度の整
数リストを返す。ノット多重度は,knot̲typeに依存する。
EXPRESSによる定義
*)
FUNCTION default̲b̲spline̲knot̲mult(degree, up̲knots : INTEGER;
uniform
: knot̲type)
: LIST [2:?] OF INTEGER;
LOCAL
knot̲mult : LIST [1:up̲knots] OF INTEGER;
END̲LOCAL;
REPEAT i := 1 TO up̲knots;
knot̲mult[i] := 0;
END̲REPEAT;
IF uniform = uniform̲knots THEN
REPEAT i := 1 TO up̲knots;
knot̲mult[i] := 1;
END̲REPEAT;
END̲IF;
IF uniform = quasi̲uniform̲knots THEN
knot̲mult[1] := degree + 1;
knot̲mult[up̲knots] := degree + 1;
REPEAT i := 2 TO (up̲knots - 1);
knot̲mult[i] := 1;
END̲REPEAT;
END̲IF;
IF uniform = piecewise̲bezier̲knots THEN
knot̲mult[1] := degree + 1;
knot̲mult[up̲knots] := degree + 1;
REPEAT i := 2 TO (up̲knots-1);
knot̲mult[i] := degree;
END̲REPEAT;
END̲IF;
RETURN(knot̲mult);
END̲FUNCTION;
(*
引数定義
degree:(入力)B-スプライン基底関数の次数を定める整数。
95
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
up̲knots:(入力)求めるノット多重度の個数を与える整数。
uniform:(入力)ノット多重度の決定に必要な基底関数の型。
knot̲mult:(出力)ノット多重度の整数リスト。
4.6.19 default̲b̲spline̲knots この関数は,B-スプラインのパラメタ化のための,ノットベクトルを返す。
このノットベクトルは,knot̲typeに依存する。
EXPRESSによる定義
*)
FUNCTION default̲b̲spline̲knots(degree,up̲knots : INTEGER;
uniform
: knot̲type)
: LIST [2:?] OF parameter̲value;
LOCAL
knots : LIST[1:up̲knots] OF parameter̲value;
ishift : INTEGER := 1;
END̲LOCAL;
REPEAT i := 1 TO up̲knots;
knots[i] := 0;
END̲REPEAT;
IF (uniform = uniform̲knots) THEN
ishift := degree + 1;
END̲if;
IF (uniform = uniform̲knots) OR
(uniform = quasi̲uniform̲knots) OR
(uniform = piecewise-bezier-knots) THEN
REPEAT i := 1 TO up̲knots;
knots[i] := i - ishift;
END̲REPEAT;
END̲IF;
RETURN(knots);
END̲FUNCTION;
(*
引数定義
degree:(入力)B-スプライン基底関数の次数を定める整数。
up̲knots:(入力)求めるノット値の個数を与える整数。
uniform:(入力)knotsの決定に必要な基底関数の型。
knots:(出力)ノットのパラメタ値のリスト。
4.6.20 default̲b̲spline̲curve̲weights この関数は,大きさ1.0の重みをup̲cp個の実数型の配列に入れ
て返す。
EXPRESSによる定義
*)
FUNCTION default̲b̲spline̲curve̲weights(up̲cp : INTEGER)
96
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
: ARRAY [0:up̲cp] OF REAL;
LOCAL
weights : ARRAY [0:up̲cp] OF REAL;
END̲LOCAL;
REPEAT i := 0 TO up̲cp;
weights[i] := 1;
END̲REPEAT;
RETURN(weights);
END̲FUNCTION;
(*
引数定義
up̲cp:(入力)求めるB-スプライン曲線の重み配列の添字の上限。
weights:(出力)重みの実数配列。
備考 この関数は,この規格では用いないが,アプリケーションプロトコルで用いるために,こ
こで定義する。
4.6.21 default̲b̲spline̲surface̲weights この関数は,大きさ1.0の重みを2次元の実数型配列に入れて
返す。
EXPRESSによる定義
*)
FUNCTION default̲b̲spline̲surface̲weights(u̲upper, v̲upper: INTEGER)
: ARRAY [0:u̲upper] OF
ARRAY [0:v̲upper] OF REAL;
LOCAL
weights : ARRAY [0:u̲upper] OF ARRAY [0:v̲upper] OF REAL;
END̲LOCAL;
REPEAT i := 0 TO u̲upper;
REPEAT j := 0 TO v̲upper;
weights[i][j] := 1;
END̲REPEAT;
END̲REPEAT;
RETURN(weights);
END̲FUNCTION;
(*
引数定義
u̲upper:(入力)求めるB-スプライン曲面のu方向の重み配列の添字の上限。
v̲upper:(入力)求めるB-スプライン曲面のυ方向の重み配列の添字の上限。
weights:(出力)重みの2次元の実数配列。
備考 この関数は,この規格では用いないが,アプリケーションプロトコルで用いるために,こ
こで定義する。
97
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.6.22 constraints̲param̲b̲spline この関数は,b̲spline̲curve又はb̲spline̲surface(の一方向)のパラ
メタ化を調べ,次の制約をすべてみたす場合にTRUEを返す。
(a) 次数が1以上。
(b) ノットの添字の上限が2以上。
(c) 制御点の添字の上限が次数以上。
(d) ノット多重度の和=次数+制御点の添字の上限+2。
(e) 最初及び最後のノットの多重度は,1以上,かつ(次数+1)以下とする。
(f) 他のすべてのノットに関しては,ノットの多重度は,1以上,かつ次数以下とする。
(g) ノットの値は,単調に増加する。
EXPRESSによる定義
*)
FUNCTION constraints̲param̲b̲spline(degree, up̲knots, up̲cp : INTEGER;
knot̲mult : LIST OF INTEGER;
knots : LIST OF parameter̲value) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
k,l,sum : INTEGER;
END̲LOCAL;
(* ノット多重度の和を求める。*)
sum := knot̲mult[1];
REPEAT i := 2 TO up̲knots;
sum := sum + knot̲mult[i];
END̲REPEAT;
(* すべてのB-スプラインのパラメタ化についての制限を検査する。*)
IF (degree < 1) OR (up̲knots < 2) OR (up̲cp < degree) OR
(sum <> (degree + up̲cp + 2)) THEN
result := FALSE;
RETURN(result);
END̲IF;
k := knot̲mult[1];
IF (k < 1) OR (k > degree + 1) THEN
result := FALSE;
RETURN(result);
END̲IF;
REPEAT i := 2 TO up̲knots;
IF (knot̲mult[i] <1) OR (knots[i] <= knots[i-1]) THEN
result := FALSE;
RETURN(result);
END̲IF;
k := knot̲mult[i];
98
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF (i < up̲knots) AND (k > degree) THEN
result := FALSE;
RETURN(result);
END̲IF;
IF (i=up-knots) AND (k > degree + 1) THEN
result := FALSE;
RETURN(result);
END̲IF;
END̲REPEAT;
RETURN(result);
END̲FUNCTION;
(*
引数定義
degree:(入力)B-スプライン基底関数の次数を定める整数。
up̲knots:(入力)ノット多重度のリストの添字の上限を与える整数。
up̲cp:(入力)パラメタ値の整合性を検査する曲線又は曲面の制御点の添字の上限を与える整数。
knot̲mult:(入力)ノット多重度のリスト。
4.6.23 curve̲weights̲positive この関数は,rational̲b̲spline̲curveの制御点に関係付けられた重みを調べ,
これらの重みがすべて正であればTRUEを返す。
EXPRESSによる定義
*)
FUNCTION curve̲weights̲positive(b: rational̲b̲spline̲curve) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END̲LOCAL;
REPEAT i := 0 TO b.upper̲index̲on̲control̲points;
IF b.weights[i] <= 0.0 THEN
result := FALSE;
RETURN(result);
END̲IF;
END̲REPEAT;
RETURN(result);
END̲FUNCTION;
(*
引数定義
b:(入力)重みの値を検査するrational̲b̲spline̲curve。
4.6.24 constraints̲composite̲curve̲on̲surface この関数は,composite̲curve̲on̲surfaceのセグメントか
ら参照される曲線が,すべてcurve̲on̲surfaceであることを検査する。curve̲on̲surfaceは,bounded̲curve
であるcomposite̲curve̲on̲surface型を含む。
EXPRESSによる定義
99
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
FUNCTION constraints̲composite̲curve̲on̲surface
(c: composite̲curve̲on̲surface) : BOOLEAN;
LOCAL
n̲segments : INTEGER := SIZEOF(c.segments);
END̲LOCAL;
REPEAT k := 1 TO n̲segments;
IF (NOT('GEOMETRY̲SCHEMA.PCURVE' IN
TYPEOF(c\composite̲curve.segments[k].parent̲curve))) AND
(NOT('GEOMETRY̲SCHEMA.SURFACE̲CURVE' IN
TYPEOF(c\composite̲curve.segments[k].parent̲curve))) AND
(NOT('GEOMETRY̲SCHEMA.COMPOSITE̲CURVE̲ON̲SURFACE' IN
TYPEOF(c\composite̲curve.segments[k].parent̲curve))) THEN
RETURN (FALSE);
END̲IF;
END̲REPEAT;
RETURN(TRUE);
END̲FUNCTION;
(*
引数定義
c:(入力)検査するcomposite̲curve̲on̲surface。
4.6.25 get̲basis̲surface この関数は,曲線のbasis̲surfaceを,surfaceの集合として返す。曲線が
curve̲on̲surfaceでない場合は,空集合を返す。
EXPRESSによる定義
*)
FUNCTION get̲basis̲surface (c : curve̲on̲surface) : SET[0:2] OF surface;
LOCAL
surfs : SET[0:2] OF surface;
n
: INTEGER;
END̲LOCAL;
surfs := [];
IF 'GEOMETRY̲SCHEMA.PCURVE'IN TYPEOF (c) THEN
surfs := [c\pcurve.basis̲surface];
ELSE
IF 'GEOMETRY̲SCHEMA.SURFACE̲CURVE' IN TYPEOF (c) THEN
n := SIZEOF(c\surface̲curve.associated̲geometry);
REPEAT i := 1 TO n;
surfs := surfs +
associated̲surface(c\surface̲curve.associated̲geometry[i]);
END̲REPEAT;
100
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲IF;
END̲IF;
IF 'GEOMETRY̲SCHEMA.COMPOSITE̲CURVE̲ON̲SURFACE' IN TYPEOF (c) THEN
(* composite̲curve̲on̲surface の basis̲surface は,
すべてのセグメントの basis̲surface の積となる。*)
n := SIZEOF(c\composite̲curve̲on̲surface.segments);
surfs := get̲basis̲surface(c\
composite̲curve̲on̲surface.segments[1].parent̲curve);
IF n > 1 THEN
REPEAT i := 2 TO n;
surfs := surfs *
get̲basis̲surface(c\
composite̲curve̲on̲surface.segments[i].parent̲curve);
END̲REPEAT;
END̲IF;
END̲IF;
RETURN(surfs);
END̲FUNCTION;
(*
引数定義
c:(入力)basis̲surfaceを定めるcurve。
surfs:(出力)basis̲surface又はcを含む曲面からなる集合。
4.6.26 surface̲weights̲positive この関数は,rational̲b̲spline̲surfaceの制御点に関係付けられた重みを
調べ,これらの重みがすべて正であればTRUEを返す。
EXPRESSによる定義
*)
FUNCTION surface̲weights̲positive(b: rational̲b̲spline̲surface) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END̲LOCAL;
REPEAT i := 0 TO b.u̲upper;
REPEAT j := 0 TO b.v̲upper;
IF (b.weights[i][j] <= 0.0) THEN
result := FALSE;
RETURN(result);
END̲IF;
END̲REPEAT;
END̲REPEAT;
RETURN(result);
END̲FUNCTION;
101
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(*
引数定義
b:(入力)重みの値を検査するrational̲b̲spline̲surface。
4.6.27 constraints̲rectangular̲composite̲surface この関数は,rectangular̲composite̲surfaceの属性に関
して,次の制約を検査する。
− 構成要素の曲面は,すべてrectangular̲trimmed̲surface又はb̲spline̲surfaceのいずれかとする。
− セグメントの配列の属性transitionは,discontinuousという値を含まない。ただし,最後の行又は
最後の列は,その限りではない。discontinuousの場合は,対応する方向に関して,曲面が閉じて
いないことを示す。
EXPRESSによる定義
*)
FUNCTION constraints̲rectangular̲composite̲surface
(s : rectangular̲composite̲surface) : BOOLEAN;
(* surface の型を検査する。*)
REPEAT i := 1 TO s.n̲u;
REPEAT j := 1 TO s.n̲v;
IF NOT(('GEOMETRY̲SCHEMA.B̲SPLINE̲SURFACE' IN TYPEOF
(s.segments[i][j].parent̲surface)) OR
('GEOMETRY̲SCHEMA.RECTANGULAR̲TRIMMED̲SURHACE' IN TYPEOF
(s.segments[i][j].parent̲surface))) THEN
RETURN(FALSE);
END̲IF;
END̲REPEAT;
END̲REPEAT;
(* transition̲code を検査する。最後の行及び最後の列は除く。*)
REPEAT i := 1 TO s.n̲u-1;
REPEAT j := 1 TO s.n̲v;
IF s.segments[i][j].u̲transition = discontinuous THEN
RETURN(FALSE);
END̲IF;
END̲REPEAT;
END̲REPEAT;
REPEAT i := 1 TO s.n̲u;
REPEAT j := 1 TO s.n̲v-1;
IF s.segments[i][j].v̲transition = discontinuous THEN
RETURN(FALSE);
END̲IF;
END̲REPEAT;
END̲REPEAT;
RETURN(TRUE);
102
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲FUNCTION;
(*
引数定義
s:(入力)検査するrectangular̲composite̲surface。
4.6.28 list̲to̲array この関数list̲to̲arrayは,総称データ型のリストを,あらかじめ添字の範囲が決めら
れている配列に変換する。添字の要素数が元のリストの要素数と一致しない場合には,結果として不定“?”
が返される。この関数は,B-スプラインのエンティティ定義において用いられる制御点及び重みの配列を
作るために使われる。
EXPRESSによる定義
*)
FUNCTION list̲to̲array(lis : LIST [0:?] OF GENERIC : T;
low,u : INTEGER) : ARRAY[low:u] OF GENERIC : T;
LOCAL
n
: INTEGER;
res : ARRAY [low:u] OF GENERIC : T;
END̲LOCAL;
n := SIZEOF(lis);
IF (n <> (u-low +1)) THEN
RETURN(?);
ELSE
REPEAT i := 1 TO n;
res[low+i-1] := lis[i];
END̲REPEAT;
RETURN(res);
END̲IF;
END̲FUNCTION;
(*
引数定義
lis:(入力)変換するリスト。
low:(入力)出力配列の添字の下限を指定する整数。
u:(入力)添字の上限を指定する整数。
res:(出力)入力データから生成された配列。
4.6.29 make̲array̲of̲array この関数make̲array̲of̲arrayは,リストのリストから2次元の配列を作る。
この関数は,まず与えられた配列の大きさがリストの大きさと一致するかどうかを検査し,次にすべての
部分リストの要素の個数が一致することを確かめる。それらが一致しない場合には,結果として不定“?”
が返される。この関数は,B-スプライン曲面の制御点及び重みの配列を作るために使われる。
EXPRESSによる定義
*)
FUNCTION make̲array̲of̲array(lis : LIST[1:?] OF LIST [1:?] OF GENERIC : T;
low1, u1, low2, u2 : INTEGER):
103
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ARRAY[low1:u1] OF ARRAY [low2:u2] OF GENERIC : T;
LOCAL
n1,n2 : INTEGER;
res
: ARRAY[low1:u1] OF ARRAY [low2:u2] OF GENERIC : T;
res1 :LIST[1:?] OF ARRAY [low2:u2] OF GENERIC : T;
END̲LOCAL;
(* リストの大きさと配列の大きさとの整合性を検査する。*)
n1 := SIZEOF(lis);
n2 := SIZEOF(lis[1]);
IF (n1 <> (u1-low1 + 1)) AND (n2 <> (u2 - low2 + 1)) THEN
RETURN(?);
END̲IF;
REPEAT i := 1 TO n1;
IF (SIZEOF(lis[i]) <> n2) THEN
RETURN(?);
END̲IF;
END̲REPEAT;
(* 部分配列のリストを作る。*)
REPEAT i := 1 TO n1;
RESL[i] := list̲to̲array(lis[i],low2,u2);
END̲REPEAT;
res := list̲to̲array(res1,low1,u1);
RETURN(res);
END̲FUNCTION;
(*
引数定義
lis:(入力)変換するリストのリスト。
low1:(入力)出力配列の第1の添字の下限を指定する整数。
u1:(入力)第1の出力配列の添字の上限を指定する整数値。
low2:(入力)出力配列の第2の添字の下限を指定する整数。
u2:(入力)第2の出力配列の添字の上限を指定する整数値。
res:(出力)整合性を検査した入力データから生成された2次元配列。これは,指定された大きさをもつ。
EXPRESSによる定義
*)
END̲SCHEMA; -- geometry̲schemaの終了
(*
5. 位相(Topology) 次のEXPRESS宣言は,topology̲schemaを開始し,必要な外部参照を明らかにする。
EXPRESSによる定義
*)
104
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SCHEMA topology̲schema;
REFERENCE FROM geometry̲schema;
REFERENCE FROM representation̲schema(representation̲item);
(*
備考1. 上で参照しているスキーマは,次の規格による。
geometry̲schema この規格の4.
representation̲schema JIS B 3700-43
2. このスキーマの図式表現を附属書Dの図D.13〜D.15に示す。
5.1
概要 位相リソースモデルは,境界表現の立体モデルの考え方を基にしたものであるが,それ以外
の応用でも,接続関係を直接表現する方法が必要な場合に用いることかできる。
5.2
基本概念及び前提条件 この規格で規定するvertex,edgeなどの位相エンティティは,これらの使
用法とは独立に定義する。各エンティティには最小限の制約だけが課され,それ以上の制約は,これらを
用いるエンティティによって,又はエンティティが用いられる前後関係によって定義される。これは,エ
ンティティを用いる際に,その前後関係及び使用法を制限しないことを意図している。
位相エンティティは,vertexを基本的なエンティティとして階層的に定義する。すなわち,その他の位
相エンティティは,vertexによって直接的に又は間接的に定義される。
エンティティは,それぞれか制約の集合をもつ。位相的な階層関係において上位のエンティティは,下
位のエンティティに制約を課すことができる。上位からみると,下位のエンティティに課される制約は,
上位から下位までの各エンティティに課される制約の総和となる。基本的な位相エンティティの構造は,
複雑さの増加する順に,vertex,edge,path,loop,face及びshellとなる。高水準に構造化された位相エン
ティティのopen̲shell及びclosed̲shellは,connected̲face̲setの特殊な下位型とする。ここでは,ほかに
connected̲edge̲set及び単純なconnected̲face̲setを定義する。これら2種類のエンティティは,shellに対
する制約を課すことが適当でない位相データの集まりの交換に使われる。
poly̲loopは,直線状かつ共面の稜線のループとし,順序付けられた点のリストとして定義する。poly̲loop
エンティティは,多面体境界表現モデルのデータ交換に用いられる。
エンティティに位相的及び幾何的な制約を加えて,位相モデルの一貫性を保証するために多くの関数を
用意する。
5.2.1
幾何との関連付け 位相エンティティの多くは,特殊な下位型によって幾何データと結び付けるこ
とができる。境界表現立体モデルをデータを交換する際には,この結び付きが必要不可欠となる。vertex,
edge及びfaceの特殊な下位型は,それぞれvertex̲point,edge̲curve,face̲surfaceとする。edge̲curve及び
face̲surfaceについては,結び付けられたエンティティの幾何的な向きと位相的な向きとの関係も記録され
る。定義域の概念が,幾何を位相に関連付ける。point,curve又はsurfaceの定義域は,単純にその点(point),
曲線(curve)又は曲面(surface)とする。vertex,edge又はfaceの定義域は,対応する点,曲線又は曲面
とする。loop又はpathの定義域は,そのloop又はpathに含まれるすべてのvertex及びedgeの定義域の和
とする(vertex̲loopの場合を除き,定義域は,一つの曲線となる。)。shellの定義域は,そのshellに含ま
れるすべてのvertex,edge及びfaceの定義域の和とする(closed̲shell又はopen̲shellの場合,定義域は,
曲面となる。)。立体モデルの定義域は,それが占める空間の領域とする。SET又はLISTの定義域は,そ
のSET又はLISTの要素の定義域の和とする。この規格を利用して,あるエンティティに関して連結性,
有限性などの幾何的概念を議論する場合,その概念は,エンティティの定義域に適用されるものとする。
定義域を記述する際の主要な概念は,多様体の考え方とする。直観的にいうと,定義域がd次元ユーク
105
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
リッド空間と局所的に区別不能であれば,その定義域は,d-多様体とする。このことは,次元数が定義域
の各点で同じであり,定義域には自己干渉が許されないことを意味する。この規格では,curve及びsurface
は,自己干渉を含むことができるので,多様体とは限らない。しかし,curve又はsurfaceの中で,edge,
faceのような位相エンティティの定義域に対応する部分は,多様体でなければならない。
この規格では,“多様体”,“境界”及び“境界付き多様体”は,通常の数学的な定義と同一とする。境界
付き多様体が多様体と異なるのは,境界が存在してもよい点にある。
1-多様体は,自己干渉しない曲線となり,その終了点を含まない。1-多様体の例として,実数直線及び
単位円がある。“Y”字型をした図形及び単位閉区間は,1-多様体ではない。2-多様体は,境界曲線を含ま
ず,自己干渉しない曲面となる。2-多様体の例として,単位球面及び開円盤 {(x,y,0):x2+y2<1} がある。
閉円盤 {(x,y,0):x2+y2≦1} は,多様体ではない。稜線及び稜線列は,定義域が存在するならば,1-多様体
となる。面及び閉シェルは,定義域が存在するならば,2-多様体となる。
自己干渉しない曲線は,境界付き1-多様体となる。閉円盤 {(x,y,0):x2+y2≦1} は,境界付き2-多様体
となる。開シェルは,定義域か存在するならば,境界付き2-多様体となる。多様体立体境界表現又は多面
体多様体境界表現の定義域は,境界付き3-多様体となる。
境界付きd-多様体の境界は,(d−1)-多様体となる。例えば,曲線の境界は,その曲線に含まれる0〜2
個の終了点の集合となる。閉円盤 {(x,y,0):x2+y2≦1} の境界は,単位円となる。開シェルの定義域の境
界は,シェルの穴を囲むループの集合となる。多様体立体境界表現又は多面体多様体境界表現の境界は,
境界シェルの集合の定義域となる。
境界付き多様体である曲線及び曲面は,開又は閉に分類できる。この規格において,用語“開”及び“閉”
が曲線又は曲面に対して用いられた場合,点集合位相幾何学における“開集合”又は“閉集合”の概念と
混同してはならない。“閉曲面”という用語は,閉,連結,かつ向き付け可能な2-多様体の通常の定義と
同一とする。閉曲面の例として,球面及び輪環面がある。閉シェルは,定義域が存在するならば,閉曲面
となる。開曲面の例として,無限平面及び1個以上の穴をもった曲面がある。開シェルは,定義域が存在
する場合,開曲面となる。
現実に製作可能なすべての閉曲面は,向き付け可能となる。面の定義域は,常に平面に埋込み可能であ
り,したがって,向き付け可能となる。開曲面は,向き付け可能とは限らない。例えば,メビウスの輪は,
開曲面である。更に,この規格の定義では,開でも閉でもない多様体がある。クラインのつぼ(壷)が,
その例である。クラインの壼は,有限で境界が存在しないか,向き付け可能ではないので,空間を2個の
領域に分割しない。しかし,この規格で定義される開シェルの定義域は,向き付け可能でなければならな
い。
用語“種数”は,エンティティの位相的な性質の分類に用いる整数値を指す。この規格では2種類の種
数を定義する。
edge及びvertexからなるグラフとみなせるエンティティ,例えば,loop,path又はwire̲shellについて
は,種数は,グラフ理論における“サイクル階数”と同値とする。グラフ理論における“種数”とは異な
る。直観的には,種数は,グラフにおける独立サイクルの数を示す。例えば,1個の頂点だけからなり,n
個の自己ループからなるグラフの種数は,nとなる。
閉曲面Xの種数とは,Xに位相同型な曲面を生成するために球面に加えなければならないハンドルの個
数とする。例えば,球面の種数は0,輪環体の種数は1である。種数は,代数的位相幾何学における“曲
面の種数”と同一とする。閉曲面にハンドルを加えることは,その曲面によって囲まれた3次元の領域に
貫通穴を開ける操作となる。この操作は,2個の円盤を切り抜き,それらの境界を円柱状の管でつなぐ操
106
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
作とみることかできる。“ハンドル”は,“穴”とは異なる。この規格では,用語“穴”は,2次元の曲面
に穴をあけるという直観的な概念に対応する。
曲面の種数の定義は,次のように向き付け可能な開曲面に拡張できる。定義域の穴をすべて円盤でふさ
ぐと,閉曲面が得られる。この閉曲面については,既に種数が定義されている。この閉曲面の種数を開曲
面の種数とする。
5.2.2
パラメタ空間幾何との関連付け ここでの基本的な仮定として,定義される位相は,モデル空間の
位相とする。曲線及び点の幾何は,パラメタ空間中で定義することができる。しかし,一般には,パラメ
タ空間における位相構造は,その基礎となるモデル空間の位相構造とは必ずしも一致しない。faceとその
基礎となるsurfaceとの関係が,その例である。
パラメタ空間系は,幾何を位相に関連させる方法論において実空間系とは異なっている。典型的にはパ
ラメタ空間系は,異なったパラメタ空間曲線をそれぞれのedge use(すなわち,oriented̲edge)に関連させ
る。(edge useの方法の)既知の稜線に関連したパラメタ空間曲線の実空間のすべての同じ点を表現する。
各パラメタ空間曲線は,それぞれ異なったパラメタ空間で定義される。そのパラメタ空間は,その稜線が
境界付ける面の基礎をなす曲面とする。多様体立体では,すべてのedgeの幾何は,そのedgeを境界とし
てもつ二つのfaceのそれぞれに対して1回ずつ,計2回定義される。
参考 edge useとは,稜線(edge)が曲面やループから参照される際に,その用いられる方向を
明示するための補助的なデータである。これは,立体モデルなどで,稜線に関する隣接関
係を効率的に表現するのに適する。立体モデルの内部表現に用いる場合,一つの稜線には,
方向が異なる一対のedge useが対応する。
各edge useにパラメタ空間曲線を関連付けることは,自然に縮退稜線(すなわち,実空間では長さが0
の稜線)の使用につながる。例えば,パラメタ空間系が,実空間で三角形である面を,パラメタ空間では
長方形で表現したいとする。このための直接的な方法は,三角形面の頂点の一つを縮退稜線(しかし,二
つの頂点をもつ。)として表現することである。そうすれば,実空間の稜線とモデル空間の稜線との間に一
対一の対応がとれる。縮退稜線は,実空間では長さ0であるが,パラメタ空間では,0を超える長さをも
つ。縮退稜線は,円錐の頂点のような特異点のまわりに境界を設けるために用いてもよい。
実空間系は,各edge useにパラメタ空間曲線を関連付けさせず,縮退稜線も許さない。パラメタ空間系
の位相の扱いは,実装上の都合であるため,この規格では,実空間位相を使う。パラメタ空間系における
一意な情報は,(edge useを使用しなくても)幾何を用いることによって得られる。
5.2.2.1
edge̲curveのパラメタ空間曲線との関連付け パラメタ空間曲線と一つのedge̲curveとを関連付
けるために用いることのできる技術は,次のとおりとする。
(a) edge̲curveの属性edge̲geometryは,一つのpcurveを直接参照してもよい。そのとき,そのedge̲curve
にはただ一つのpcurveが関連付けられる。
(b) edge̲curveの属性edge̲geometryは,surface̲curve,又はsurface̲curveの下位型を参照することができ
る。そのとき,そのedge̲curveには,そのsurface̲curveの属性associated̲geometryで参照された(1
〜2個の)pcurveが関連付けられる。そのsurface̲curveの属性curve̲3dによって参照された曲線も,
そのedge̲curveに関連付けられる。しかし,その曲線は,パラメタ空間曲線ではありえず,そのedge
のモデル空間での幾何を表現する。
(c) edge̲curveの属性edge̲geometryは,(pcurveではない)曲線を参照することができる。そのとき,そ
のedge̲curveには0回以上のpcurveが関連付けられる。そのpcurveとは,当該の曲線を属性curve̲3d
として参照するsurface̲curveが,属性associated̲geometryとして参照するものである。
107
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
このために,関数edge̲curve̲pcurvesがEXPRESSで形式的に定義されている。この関数は,ある特定の
edgeに関連付けられているすべてのパラメタ空間曲線を決定するために用いることができる。
備考1. パラメタ空間曲線を理解しなくてもよい実空間系の応用のためには,パラメタ空間系は,上
の(c)だけを用いるのがよい。そうすれば,pcurveを無視しても実空間系では,すべての
edge̲curveは,それに関連付けられた正しい幾何をもつ。
2. あるedge̲curveのpcurveが与えられたとき,どのoriented̲edgeにそのpcurveが関連付けら
れるかを求めるとする。それは,そのoriented̲edgeの囲む面のface̲geometryが,そのpcurve
のbasis̲surfaceにインスタンス等価なものを見つける問題となる。あるedge̲curveに関連づ
けられた2個以上のpcurveが,同じ曲面のパラメタ空間で定義されているとする。そのとき,
pcurveが関連付けられるoriented̲edgeを決定するためには,パラメタ空間でのpcurveの接続
関係を調べる必要がある。
5.2.3
グラフ,サイクル及び通過 グラフの連結構成要素とは,そのグラフの連結部分集合であり,それ
より大きな連結部分集合に属さないものとする。連結構成要素の個数をグラフの多重度と呼び,Mで表す。
したがって,グラフが連結であるための必要十分条件は,M=1となる。
グラフの各構成要素は,始め及び終わりを同じ頂点にして,次のように完全に通過できる。すべての稜
線は,各方向に1回ずつ計2回通過され,すべての頂点は,その頂点を用いる稜線の数と同じ回数だけ通
過される。(稜線+稜線の通過する方向)を単位と考えれば,それぞれ一意に定まる(稜線+方向)の組合
せは,グラフの通過においてそれぞれ1回だけ現れる。グラフを通過すると,頂点及び(稜線+方向)単
位は,交互に現れて閉サイクルを構成する。その閉サイクルは,1個以上存在する。
記号Gは,グラフの種数を表す。これは直観的には,グラフにおける独立サイクルの個数となる[専門
的には,Gは,グラフの基本群(fundamental group)の階数となる。]。
すべてのグラフは,次のオイラー式を満たす。
(ν−ε)−(M−G)=0 ······································································ (1)
ここで,ν及びεは,グラフにおける一意な頂点及び稜線の個数とする。
備考 グラフを通過し,M及びGを計算するのに,次のグラフ通過アルゴリズム(附属書E4.参
照)を用いることかできる。
(a) M及びGを0にする。
(b) (まだ通っていない)任意の頂点から始める。まだ通っていない頂点がなければ停止
する。当該の頂点に通過済みの印を付け,Mに1を加える。その頂点から任意の稜線
を通過し,その稜線に通過方向の印を付ける。
(c) 稜線PQを通過して頂点Qに到達したところで,次の操作を行う。
− その頂点に初めて到達した場合には,稜線に頂点Qの初進入稜線の印を付ける。
初進入稜線の印は,稜線がその方向で1回だけしか選ばれないようにするための
ものである。
− 頂点Qに通過済みの印を付ける。
− 稜線PQにとって最初の通過であり,かつ頂点Qが通過済みの場合には,Gに1
を加える。
− 頂点Qから出る稜線を次の規則に従って選ぶ。
(1) 頂点Qから出て行く方向で既に通過した稜線は,選べない。
(2) 1を満たす稜線で,Qの初進入稜線以外のものを選ぶ。
108
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(3) 2を満たす稜線がない場合には,初進入稜線を選ぶ。
− 稜線か選ばれたら,その稜線を通過し,更にその稜線に通過方向の印を付ける。
(d) (c)で稜線が選ばれた場合には(c)を行い,稜線が1個も選ばれなかった場合には(b)を行
う。
5.3
topology̲schemaの型定義
5.3.1
shell shellは,より複雑なモデルを構築する際の参考のためのもので,シェルとしての特徴をもつ
下位型を集めた型とする。これは,領域を境界付けするのに通常用いられるd=0,1,又は2に固定された次
元数の連結オブジェクトとする。shellの定義域は,存在する場合,自身の境界を含み,かつ0≦Ξ<∞と
なる。次元数0のshellは,単一の頂点から構成されるグラフによって表現される。vertexは,関連付けら
れたedgeをもってはならない。次元数1のshellは,次元数1の連結グラフによって表現される。次元数
2のshellは,edgeに沿って接続する面によって構成される位相エンティティとする。その定義域は,存在
する場合,連結された,向き付け可能な境界を伴った2-多様体とする。すなわち,閉又は開のいずれでも
よく,自己干渉しない,連結,向き付けかつ有限な曲面となる。
EXPRESSによる定義
*)
TYPE shell = SELECT
(vertex̲shell,
wire̲shell,
open̲shell,
closed̲shell);
END̲TYPE;
(*
5.3.2
reversible̲topology̲item reversible̲topology̲itemは,向きを反転する操作に関連したすべての位
相表現要素を表す。これは,関数conditional̲reverseによって用いられる。
EXPRESSによる定義
*)
TYPE reversible̲topology̲item = SELECT
(edge,
path,
face,
face̲bound,
closed̲shell,
open̲shell);
END̲TYPE;
(*
5.3.3
list̲of̲reversible̲topology̲item list̲of̲reversible̲topology̲itemは,reversible̲topology̲itemのリス
トを定義する。これは,関数list̲of̲topology̲reversedによって用いられる。
EXPRESSによる定義
*)
TYPE list̲of̲reversible̲topology̲item =
109
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LIST [0:?] of reversible̲topology̲item;
END̲TYPE;
(*
5.3.4
set̲of̲reversible̲topology̲item set̲of̲reversible̲topology̲itemは,reversible̲topology̲itemの集合
を定義する。これは,関数set̲of̲topology̲reversedによって用いられる。
EXPRESSによる定義
*)
TYPE set̲of̲reversible̲topology̲item
= SET [0:?] of reversible̲topology̲item;
END̲TYPE;
(*
5.3.5
reversible̲topology reversible̲topologyは,すべてのreversible̲topology̲itemの型を明らかにする。
これは,関数topology̲reversedによって用いられる。
EXPRESSによる定義
*)
TYPE reversible̲topology = SELECT
(reversible̲topology̲item,
list̲of̲reversible̲topology̲item,
set̲of̲reversible̲topology̲item);
END̲TYPE;
(*
5.4
topology̲schemaのエンティティ定義 ここては,topology̲schemaで使われるすべてのエンティテ
ィ定義を定義する。
5.4.1
topological̲representation̲item topological̲representation̲itemは,オブジェクトの表現を構成する
エンティティの位相,すなわち,接続関係を表現する。topological̲representation̲itemは,位相スキーマに
おけるすべてのrepresentation̲itemの上位型とする。
EXPRESSによる定義
*)
ENTITY topological̲representation̲item
SUPERTYPE OF (ONEOF(vertex, edge, face̲bound, face, vertex̲shell,
wire̲shell, connected̲edge̲set, connected̲face̲set,
(loop ANDOR path)))
SUBTYPE OF (representation̲item);
END̲ENTITY;
(*
非形式的要件
IP1:各topological̲representation̲itemについて,そのtopological̲representation̲itemが直接的に又は再帰的
に参照するvertex̲point,edge̲curve及びface̲surfaceの集合を考える(この集合にはoriented̲edge又はface
は含まないが,それらの元の向き付けされていないedge及びfaceは含む。)。この場合,集合から異な
る二つの要素をとったとき,その定義域は,互いに交差してはならない。
110
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.4.2
vertex vertex(頂点)は,点に対応する位相の構成要素とする。その次元数及び大きさは,0とす
る。頂点の定義域は,存在する場合,m次元実空間Rmにおける点とする。これは,下位型のvertex̲point
によって表現される。
EXPRESSによる定義
*)
ENTITY vertex
SUBTYPE OF (topological̲representation̲item);
END̲ENTITY;
(*
非形式的要件
IP1:vertexの次元数は,0とする。これは,vertexの基本的な性質とする。
IP2:vertexの大きさは,0と定義する。
5.4.3
vertex̲point vertex̲pointは,pointとして定義された幾何をもつvertexとする。
EXPRESSによる定義
*)
ENTITY vertex̲point
SUBTYPE OF (vertex, geometric̲representation̲item);
vertex̲geometry : point;
END̲ENTITY;
(*
属性定義
vertex̲geometry:vertexの幾何空間における位置を定義する幾何の点。
非形式的要件
IP1:vertexの定義域は,そのvertex̲geometryの定義域であるとして形式的に定義される。
5.4.4
edge edge(稜線)は,二つのvertex間の連結に対応する位相の構成要素とする。より抽象的には,
それは,二つのvertex間の論理的な関係を表すとしてもよい。edgeの定義域は,存在する場合,Rmにおけ
る有限かつ自己干渉しない開曲線,すなわち,連結1次元多様体とする。edgeの境界は,二つのvertexと
し,これらは異なっている必要はない。edgeは,1番目のvertexから2番目のvertexへ通過する方向に向
き付けされる。二つのvertexが同一の場合,そのedgeは,自己ループとする。edgeの定義域は,その境
界を含まず,かつ0<Ξ<∞とする。edgeには,そのedgeを座標空間内に配置するため幾何のcurveを関
連付けることができる。これは,下位型のedge̲curveによって表現する。このcurveは,edgeの定義域内
においては有限とし,かつ自己干渉してはならない。edgeはグラフであるので,その多重度M及びグラフ
の種数Geはグラフ通過アルゴリズムによって決定される。M=ε=1であるので,式(1)は,この場合,次の
とおりになる。
ν−(2−Ge)=0 ············································································ (2)
ここで,ν=1又は2とし,並びに,Ge=1又は0とする。
特に,位相としてのedgeは,次項を満足しなければならない。
− edgeは,二つのvertexをもち,
|E[V]|=2
− それらのvertexは,異なっている必要はなく,
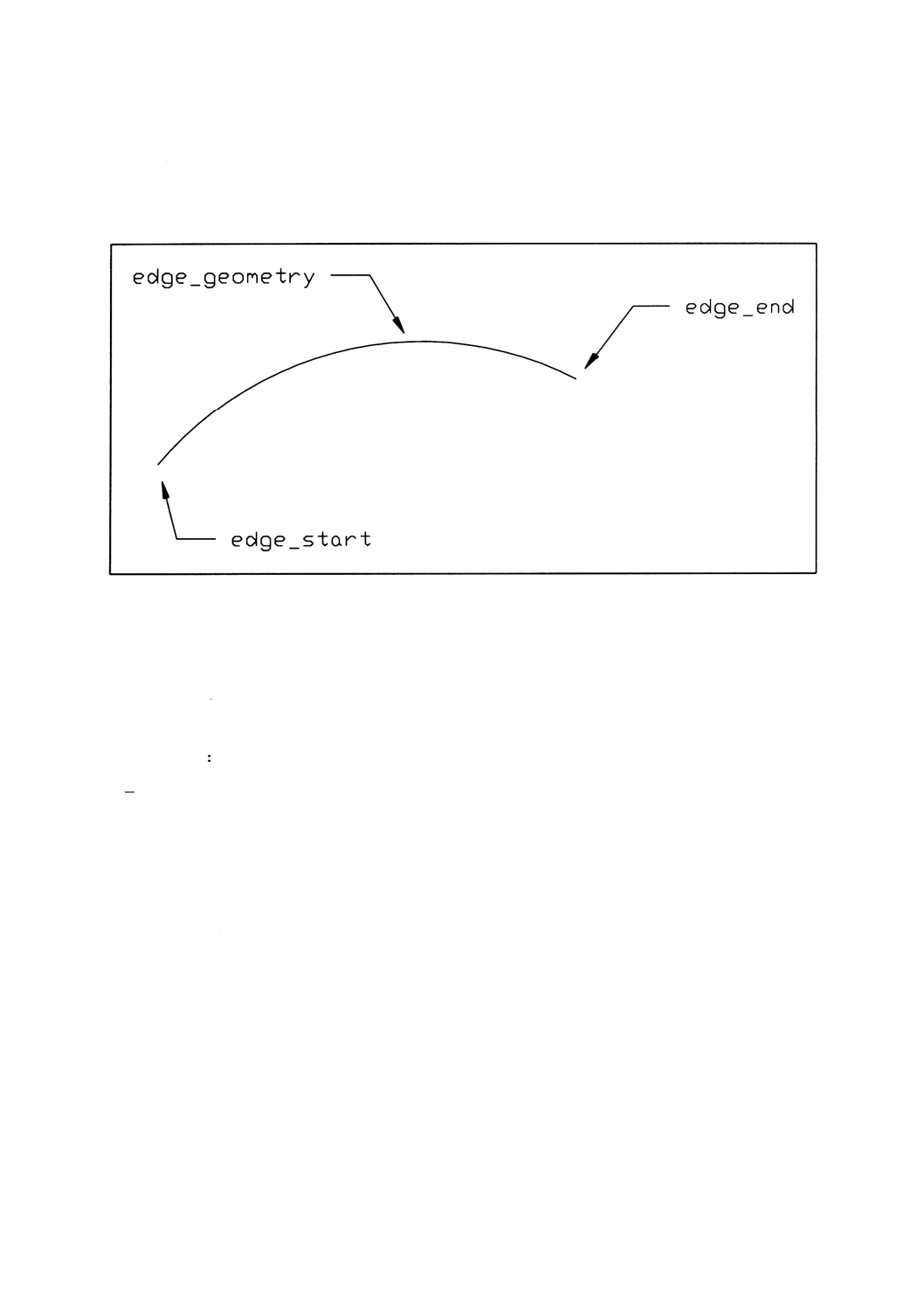
111
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1≦|E{V}|≦2
− 式(2)が成り立つ。
|E{V}|−2+Ge=0
図11 edge̲curve
EXPRESSによる定義
*)
ENTITY edge
SUPERTYPE OF (ONEOF(edge̲curve, oriented̲edge))
SUBTYPE OF (topological̲representation̲item);
edge̲start : vertex;
edge̲end : vertex;
END̲ENTITY;
(*
属性定義
edge̲start:edgeの開始点(vertex)。
edge̲end:edgeの終了点(vertex)。edge̲start及びedge̲endの両方に同一のvertexを用いることかできる。
非形式的要件
IP1:edgeの次元数は,1とする。
IP2:edgeの大きさは,有限とし,かつ0でないとする。
5.4.5
edge̲curve edge̲curveは,edgeの特殊な下位型とし,完全に定義された幾何をもつ。その幾何は,
edgeがcurveと関連付けられることによって定義される。そのcurveは,境界がなくてもよい。位相の方
向と幾何の方向とは,逆でもよい。edgeの方向とcurveの方向とが一致するか逆であるかを示すために,
識別子(same̲sense)が使われる。このブール値は,curveの方向とedgeの方向が,一致するか(TRUE),
又は逆であるか(FALSE)のいずれかを示す。edgeのvertexに関連付けられたあらゆる幾何は,edgeの幾
何と整合しなければならない。複数のedgeは,同じcurveを参照することかできる。
EXPRESSによる定義
112
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
ENTITY edge̲curve
SUBTYPE OF (edge,geometric̲representation̲item);
edge̲geometry
: curve;
same̲sense : BOOLEAN;
END̲ENTITY;
(*
属性定義
edge̲geometry:edgeの形状及び空間的な配置を定義するcurve。このcurveは,境界がなくてもよく,edge
のvertexによって暗黙にトリムされる。これは,edgeの定義域を定める。
same̲sense:このブール型のフラグは,edgeの向きとedgeの幾何を定義するcurveの向きとが,同じであ
るか(TRUE),又は逆であるか(FALSE)のいずれかを示す。edgeの向きは,edgeの開始vertexからedge
の終了vertexへの向きとする。curveの向きは,パラメタの増加する方向とする。
備考 属性の実例については,図11参照。
非形式的要件
IP1:edge̲curveの定義域は,そのedge̲geometryの定義域をvertexでトリムしたものとして形式的に定義
される。この定義域は,vertexを含まない。
IP2:edge̲curveの大きさは,有限とし,かつ0でないとする。
IP3:edge̲curveは,多様体とする。
IP4:edge̲curveは,弧状連結とする。
IP5:edge̲startは,edgeの定義域に含まれない。
IP6:edge̲endは,edgeの定義域に含まれない。
IP7:vertexの幾何は,edgeの幾何と整合しなければならない。
5.4.6
oriented̲edge oriented̲edgeは,別のedgeから構成されるedgeとする。これは,その向きと元の
edgeの向きとが一致するか否かを示すブール型の向きフラグをもつ。向きに関する属性を除けば,
oriented̲edgeは,元のedgeと等価になる。
備考 立体モデリングシステムは,一般に,edgeの“edge use”,すなわち,“通過”を表現する
エンティティをもつ。この“edge use”エンティティでは,各edgeがそれぞれの方向に1
回ずつ計2回通過されなければならない,という多様体立体の要件を明示的に表現する。
“edge use”の機能は,edgeの下位型のoriented̲edgeで用意される。
EXPRESSによる定義
*)
ENTITY oriented̲edge
SUBTYPE OF (edge);
edge̲element
: edge;
orientation : BOOLEAN;
DERIVE
SELF\edge.edge̲start : vertex := boolean̲choose (SELF.orientation,
SELF.edge̲element.edge̲start,
SELF.edge̲element.edge̲end);
113
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SELF\edge.edge̲end : vertex := boolean̲choose (SELF.orientation,
SELF.edge̲element.edge̲end,
SELF.edge̲element.edge̲start);
WHERE
WR1: NOT ('TOPOLOGY̲SCHEMA.ORIENTED̲EDGE' IN TYPEOF (SELF.edge̲element));
END̲ENTITY;
(*
属性定義
edge̲element:このoriented̲edgeを構成するために用いられるエンティティedge。
orientation:ブール型の属性。TRUEの場合,位相上の向きは,edge̲elementの開始vertexから終了vertex
への向きに一致する。
edge̲start:oriented̲edgeの開始vertex。これは,orientationを考慮してedge̲elementのvertexから導出され
る。
edge̲end:oriented̲edgeの終了vertex。これは,orientationを考慮してedge̲elementのvertexから導出され
る。
形式的要件
WR1:edge̲elementは,oriented̲edgeであってはならない。
5.4.7
path pathは,oriented̲edgeの順序付けられた集まりからなる位相エンティティとする。ここで,
各edgeのedge̲startのvertexは,その一つ手前のedgeのedge̲endのvertexに一致する。pathは,最初の
oriented̲edgeのedge̲startから最後のoriented̲edgeのedge̲endの順に順序付けられる。oriented̲edgeのブ
ール値orientationは,edgeの方向がpathの方向に一致するか(TRUE),又は逆の方向であるか(FALSE)
のいずれかを示す。
個々のedgeは,個々のpathによって1回だけ参照できる。
edgeは,複数のpathによって参照できる。edgeは,pathと独立に存在できる。
EXPRESSによる定義
*)
ENTITY path
SUPERTYPE OF (ONEOF(open̲path, edge̲loop, oriented̲path))
SUBTYPE OF (topological̲representation̲item);
edge̲list : LIST [1:?] OF UNIQUE oriented̲edge;
WHERE
WR1: path̲head̲to̲tail(SELF);
END̲ENTITY;
(*
属性定義
edge̲list:pathを構成するために接合されるエンティティoriented̲edgeのリスト。
形式的要件
WR1:各oriented̲edgeの終了vertexは,その次のedgeの開始vertexと同じでなければならない。
非形式的要件
IP1:pathの次元数は,1とする。
114
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IP2:pathは,弧状連結とする。
IP3:共通するvertexを除き,pathのedgeは,互いに交差しない。
IP4:pathの大きさは,有限かつ0でない。
IP5:いかなるpathも,同じedge̲elementで,かつ同じorientationをもつoriented̲edgeを二つ含むことは
ない。
5.4.8
oriented̲path oriented̲pathは,別のpathから構成されたpathで,構成されたpathの向きと元の
pathの向きが一致するか否かを示すブール型の向きフラグをもつ。向きに関する点を除けば,oriented̲path
は,元のpathと等価とする。
EXPRESSによる定義
*)
ENTITY oriented̲path
SUBTYPE OF (path);
path̲element
: path;
orientation : BOOLEAN;
DERIVE
SELF\path.edge̲list : LIST [1:?] OF UNIQUE oriented̲edge
:= conditional̲reverse(SELF.orientation,
SELF.path̲element.edge̲list);
WHERE
WR1: NOT ('TOPOLOGY̲SCHEMA.ORIENTED̲PATH' IN TYPEOF (SELF.path̲element));
END̲ENTITY;
(*
属性定義
path̲element:oriented̲pathを構成するために用いられるエンティティpath。
orientation:ブール型の属性。TRUEの場合,位相上の向きは,path̲elementの向きに一致する。
edge̲list:oriented̲pathを構成するoriented̲edgeのリスト。このリストは,属性orientationを考慮して
path̲elementから導出される。
形式的要件
WR1:path̲elementは,oriented̲pathであってはならない。
5.4.9
open̲path open̲pathは,pathの特殊な下位型とし,pathの通過に当たって各vertexは,1回だけ
現れる。特に,開始vertexと終了vertexとは異なる。open̲pathは,M=1かつGp=0となるグラフなので,
オイラー式(1)は,この場合,次のとおりになる。
(ν−ε)−1=0 ·············································································· (3)
ここで,ν及びεは,それぞれ,pathにおける一意なvertex及びedgeの数とする。特に,pathの位相の属性
は,次の制約を満足しなければならない。
− path中のedgeは一意とする。
(P)[E]=(P){E}
− リスト((P)[E])[V]において,二つのvertexは,ただ1回だけ現れ,その他のvertexは,ちょうど2
回現れる。
− pathのグラフの種数は,0とする。
115
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 式(3)は,次のように解釈される。
|((P)[E]){V}|−|(P){E}|−1=0
EXPRESSによる定義
*)
ENTITY open̲path
SUBTYPE OF (path);
DERIVE
ne : INTEGER := SIZEOF(SELF\path.edge̲list);
WHERE
WR1: (SELF\path.edge̲list[1].edge̲element.edge̲start) :<>:
(SELF\path.edge̲list[ne].edge̲element.edge̲end);
END̲ENTITY;
(*
属性定義
ne:上位型であるpathのedge̲list中の要素数。
形式的要件
WR1:最初のedgeの開始vertexは,最後のedgeの終了vertexに一致してはならない。
非形式的要件
IP1:open̲pathでは,各vertexは,1回だけ現れる。このことは,vertexのリストをedgeデータから構成
する場合,最初及び最後のvertexはリスト中に1回だけ現れ,その他のvertexは2回現れることを意味す
る。
5.4.10 loop loopは,単独のvertex,又は,同一のvertexを始まりかつ終わりとする連結されたedge,
oriented̲edge若しくは直線セグメントを並べることによって構成される位相エンティティとする。loopの
次元数は,0又は1とする。0次元loopの定義域は,単独の点とする。1次元loopの定義域は,連結され
たoriented̲curveとするか,多様体でなくてもよい。loopは,サイクルであるので,その始まりかつ終わ
りの点の配置は,任意とする。loopの定義域は,その境界を含み,かつ0≦Ξ<∞とする。
loopは,単独のvertexによって,oriented̲edgeの順序付けられた集まりによって,又は点の順序付けら
れた集まりによって表現される。
loopはグラフであるので,M及びグラフの種数Glは,グラフ通過アルゴリズムによって決定されるとし
てよい。M=1であるので,オイラー式(1)は,この場合,次のとおりになる。
(ν−εl)−(1−Gl)=0 ······································································ (4)
ここで,ν及びεlは,それぞれ,loop中の一意なvertex及びoriented̲edgeの数とし,Glは,loopの種数と
する。
EXPRESSによる定義
*)
ENTITY loop
SUPERTYPE OF (ONEOF(vertex̲loop, edge̲loop, poly̲loop))
SUBTYPE OF (topological̲representation̲item);
END̲ENTITY;
(*
116
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
非形式的要件
IP1:loopの大きさは,有限とする。vertex̲loopの場合には0となる。
IP2:loopは,開始vertexと終了vertexとが一致する閉(位相)曲線を表す。
5.4.11 vertex̲loop vertex̲loopは,単独のvertexからなる種数0のloopとする。vertexは,vertex̲loop
と独立に存在できる。位相データは,次の制約を満足しなければならない。
− 式(4)(5.4.10参照)を満足しなければならない。
|(L){V}|−1=0
EXPRESSによる定義
*)
ENTITY vertex̲loop
SUBTYPE OF (loop);
loop̲vertex : vertex;
END̲ENTITY;
(*
属性定義
loop̲vertex:loop全体を定義するvertex。
非形式的要件
IP1:vertex̲loopの大きさ及び次元数は,ともに0とする。
IP2:vertex̲loopの種数は,0とする。
5.4.12 edge̲loop edge̲loopは,大きさが0でないloopで,開始vertexと終了vertexが同一のpathとす
る。その定義域は,存在する場合,閉曲線となる。edge̲loopは,自己に重なる部分があってもよい。
EXPRESSによる定義
*)
ENTITY edge̲loop
SUBTYPE OF (loop, path);
DERIVE
ne : INTEGER := SIZEOF(SELF\path.edge̲list);
WHERE
WR1
: (SELF\path.edge̲list[1].edge̲start) :=:
(SELF\path.edge̲1ist[ne].edge̲end);
END̲ENTITY;
(*
属性定義
ne:上位型であるpathのedge̲listの要素数。
形式的要件
WR1:最初のedgeの開始vertexは,最後のedgeの終了vertexと同一でなければならない。これによって
pathが閉じ,loopとなることが保証される。
非形式的要件
IP1:edge̲loopの種数は,1以上でなければならない。
IP2:次のオイラー式[5.4.10の式(4)参照]を満足しなければならない。
117
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(vertexの数)+種数−(edgeの数)=1
IP3:同じedge̲loopによって,同じ向きに2回以上参照されるedgeはない。
5.4.13 poly̲loop poly̲loopは,空間内の平面領域を境界付ける直線edgeをもつloopとする。poly̲loop
は,種数1のloopとする。ここで,loopは,loopのvertexを構成するように順序付けられ,かつ共面な
pointの集まりによって表現される。loopは,その集まりの中で,pointとその後に続くpointとを結ぶ直線
セグメントで構成される。最後のセグメントは,その集まりの最後のpointから最初のpointに向かう。loop
の方向は,直線セグメントの方向となる。エンティティedge̲loopと異なり,poly̲loopのedgeは,polygon
を構成するpointによって暗黙に定義される。
備考 このエンティティは,主に多面体境界表現モデルの効率的なデータ交換を可能にするため
のものである。
poly̲loopは,次の位相上の制約に従わなければならない。
− loopの種数は,1とする。
− 式(4)(5.4.10参照)を満足しなければならない。
|(L){V}|−|(L){El}|=0
EXPRESSによる定義
*)
ENTITY poly̲loop
SUBTYPE OF (loop,geometric̲representation̲item);
polygon : LIST [3:?] OF UNIQUE cartesian̲point;
END̲ENTITY;
(*
属性定義
polygon:loopを定義するpointのリスト。リストの中に重複するpointはない。
非形式的要件
IP1:poly̲loopを定義するpolygon中のすべてのpointは,共面でなければならない。
IP2:poly̲loopの暗黙の稜線は,互いに交差してはならない。暗黙の稜線は,polygon中の連続するpoint
を結ぶ直線とする。
備考 poly̲loopは,暗黙に作られるoriented̲edge及びvertexをもつ。例えば,A及びBがpolygon
リスト中の連続する二つのpointの場合,向きの値がTRUEでvertex̲point Aから
vertex̲point Bへの暗黙なoriented̲edgeが存在する。shellや境界表現のような,より高い水
準のエンティティがedgeの用法に対する検査を要求したとき,例えば,point Bからpoint A
に向かうorientationがTRUEの直線oriented̲edgeと,AからBへ向かうorientationがFALSE
のoriented̲edgeとか等しいと認識できることを仮定する。
5.4.14 face̲bound face̲boundは,faceを境界付けるために用いることを意図したloopとする。
EXPRESSによる定義
*)
ENTITY face̲bound
SUBTYPE OF(topological̲representation̲item);
bound : loop;
orientation : BOOLEAN;
118
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲ENTITY;
(*
属性定義
bound:faceの境界として用いられるloop。
orientation:faceを境界付けるために用いられる場合のloopの向きが,最初に定義されたときと同じであ
るか(TRUF),又は逆であるか(FALSE)のいずれかを示す。orientationがFALSEの場合,faceにおい
て用いられるときには,構成要素のoriented̲edgeの向きは,すべて反転しているとみなす。
5.4.15 face̲outer̲bound face̲outer̲boundは,face̲boundの特殊な下位型であって,faceの外周の境界を
定義するという意味ももつ。faceの二つ以上の境界がface̲outer̲boundとなってはならない。
EXPRESSによる定義
*)
ENTITY face̲outer̲bound
SUBTYPE OF (face̲bound);
END̲ENTITY;
(*
5.4.16 face face(面)は,次元数2の位相エンティティで,直感的には,ループによって境界付けられ
た曲面の一部に対応する。その定義域は,存在する場合,Rmにおいて向き付けられた連結な有限の2-多様
体とし,ハンドルをもたないが,穴をもってもよい。各穴は,loopによって境界付けられる。faceの幾何
の定義域は,存在する場合,faceの境界を含まず,かつ0<Ξ<∞とする。faceは,その境界ループによっ
て表現される。各境界ループは,face̲boundとして定義される。faceは,少なくとも一つの境界をもたな
ければならない。各境界は,互いに異なっていなければならず,更に交差してはならない。場合によって
は,一つのloopが,faceの“外周”loopとして,下位型のface̲outer̲boundを用いて区別されることがあ
る。この場合,faceの定義域を平面内に埋め込む方法が設定され,faceの他の境界ループが外周loopの“内
側”となる。faceの定義域は,弧状連結であるので,いかなる内部loopも,他のloopを内側に含んではな
らない。これは,平面内にどのような埋込みをしようと関係なく,真とする。
幾何のsurfaceかfaceに関連付けられることがある。これは,下位型のface̲surfaceを用いて明示的に行
うか,又は,faceかpoly̲loopで定義される場合には,暗黙に行ってよい。後者の場合,surfaceは,poly̲loop
のpointを含む平面とする。いずれの場合にも,外積n×tがfaceの内部を指すように,位相上の法線nは,
faceに関連付けされる。ここでtは,境界ループの接線とする。すなわち,法線nが上方を指していると
考えた場合,各loopは,faceの上方から見て反時計回りにfaceを回る。各loopには,エンティティface̲bound
を介してブール型のフラグが関連付けされる。ブール型のフラグは,loopの方向がfaceの法線に対して正
しく向き付けされているか(TRUE),又は反転しているか(FALSE)のいずれかを示す。
face̲surfaceであるfaceの場合,位相上の法線nは,基礎となるsurfaceの法線及びブール型の属性
same̲senseから定義される。この位相上の法線から,上に示した外積の規則によって,faceの内部がloop
のどちら側にあるかを決定できる。poly̲loopによって定義されるような暗黙の平面の場合,一意に定まる
曲面の法線が存在しないので,状況が異なる。face及びその境界ループか平面上にあるので,外周loopは,
あいまいさなく求めることができる。faceが有限でなければならないので,faceの内部は,外周loopの内
側に存在し,かつ他のloopの外側に存在する。これらの条件及び指定されたloopの向きによって,位相
上の法線nは,上に示した外積の規則を用いて定義される。与えられたfaceのすべてのpoly̲loopの向き
は,同じnを導かなければならない。
119
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
faceのloopによって参照されるedge及びvertexは,グラフを構成する。このグラフの個々のloopは,
連結構成要素とする。このグラフに関するオイラー式(1)は,次のとおりになる。
(ν−ε)−(L−∑
L
i
li
G
1
)
(
=
)=0 ······························································ (5)
ここで,
li
Gは,i番目のloopのグラフの種数とする。より明確には,次の位相上の制約が満足されなけれ
ばならない。
− loopは,一意とする。
(F){L}=(F)[L]
− リスト((F)[L])[E]中で,個々のedgeは,3回以上は現れない。
− 各oriented̲edgeは,一意とする。
((F)[E]){El}=((F)[L])[El]
− 式(5)は,次を満足しなければならない。
|(((F)[Le]){E}){V}|+|((F)[Lυ]){V}|−|((F)[L]){E}|−|(F)[L]|+ΣGl=0
EXPRESSによる定義
*)
ENTITY face
SUPERTYPE OF (ONEOF(face̲surface, subface, oriented̲face))
SUBTYPE OF (topological̲representation̲item);
bounds : SET[1:?] OF face̲bound;
WHERE
WR1: NOT(mixed̲loop̲type̲set(list̲to̲set(list̲face̲loops(SELF))));
WR2: SIZEOF(QUERY(temp <* bounds | 'TOPOLOGY̲SCHEMA.FACE̲OUTER̲BOUND' IN
TYPEOF(temp))) <= 1;
END̲ENTITY;
(*
属性定義
bounds:faceの境界。これらのうち,たかだか一つがface̲outer̲boundとする。
備考 ある種の閉曲面又は部分閉曲面の場合,一意な外周の境界を求めることはできない。
形式的要件
WR1:faceのloopのいずれかがpoly̲loopである場合,faceのすべてのloopは,poly̲loopでなければなら
ない。
WR2:boundsのうち,たかだか一つがface̲outer̲bound型とする。
非形式的要件
IP1:いかなるedgeも,faceから3回以上参照されない。同一方向では,2回以上参照されない。
IP2:faceの異なるface̲boundは,共通のvertexをもたない。
IP3:幾何が存在する場合,同一face上の異なるloopは,互いに交差してはならない。
IP4:faceは,次のオイラー式[式(5)参照]を満足しなければならない。
(vertexの数)-(edgeの数)-(loopの数)+(loopの種数の和)=0
IP5:boundsの中で参照される各loopは,一意とする。
120
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.4.17 face̲surface face̲surfaceは,faceの下位型とし,その幾何は,関連付けされたsurfaceによって定
義される。faceによって用いられる曲面の部分は,開円盤として平面内に埋込み可能でなければならない。
このときfaceに穴があってもよい。しかし,faceにその境界ループのedge及びvertexとを加えたものは,
平面内に埋込み可能でなくてよい。例えば,球面又は輪環体の全体が覆われる場合である。faceと幾何曲
面との双方で法線の方向を定義しているので、surfaceの法線がfaceの法線の方向に一致するか(TRUE),
又は逆であるか(FALSE)のいずれかを示すために,ブール型のフラグ(向きの属性)が用いられる。face
のloopに含まれるあらゆる構成要素に関連付けされた幾何は,surfaceの幾何と整合しなければならない。
すなわち,すべてのvertex̲point及びedge̲curveの定義域が,faceの幾何であるsurfaceに含まれなければ
ならない。surfaceは,複数のfaceから参照されてもよい。
EXPRESSによる定義
*)
ENTITY face̲surface
SUBTYPE OF(face,geometric̲representation̲item);
face̲geometry
: surface;
same̲sense : BOOLEAN;
END̲ENTITY;
(*
属性定義
face̲geometry:face内部の形状を定義するsurface。このsurfaceは,境界のないものでもよい。faceの定義
域は,このsurface及び継承された属性であるSELF\face.bounds中の境界ループによって定義される。
same̲sense:このフラグは,曲面の法線の向きがfaceの位相上の法線の向きに一致するか(TRUE),又は
逆であるか(FALSE)のいずれかを示す。
非形式的要件
IP1:face̲surfaceの定義域は,そのface̲geometryの定義域をloopによってトリムしたものとして形式的
に定義される。この定義域は,境界ループを含まない。
IP2:face̲surfaceの大きさは,有限かつ0でない。
IP3:face̲surfaceは,多様体とする。
IP4:face̲surfaceは,弧状連結とする。
IP5:face̲surfaceの曲面の種数は,0とする。
IP6:loopは,faceの定義域に含まれない。
IP7:loopの幾何は,faceの幾何と整合しなければならない。これは,face̲surfaceを境界付けるloopを定
義するのに用いられるあらゆるedge̲curve又はvertex̲pointがface̲geometry上になければならないことを
意味する。
IP8:faceのloopは,互いに交差してはならない。
5.4.18 oriented̲face oriented̲faceは,faceの下位型とし,oriented̲faceの向きがface̲elementにおいて定
義されている元の向きに一致するか否かを示す付加的なブール型の向きフラグをもつ。
EXPRESSによる定義
*)
ENTITY oriented̲face
SUBTYPE OF (face);
121
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
face̲element
: face;
orientation : BOOLEAN;
DERIVE
SELF\face.bounds : SET[1:?] OF face̲bound
:= conditional̲reverse(SELF.orientation,SELF.face̲element.bounds);
WHERE
WR1: NOT ('TOPOLOGY̲SCHEMA.ORIENTED̲FACE' IN TYPEOF(SELF.face̲element));
END̲ENTITY;
(*
属性定義
face̲element:このoriented̲faceを構成するために用いられるエンティティface。
orientation:このエンティティの位相上の向きとface̲elementの位相上の向きとの関係。これがTRUEの場
合,位相上の向きはface̲elementの向きに一致する。
bounds:oriented̲faceのboundsは,その方向を反転できるorientationを考慮して,face̲elementのbounds
から導出される。
形式的要件
WR1:face̲elementは,oriented̲faceであってはならない。
5.4.19 subface subfaceは,face又は他のsubfaceの定義域の一部とする。
subfaceに関する位相上の制約は,faceに関するものと同じとする。
EXPRESSによる定義
*)
ENTITY subface
SUBTYPE OF (face);
parent̲face : face;
WHERE
WR1: NOT (mixed̲loop̲type̲set(list̲to̲set(list̲face̲loops(SELF)) +
list̲to̲set(list̲face̲loops(parent̲face))));
END̲ENTITY;
(*
属性定義
parent̲face:SELF\face.boundsによって定義されるsubfaceを含むface(又はsubface)。
形式的要件
WR1:subface中のloopの型は,エンティティparent̲face中のloopの型に一致しなければならない。
非形式的要件
IP1:subfaceの定義域は,parent̲faceの定義域をsubfaceのloopによってトリムしたものとして形式的に
定義される。
IP2:subfaceのすべてのloopは,parent̲faceの定義域とparent̲faceの境界ループの定義域との和に含まれ
なければならない。
5.4.20 connected̲face̲set connected̲face̲setは,face,境界のedge及び境界のvertexの定義域の和が連
結であるようなfaceの集合とする。
122
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
ENTITY connected̲face̲set
SUPERTYPE OF(ONEOF(closed̲she11, open̲shell))
SUBTYPE OF(topological̲representation̲item);
cfs̲faces : SET[1:?] OF face;
END̲ENTITY;
(*
属性定義
cfs̲face:共通のedge又はvertexを介して弧状連結であるfaceの集合。
非形式的要件
IP1:face及びその境界loopの定義域の和は,弧状連結でなければならない。
5.4.21 vertex̲shell vertex̲shellは,単独のvertex̲loopからなるshellとする。vertex̲shell̲extentは,一意
とする。vertex̲loopは,一つのvertex̲shellによってだけ用いられることができる。
vertex̲loopは,vertex̲shellと独立に存在できる。
EXPRESSによる定義
*)
ENTITY vertex̲shell
SUBTYPE OF (topological̲representation̲item);
vertex̲shell̲extent : vertex̲loop;
END̲ENTITY;
(*
属性定義
vertex̲shell̲extent:このshellの大きさを定める単独のvertex̲loop。
非形式的要件
IP1:vertex̲shellの大きさ及び次元数は,ともに0とする。
IP2:vertex̲shellの種数は,0とする。
5.4.22 wire̲shell wire̲shellは,次元数1のshellとする。wire̲shellは,vertex及びedgeから構成される
グラフとみなすことができる。しかし,グラフとしては直接的に表現されず,loopの集合として間接的に
表現される。wire̲shellは,グラフを構成するこれらのloopのvertexとedgeとの和からなる。wire̲shell
の定義域は,存在する場合,通常,多様体でない。
wire̲shellの構造には,次の二つの制限がある。
(a) グラフは,全体として連結でなければならない。
(b) グラフ中の各edgeは,loopの集合からちょうど2回参照されなければならない。
備考1. wire̲shellには,主に二つの応用が考えられる。
2. 任意の連結グラフは,グラフ通過アルゴリズムによって,条件(b)に従う単独のloopとして示
すことができる。このようなグラフは領域の境界となってもよい。
3. closed̲shellのfaceによって参照されるloopの集合は,自動的に条件(b)に従うが,連結であ
る必要はない。しかし,これらのloopが連結グラフ,すなわち,wire̲shellを形成するよう
に,closed̲shellのfaceを分割することは,常に可能とする。したがって,wire̲shellは,
123
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
closed̲shellの“1次元骨格構造”を表現できる。
グラフの種数をGwとし,連結構成要素の数をM=1とすると,グラフのオイラー式(1)は,次のとおりにな
る。
(ν−ε)−(1−Gw)=0 ······································································ (6)
より明確には,次の位相上の制約を満足しなければならない。
− loopは,一意とする。
(Sw){L}=(Sw)[L]
− 各edgeは,二つのloopによって参照されるか,又は単独のloopによって2回参照されなければ
ならない。すなわち,リスト((Sw)[L])[E]中において,各edgeは,ちょうど2回現れる。
|((Sw)[L])[E]|=2|((Sw)[L]){E}|
− 各oriented̲edgeは,一意とする。
((Sw)[L]){El}=((Sw)[L])[El]
− 式(6)を満足しなければならない。
|(((Sw)[L]){E}){V}|-|((Sw)[L]){E}|−1+Gw=0
EXPRESSによる定義
*)
ENTITY wire̲shell
SUBTYPE OF (topological̲representation̲item);
wire̲shell̲extent : SET [1:?] OF loop;
WHERE
WR1: NOT mixed̲loop̲type̲set(wire̲shell̲extent);
END̲ENTITY;
(*
属性定義
wire̲shell̲extent:shellを定義するloopのリスト。
形式的要件
WR1:wire̲shellを構成するloopでは,poly̲loopと他の型のloopとが混在してはならない。
非形式的要件
IP1:wire̲shellの次元数は,1とする。
IP2:wire̲shellの大きさは,有限でかつ0を超える。
IP3:各edgeは,wire̲shell中において,反対の向きにちょうど2回現れる。
IP4:オイラー式を満足しなければならない。
IP5:wire̲shell̲extentを定義するloopは,共通するedge又はvertexを除き,互いに交差しない。
5.4.23 open̲shell open̲shellは,次元数2のshellとする。その定義域は,存在する場合,有限かつ連結
な向き付けされた境界付2-多様体であって,閉曲面でない。それは,一つ以上の穴かその中に存在する
closed̲shellとして考えることかできる。open̲shellの定義域は,0<Ξ<∞とする。open̲shellは,その定義
域がハンドルをもつことができるので,faceに比べて機能的に,より一般的である。
このshellは,face(oriented̲faceであってもよい。)の集まりによって定義される。各faceの向きは,
orientationを考慮すると,次に定義するshellの法線に一致しなけれはならない。orientationは,oriented̲face
のブール型の属性として直接与えることかできる場合,又はshellの要素が属性orientationのないfaceの場
124
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
合には,暗黙によってTRUEとすることができる。
次に示す,open̲shellに関する組合せの制限及びその定義域に関する幾何の制限は,非形式的要件と合
わせて,open̲shellに関連付けされたあらゆる定義域が向き付け可能多様体であることを保証する。
− 各faceへの参照は,一意とする。
− open̲shellは,少なくとも一つのfaceをもつ。
− faceは,複数のopen̲shell中に存在してもよい。
open̲shellの境界は,そのfaceのface̲bound(loop)によって1回だけ参照されるedge及びそれらのedge
のvertexから構成される。open̲shellの定義域は,存在する場合,そのfaceのすべてのedge及びvertexを
含む。
備考 この定義は,faceの定義域の定義と微妙に異なっている。faceの定義域は,その境界を含
まない。例えば,孤立した点又は直線セグメントは,faceの定義域から除かれるが,
open̲shellの定義域からは除かれない(次に示すβを計算するアルゴリズム参照。)。
open̲shellの曲面の種数及び位相上の法線は,その定義域内の穴を埋めて得られるclosed̲shellと同じもの
とする。位相上の法線は,faceのorientationを考慮すると,faceの法線からも導出することができる。
open̲shellは,次のオイラー式を満足する。これは,連結で向き付け可能な曲面に関する最も一般的な形
式のオイラー式とする。
(ν−ε−L+2F)−(2−2H−β)=0 ······················································ (7)
ここで,ν,ε,Ll,及びFは,それぞれ,異なるvertex,edge,face̲bound及びfaceの数とする。Hは曲面
の種数とし,βは穴の数とする。βは,faceの境界を定義するedge及びvertexのグラフから,次の方法によ
って直接求めることができる。
− faceのface̲boundによって2回参照されるすべてのedgeをグラフから削除する。
− edgeと関連付けされていないすべてのvertexを削除する。
− 結果として生じるグラフの種数βを計算する。
曲面の種数Hが既知の場合は,式(7)が成り立つかどうかを確かめられる。通常,曲面の種数は,既知で
ないので,式(7)又はこれと等価な式を用いて種数を計算することになる。Hは,非負の整数であるので,
open̲shellが正当である必要条件として次の不等式が導かれる。
ν−ε−Ll+β=偶数,かつ≦2−2F ··················································· (8)
より明確には,次の位相上の制約を満足しなければならない。
− shellの各faceは,一意とする。
(So){F}=(So)[F]
− shellの各face̲boundは,一意とする。
((So)[F]){Ll}=((So)[F])[Ll]
− shellの各oriented̲edgeは,一意とする。
(((So)[F])[Ll]){E}=(((So)[F])[Ll])[El]
− リスト(((So)[F])[Ll])[El]中で,1回だけ現れるedgeが少なくとも一つ存在し,3回以上現れるedge
は存在しない。1回だけ現れるedgeは,shellの境界上に存在する。
− オイラー条件(8)及び式(7)を満足しなければならない。
|((((So)[F]){elL}){E}){V}|+|(((So)[F]){vlL}){V}|−|(((So)[F]){Ll}){E}|
−|((So)[F])[Ll]|+B=偶数,かつ≦2−2|(So)[F]|
2−2H−B=|((((So)[F]){elL}){E}){V}|+|(((So)[F]){vlL}){V}|
125
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−|(((So)[F]){Ll}){E}|−|((So)[F])[Ll]|+2|(So)[F]
EXPRESSによる定義
*)
ENTITY open̲shell
SUBTYPE OF (connected̲face̲set);
END̲ENTITY;
(*
属性定義
SELF\connected̲face̲set.cfs̲faces:oriented̲faceを含んでもよいfaceの集合であって,open̲shellを構成
する。
非形式的要件
IP1:いかなるedgeも,faceのloopから少なくとも1回は参照されるが,3回以上は参照されない。
IP2:各oriented̲edgeの参照は,一意とする。
IP3:いかなるedgeも,三つ以上のfaceから参照されてはならない。
IP4:shellの異なるfaceは,互いに交差しないか,edge又はvertexを共有してもよい。
IP5:異なるedgeは,互いに交差しないが,vertexを共有してもよい。
IP6:オイラー式を満足しなければならない。
IP7:open̲shellは,向き付けされた弧状連結である2-多様体でなければならない。
IP8:open̲shellは,少なくとも一つの穴をもつ。
IP9:open̲shellの各faceへの位相上の法線は,open̲shellの位相上の法線と矛盾してはならない。
5.4.24 oriented̲open̲shell oriented̲open̲shellは,別のopen̲shellから構成されるopen̲shellであって,
構成されたopen̲shellの向きが元のopen̲shellの向きに一致するか否かを示すブール型の向きフラグをも
つ。向きを除けば,oriented̲open̲shellは,元のopen̲shellと等価とする。
EXPRESSによる定義
*)
ENTITY oriented̲open̲shell
SUBTYPE OF (open̲shell);
open̲shell̲element : open̲shell;
orientation : BOOLEAN;
DERIVE
SELF\connected̲face̲set.cfs̲faces : SET [1:?] OF face
:= conditional̲reverse(SELF.orientation,
SELF.open̲shell̲element.cfs̲faces);
WHERE
WR1: NOT ('TOPOLOGY̲SCHEMA.ORIENTED̲OPEN̲SHELL'
IN TYPEOF (SELF.open̲shell̲element));
END̲ENTITY;
(*
属性定義
open̲shell̲element:oriented̲open̲shellのfaceを定義するopen̲shell。
126
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
orientation:定義されるoriented̲open̲shellの向きと,参照されるopen̲shell̲elementの向きとの関係。
cfs̲faces:oriented̲open̲shellのfaceの集合。open̲shell̲elementのfaceから,場合によっては向きを反転
することで得られる。
形式的要件
WR1:open̲shell̲elementの型は,oriented̲open̲shellであってはならない。
5.4.25 closed̲shell closed̲shellは,次元数2のshellであって,通常R3における領域の境界として用いら
れる。closed̲shellは境界をもたず,大きさは有限かつ0でない。このshellが座標空間R3中で定義域をも
つ場合,空間は二分され,一方が有限の連結領域となり,他方が無限の連結領域となる。この場合,shell
の位相上の法線は,有限の領域から無限の領域の向きに定義される。
このshellは,faceの集まりとして定義される。このときfaceは,oriented̲faceであってもよい。orientation
を考慮すると,各faceの向きは,上で定義したshellの法線に一致しなければならない。orientationは,
oriented̲faceのブール型の属性として直接与えるか,又はshellの要素が属性orientationのないfaceの場合
には暗黙によってTRUEとするか,のいずれかとする。
closed̲shellに関する組合せの制限及びその定義域に関する幾何の制限は,closed̲shellに関連付けされた
あらゆる定義域が向き付け可能閉多様体であることを保証する。closed̲shellの定義域は,存在する場合,
向き付けされた連結閉2-多様体とする。これは,種数H(ただしH≧0)の輪環体と位相的に等価である。
Hは,shellの曲面の種数として参照される。種数Hのshellが座標空間R3中に定義域をもつ場合,その内
部の有限な領域は,H個の貫通穴をあけた球と位相的に等価になる。
この場合,穴はないので,曲面オイラー式(7)でβ=0とできる。open̲shellの場合と同様に,曲面の種数H
は,既知でなくてもよいが,0以上の整数でなければならない。したがって,正当なclosed̲shellの必要条
件(十分条件でない)は,次のとおりとなる。
ν−ε−Ll=偶数,かつ≦2−2F ······················································· (9)
より明確には,次の位相上の制約を満足しなければならない。
− shellの各faceは,一意とする。
(Sc){F}=(Sc)[F]
− shellの各face̲boundは,一意とする。
((Sc)[F]){Ll}=((Sc)[F])[Ll]
− shellの各oriented̲edgeは,一意とする。
(((Sc)[F])[Ll]){El}=(((Sc)[F])[Ll])[El]
− shellの各edgeは,ちょうど二つのface̲boundに使われるか,又は一つのface̲boundに2回使わ
れる。
|(((Sc)[F])[Ll]){El}|=2|(((Sc)[F])[Ll]){E}|
すなわち,リスト(((Sc)[F])[Ll])[E]中で,各edgeは,ちょうど2回現れる。
− オイラーの条件(9),場合によっては式(7)を満足しなければならない。
2−2H=|((((Sc)[F]){elL}){E}){V}|+|(((Sc)[F]){vlL}){V}|
−|(((Sc)[F]){Ll}){E}|−|((Sc)[F])[Ll]|+2|(Sc)[F]|
|((((Sc)[F]){elL}){E)}){V}|+|(((Sc)[F]){vlL}){V}|−|(((Sc)[F]){Ll}){E}|
−|((Sc)[F])[Ll]|=は偶数,かつ≦2−2|(Sc)[F]|
EXPRESSによる定義
*)
127
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ENTITY closed̲shell
SUBTYPE OF (connected̲face̲set);
END̲ENTITY;
(*
属性定義
SELF\connected̲face̲set.cfs̲faces:closed̲shellを定義するface(oriented̲faceを含む。)の集合。
非形式的要件
IP1:あらゆるedgeは,faceに属するloopからちょうど2回参照される。
IP2:各oriented̲edgeの参照は,一意とする。
IP3:いかなるedgeも三つ以上のfaceから参照されてはならない。
IP4:shellの異なるfaceは,互いに交差しないか,edge又はvertexを共有してもよい。
IP5:異なるedgeは,互いに交差しないが,vertexを共有してもよい。
IP6:各faceの参照は,一意とする。
IP7:shellのloopには,poly̲loopと他の種類のloopとが混在してはならない。
IP8:closed̲shellは,向き付けされた弧状連結である多様体でなければならない。
IP9:オイラー式を満足しなければならない。
IP10:closed̲shellの各faceへの位相上の法線は,closed̲shellへの位相上の法線と矛盾してはならない。
これは,各faceへの位相上の法線が存在する場合,orientationを考慮すると,closed̲shellによって境界付
けられる有限の領域から外側の無限の領域を向くことを意味する。
5.4.26 oriented̲closed̲shell oriented̲closed̲shellは,別のclosed̲shellから構成されるclosed̲shellであっ
て,構成されたclosed̲shellの向きが元のclosed̲shellの向きに一致するか否かを示すブール型の向きフラ
グをもつ。
oriented̲closed̲shellは,元のclosed̲shellと等価とするが,向きが反対であってもよい。
EXPRESSによる定義
*)
ENTITY oriented̲closed̲shell
SUBTYPE OF (closed̲shell);
closed̲shell̲element
: closed̲shell;
orientation : BOOLEAN;
DERIVE
SELF\connected̲face̲set.cfs̲faces : SET [1:?] OF face
:=conditional̲reverse(SELF.orientation,
SELF.closed̲shell̲element.cfs̲faces);
WHERE
WR1: NOT ('TOPOLOGY̲SCHEMA.ORIENTED̲CLOSED̲SHELL'
INTYPE OF (SELF.closed̲shell̲element));
END̲ENTITY;
(*
属性定義
closed̲shell̲element:oriented̲closed̲shellのfaceを定義するclosed̲shell。
128
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
orientation:定義されるoriented̲closed̲shellの向きと,参照されるclosed̲shell̲elementの向きとの関係。
cfs̲faces:oriented̲closed̲shellのfaceの集合。closed̲shell̲elementのfaceから,場合によっては向きを反
転することによって得られる。
形式的要件
WR1:closed̲shell̲elementの型は,oriented̲closed̲shellであってはならない。
5.4.27 connected̲edge̲set connected̲edge̲setは,edge及び境界vertexの定義域の和が弧状連結であるよ
うなedgeの集合とする。
EXPRESSによる定義
*)
ENTITY connected̲edge̲set
SUBTYPE OF (topological̲representation̲item);
ces̲edges : SET [1:?] OF edge;
END̲ENTITY;
(*
属性定義
ces̲edges:共通のvertexで結合された弧状連結であるedgeの集合。
非形式的要件
IP1:connected̲edge̲setの次元数は,1とする。
IP2:connected̲edge̲setのedgeの定義域は,互いに交差してはならない。
5.5
topology̲schemaの関数定義
5.5.1
conditional̲reverse この関数は,最初の引数に応じて入力された位相そのままか,又はその向き
を逆にした位相の複写を返す。
EXPRESSによる定義
*)
FUNCTION conditional̲reverse (p
: BOOLEAN;
an̲item
: reversible̲topology)
: reversible̲topology;
IF p THEN
RETURN (an̲item);
ELSE
RETURN (topology̲reversed (an̲item));
END̲IF;
END̲FUNCTION;
(*
引数定義
p:(入力)向きの反転が必要かどうかを示すブール値。
an̲item:(入力)必要ならば反転可能な要素。
5.5.2
topology̲reversed この関数は,向きが反転されている以外,入力された位相と等価な位相を返す。
EXPRESSによる定義
*)
129
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
FUNCTION topology̲reversed (an̲item : reversible̲topology)
: reversible̲topology;
IF ('TOPOLOGY̲SCHEMA.EDGE' IN TYPEOF (an̲item)) THEN
RETURN (edge̲reversed (an̲item));
END̲IF;
IF ('TOPOLOGY̲SCHEMA.PATH' IN TYPEOF (an̲item)) THEN
RETURN (path̲reversed (an̲item));
END̲IF;
IF ('TOPOLOGY̲SCHEMA.FACE̲BOUND' IN TYPEOF (an̲item)) THEN
RETURN (face̲bound̲reversed (an̲item));
END̲IF;
IF ('TOPOLOGY̲SCHEMA.FACE' IN TYPEOF (an̲item)) THEN
RETURN (face̲reversed (an̲item));
END̲IF;
IF ('TOPOLOGY̲SCHEMA.SHELL' IN TYPEOF (an̲item)) THEN
RETURN (shell̲reversed (an̲item));
END̲IF;
IF ('SET'IN TYPEOF (an̲item))THEN
RETURN (set̲of̲topology̲reversed (an̲item));
END̲IF;
IF ('LIST' IN TYPEOF (an̲item)) THEN
RETURN (list̲of̲topology̲reversed (an̲item));
END̲IF;
RETURN (?);
END̲FUNCTION;
(*
引数定義
an̲item:(入力)向きが逆にされる反転可能な位相要素。
戻り値:(出力)an̲itemの向きを反転させた結果のtopological̲representation̲item。
5.5.3
edge̲reversed この関数は,向きが反転されている以外,入力されたedgeと等価なedgeを返す。
EXPRESSによる定義
*)
FUNCTION edge̲reversed (an̲edge:edge) : edge;
LOCAL
the̲reverse : edge;
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.ORIENTED̲EDGE' IN TYPEOF (an̲edge)) THEN
the̲reverse := oriented̲edge (an̲edge\oriented̲edge.edge̲element,
(NOT (an̲edge\oriented̲edge.orientation)));
ELSE
130
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
the̲reverse := oriented̲edge (an̲edge, FALSE);
END̲IF;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
an̲edge:(入力)向きが逆にされるedge。
the̲reverse:(出力)向きを反転した結果。
5.5.4
path̲reversed この関数は,向きが反転されている以外,入力されたpathと等価なpathを返す。
EXPRESSによる定義
*)
FUNCTION path̲reversed (a̲path : path) : path;
LOCAL
the̲reverse : path;
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.ORIENTED̲PATH' IN TYPEOF (a-path)) THEN
the̲reverse := oriented̲path(a̲path\oriented̲path.path̲element,
(NOT(a̲path\oriented̲path.orientation)));
ELSE
the̲reverse := oriented̲path (a̲path, FALSE);
END̲IF;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲path:(入力)向きが逆にされるpath。
the̲reverse:(出力)向きを反転した結果。
5.5.5
face̲bound̲reversed この関数は,向きが反転されている以外,入力されたface̲boundと等価な
face̲boundを返す。
EXPRESSによる定義
*)
FUNCTION face̲bound̲reversed (a̲face̲bound : face̲bound) : face̲bound;
LOCAL
the̲reverse : face̲bound;
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.FACE̲OUTER̲BOUND' IN TYPEOF (a̲face̲bound)) THEN
the̲reverse := face̲bound (a̲face̲bound\face̲bound.bound,
(NOT (a̲face̲bound\face̲bound.orientation)));
ELSE
the̲reverse := face̲bound (a̲face̲bound.bound,
131
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(NOT (a̲face̲bound.orientation)));
END̲IF;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲face̲bound:(入力)向きが逆にされるface̲bound。
the̲reverse:(出力)向きを反転した結果。
5.5.6
face̲reversed この関数は,向きが反転されている以外,入力されたfaceと等価なfaceを返す。
EXPRESSによる定義
*)
FUNCTION face̲reversed (a̲face : face) : face;
LOCAL
the̲reverse : face;
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.ORIENTED̲FACE' IN TYPEOF (a̲face)) THEN
the̲reverse := oriented̲face (a̲face\oriented̲face.face̲element,
(NOT (a̲face\oriented̲face.orientation)));
ELSE
the̲reverse := oriented̲face (a̲face, FALSE);
END̲IF;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲face:(入力)向きが逆にされるface。
the̲reverse:(出力)向きを反転した結果。
5.5.7
shell̲reversed この関数は,向きが反転されている以外,入力されたshellと等価なshellを返す。
EXPRESSによる定義
*)
FUNCTION shell̲reversed (a̲shell : shell) : shell;
LOCAL
the̲reverse : shell;
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.ORIENTED̲OPEN̲SHELL' IN TYPEOF (a̲shell)) THEN
the̲reverse := oriented̲open̲shell(
a̲shell\oriented̲open̲shell.open̲shell̲element,
(NOT (a̲shell\oriented̲open̲shell.orientation)));
ELSE
IF ('TOPOLOGY̲SCHEMA.OPEN̲SHELL' IN TYPEOF (a-shell)) THEN
132
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
the̲reverse := oriented̲open̲shell(a̲shell, FALSE);
ELSE
IF ('TOPOLOGY̲SCHEMA.ORIENTED̲CLOSED̲SHELL' IN TYPEOF (a̲shell)) THEN
the̲reverse := oriented̲closed̲shell(
a̲shell\oriented̲closed̲shell.closed̲shell̲element,
NOT (a̲shell\oriented̲closed̲shell.orientation));
ELSE
IF ('TOPOLOGY̲SCHEMA.CLOSED̲SHELL' IN TYPEOF (a̲shell)) THEN
the̲reverse := oriented̲closed̲shell (a̲shell, FALSE);
ELSE
the̲reverse := ?;
END̲IF;
END̲IF;
END̲IF;
END̲IF;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲shell:(入力)向きが逆にされるshell。
the̲reverse:(出力)向きを反転した結果。
5.5.8
set̲of̲topology̲reversed この関数は,各要素の向きが反転されている以外,入力された位相の集
合と等価な位相の集合を返す。
EXPRESSによる定義
*)
FUNCTION set̲of̲topology̲reversed (a̲set : set̲of̲reversible̲topology̲item)
: set̲of̲reversible̲topology̲item;
LOCAL
the̲reverse : set̲of̲reversible̲topology̲item;
END̲LOCAL;
the̲reverse := [ ];
REPEAT i := 1 TO SIZEOF (a̲set);
the̲reverse := the̲reverse + topology̲reversed (a̲set [i]);
END̲REPEAT;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲set:(入力)向きが逆にされる位相要素の集合。
the̲reverse:(出力)向きを反転した結果。
133
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.5.9
list̲of̲topology̲reversed この関数は,リストの各要素の向きが反転されていて,更にそのリスト
内の要素の順番が逆であること以外は,入力された位相のリストと等価な位相のリストを返す。
EXPRESSによる定義
*)
FUNCTION list̲of̲topology̲reversed (a̲list
: list̲of̲reversible̲topology̲item)
: list̲of̲reversible̲topology̲item;
LOCAL
the̲reverse : list̲of̲reversible̲topology̲item;
END̲LOCAL;
the̲reverse := [ ];
REPEAT i := 1 TO SIZEOF (a̲list);
the̲reverse := topology̲reversed (a̲list [i]) + the̲reverse;
END̲REPEAT;
RETURN (the̲reverse);
END̲FUNCTION;
(*
引数定義
a̲list:(入力)向き及びリストの順番が逆にされる位相要素のリスト。
the̲reverse:(出力)向き及び順番を反転した結果。
5.5.10 boolean̲choose この関数は,ブール型の入力引数の値に応じて二つの選択のうちの一つを返す。
この二つの選択も,入力引数とする。
EXPRESSによる定義
*)
FUNCTION boolean̲choose (b : BOOLEAN;
choice1, choice2 : GENERIC) : GENERIC;
IF b THEN
RETURN(choice1);
ELSE
RETURN(choice2);
END̲IF;
END̲FUNCTION;
(*
引数定義
b:(入力)要素がchpice1(TRUE)であるかchoice2(FALSE)であるかを選択するために使用されるブ
ール値。
choice1:(入力)選択対象の1番目の要素。
choice2:(入力)選択対象の2番目の要素。
5.5.11 path̲head̲to̲tail この関数は,入力pathのedgeについて,それぞれのedgeの終了vertexが,そ
れに続くedgeの開始vertexと同じ場合,TRUEを返す。
134
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
FUNCTION path̲head̲to̲tail(a̲path : path) : LOGICAL;
LOCAL
n : INTEGER;
p : LOGICAL :=TRUE;
END̲LOCAL;
n := SIZEOF (a̲path.edge̲list);
REPEAT i := 2 TO n;
p := p AND (a̲path.edge̲list [i-1].edge̲end :=:
a̲path.edge̲list [i].edge̲start);
END̲REPEAT;
RETURN (p);
END̲FUNCTION;
(*
引数定義
a̲path:(入力)構成要素のedgeについて,その終点と次のedgeの始点とが一致するように接続されてい
るかどうかが検査されるpath。
p:(出力)path内のすべてのedgeについて,その終点と次のedgeの始点とが一致するように接続されて
いればTRUEとなる論理型の変数。
5.5.12 list̲face̲loops この関数は,与えられたface(又はsubface)に対し,face又はsubface内のloop
のリストを返す。
EXPRESSによる定義
*)
FUNCTION list̲face̲loops(f : face) : LIST [0:?] OF loop;
LOCAL
loops : LIST [0:?] OF loop := [];
END̲LOCAL;
REPEAT i := 1 TO SIZEOF (f.bounds);
loops := loops + (f.bounds [i].bound);
END̲REPEAT;
RETURN(loops);
END̲FUNCTION;
(*
引数定義
f:(入力)境界loopのリストを作ることが必要なface。
loops:(出力)fのloopのリスト。
5.5.13 list̲loop̲edges この関数は,与えられたloopに対し,そのloop内のedgeのリストを返す。
EXPRESSによる定義
*)
135
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
FUNCTION list̲looP̲edges(l: loop): LIST[0:?] OF edge;
LOCAL
edges : LIST [0:?] OF edge :=[];
END̲LOCAL;
IF 'TOPOLOGY̲SCHEMA.EDGE̲LOOP' IN TYPEOF(l) THEN
REPEAT i := 1 TO SIZEOF(l\path.edge̲list);
edges := edges + (l\path.edge̲list [i].edge̲element);
END̲REPEAT;
END̲IF;
RETURN(edges);
END̲FUNCTION;
(*
引数定義
l:(入力)edgeのリストを作ることが必要なloop。
edges:(出力)lのedgeのリスト。
5.5.14 list̲shell̲edges この関数は,与えられたshellに対し,そのshell内のedgeのリストを返す。
EXPRESSによる定義
*)
FUNCTION list̲shell̲edges(s : shell) : LIST [0:?] OF edge;
LOCAL
edges : LIST [0:?] OF edge := [];
END̲LOCAL;
REPEAT i := 1 TO SIZEOF(list̲shell̲loops(s));
edges := edges + list̲loop̲edges(list̲shell̲loops(s)[i]);
END̲REPEAT;
RETURN(edges);
END̲FUNCTION;
(*
引数定義
s:(入力)edgeのリストを作ることが必要なshell。
edges:(出力)sのedgeのリスト。
5.5.15 list̲shell̲faces この関数は,与えられたshellに対し,そのshell内のfaceのリストを返す。
EXPRESSによる定義
*)
FUNCTION list̲shell̲faces(s : shell) : LIST [0:?] OF face;
LOCAL
faces : LIST [0:?] OF face := [];
END̲LOCAL;
IF ('TOPOLOGY̲SCHEMA.CLOSED̲SHELL' IN TYPEOF(s)) OR
('TOPOLOGY̲SCHEMA.OPEN̲SHELL' IN TYPEOF(s)) THEN
136
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
REPEAT i := 1 TO SIZEOF(s\connected̲face̲set.cfs̲faces);
faces := faces + s\connected̲face̲set.cfs̲faces[i];
END̲REPEAT;
END̲IF;
RETURN(faces);
END̲FUNCTION;
(*
引数定義
s:(入力)faceのリストを作ることが必要なshell。
faces:(出力)sのfaceのリスト。
5.5.16 list̲shell̲loops この関数は,与えられたshellに対し,そのshell内のlooPのリストを返す。
EXPRESSによる定義
*)
FUNCTION list̲shell̲loops(s : shell) : LIST [0:?] OF loop;
LOCAL
loops : LIST [0:?] OF loop := [];
END̲LOCAL;
IF 'TOPOLOGY̲SCHEMA.VERTEX̲SHELL' IN TYPEOF(s) THEN
loops := loops + s.vertex̲shell̲extent;
END̲IF;
IF 'TOPOLOGY̲SCHEMA.WIRE̲SHELL' IN TYPEOF(s) THEN
REPEAT i := 1 TO SIZEOF(s.wire̲shell̲extent);
loops := loops + s.wire̲shell̲extent[i];
END̲REPEAT;
END̲IF;
IF ('TOPOLOGY̲SCHEMA.OPEN̲SHELL' IN TYPEOF(s)) OR
('TOPOLOGY̲SCHEMA.CLOSED̲SHELL' IN TYPEOF(s)) THEN
REPEAT i := 1 TO SIZEOF(s.cfs̲faces);
loops := loops + list̲face̲loops(s.cfs̲faces[i]);
END̲REPEAT;
END̲IF;
RETURN(loops);
END̲FUNCTION;
(*
引数定義
s:(入力)loopのリストを作ることが必要なshell。
loops:(出力)sのloopのリスト。
5.5.17 mixed̲loop̲type̲set この関数は,loopの集合に対して,その集合がpoly̲loopと他の型のloop
(edge̲loop又はvertex̲loop)との両者を含む場合,TRUEを返す。
EXPRESSによる定義
137
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
FUNCTION mixed̲loop̲type̲set(l: SET[0:?] OF loop):LOGICAL;
LOCAL
i : INTEGER;
poly̲loop̲type
: LOGICAL;
END̲LOCAL;
IF (SIZEOF(1) <=1) THEN
RETURN(FALSE);
END̲IF;
poly̲loop̲type := ('TOPOLOGY̲SCHEMA.POLY̲LOOP' IN TYPEOF(l[1]));
REPEAT i := 2 TO SIZEOF(l);
IF(('TOPOLOGY̲SCHEMA.POLY̲LOOP'IN TYPEOF(l[i])) <> poly̲loop̲type) THEN
RETURN(TRUE);
END̲IF;
END̲REPEAT;
RETURN(FALSE);
END̲FUNCTION;
(*
引数定義
l:(入力)poly̲loopと他の型のloopとの混合であるかどうかを,決定することが必要なloopの集合。
5.5.18 list̲to̲set この関数は,LISTからSETを生成する。そのSETの要素の型は,元のLISTの型と同
じとする。
EXPRESSによる定義
*)
FUNCTION list̲to̲set(l : LIST [0:?] OF GENERIC: T) : SET OF GENERIC:T;
LOCAL
s : SET OF GENERIC:T := [ ];
END̲LOCAL;
REPEAT i := 1 TO SIZEOF(l);
s := s + l[i];
END̲REPEAT;
RETURN(s);
END̲FUNCTION;
(*
引数定義
l:(入力)SETに変換されるべき要素のLIST。
s:(出力)lに対応するSET。
5.5.19 edge̲curve̲pcurves この関数は,edge̲curveに関連付けられている(すなわち,その幾何を表現
している)pcurveの集合を返す。
EXPRESSによる定義
138
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*)
FUNCTION edge̲curve̲pcurves (an̲edge : edge̲curve;
the̲surface̲curves:SETOFsurface̲curve)
: SET OF pcurve;
LOCAL
a̲curve : curve;
result : SET OF pcurve;
the̲geometry
: LIST[1:2] OF pcurve̲or̲surface;
END̲LOCAL;
a̲curve := an̲edge.edge̲geometry;
result := [];
IF 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(a̲curve) THEN
result := result + a̲curve;
ELSE
IF 'GEOMETRY̲SCHEMA.SURFACE̲CURVE' IN TYPEOF(a̲curve) THEN
the̲geometry := a̲curve\surface̲curve.associated̲geometry;
REPEAT k := 1 TO SIZEOF(the̲geometry);
IF 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF (the̲geometry[k])
THEN
result := result + the̲geometry[k];
END̲IF;
END̲REPEAT;
ELSE
REPEAT j := 1 TO SIZEOF(the̲surface̲curves);
the̲geometry := the̲surface̲curves[j].associated̲geometry;
IF the̲surface̲curves[j].curve̲3d :=: a̲curve
THEN
REPEAT k := 1 TO SIZEOF(the̲geometry);
IF 'GEOMETRY̲SCHEMA.PCURVE' IN TYPEOF(the̲geometry[k])
THEN
result := result + the̲geometry[k];
END̲IF;
END̲REPEAT;
END̲IF;
END̲REPEAT;
END̲IF;
END̲IF;
RETURN(RESULT);
END̲FUNCTION;
(*
139
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
引数定義
an̲edge:(入力)探索すべきpcurveを結合しているedge̲curve。
the̲surface̲curves:(入力)pcurveの探索の対象となるすべてのsurface̲curveの集合。
result:(出力)an̲edgeに関連付けられているすべてのpcurveの集合。
5.5.20 vertex̲point̲pcurves この関数は,vertex̲pointに関連付けられている(すなわち,その幾何を表
現している)pcurveの集合を返す。
EXPRESSによる定義
*)
FUNCTION vertex̲point̲pcurves (a̲vertex : vertex̲point;
the̲degenerates : SET OF evaluated̲degenerate̲pcurve)
: SET OF degenerate̲pcurve;
LOCAL
a̲point : point;
result : SET OF degenerate̲pcurve;
END̲LOCAL;
a̲point := a̲vertex.vertex̲geometry;
result := [];
IF 'GEOMETRY̲SCHEMA.DEGENERATE̲PCURVE' IN TYPEOF (a̲point) THEN
result := result + a̲point;
ELSE
REPEAT j := 1 TO SIZEOF(the̲degenerates);
IF (the̲degenerates[j].equivalent̲point :=: a̲point) THEN
result := result + the̲degenerates[j];
END̲IF;
END̲REPEAT;
END̲IF;
RETURN(RESULT);
END̲FUNCTION;
(*
引数定義
a̲vertex:(入力)探索すべきpcurveを結合しているvertex̲point。
the̲degenerates: (入力)pcurveの探索の対象となるすべてのevaluated̲degenerate̲pcurveの集合。
result:(出力)a̲vertexと同じ幾何をもっているすべてのdegenerate̲pcurveの集合。
EXPRESSによる定義
*)
END̲SCHEMA; -- topology̲schema の終了
(*
6. 形状モデル (Geometric model) 次のEXPRESS宣言は,geometric̲model̲schemaを開始し,必要な外
部参照を明らかにする。
140
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
SCHEMA geometric̲model̲schema;
REFERENCE FROM geometry̲schema;
REFERENCE FROM topology̲schema;
REFERENCE FROM measure̲schema(length̲measure,
positive̲length̲measure,
plane̲angle̲measure,
plane̲angle̲unit,
positive̲plane̲angle̲measure);
(*
備考1. 上で参照しているスキーマは,次の規格による。
geometry̲schema この規格の4.
topology̲schema この規格の5.
measure̲schema JIS B 3700-41
2. このスキーマの図式表現を附属書Dの図D.16〜D.18に示す。
6.1
概要 geometric̲model̲schemaは,オブジェクトの大きさ,位置及び形状を記述するデータの交換に
必要な基本的なリソースの集合を扱う。solid̲modelの下位型は,3次元立体オブジェクトの正確な大きさ
及び形状を記述するデータの交換に必要な,基本的なリソースを与える。ここでは,CSG(Constructive Solid
Geometry)及び境界表現(Boundary Representation, B-rep)という,2種類の古典的な立体モデルを含む。
ここでは,CSG又は境界表現のモデルに比べて,幾何的に及び位相的に情報の完全性が低いエンティティ
を含む。これらのエンティティは,立体モデリングシステムとは異なるシステム間でのデータ交換に適し
ている。
このスキーマでは,エンティティを上位型solid̲model及びその種々の下位型を先頭に,論理的な順番で
規定する。これらの下位型は,種々の境界表現とCSG立体とを含む。solid̲modelの下位型の後に,曲面
モデル,ワイヤフレームモデル及び幾何データ集合のエンティティが続く。
6.2
基本概念及び前提条件 CSGモデルは,構成要素の基本立体及びモデルの構成に用いられるブール
操作[union(和),intersection(積)又はdifference(差)]の並びによって表現する。標準的なCSG基本立
体は,cone,cylinder,sphere,torus,block及びright̲angular̲wedgeとし,その最終的な位置及び向きにお
いて定義されることが望ましい。ブール操作の論理的な並びを表すエンティティは,1個の演算子及び2
個の演算項をもつboolean̲resultとする。ブール操作の結果を演算項とすることによって,入れ子の演算を
可能とする。CSG基本立体のほかに,solid̲model(掃引立体及びhalf̲space̲solidを含む。)をブール演算
項としてもよい。掃引立体は,swept̲face̲solid及びswept̲area̲solidとする。掃引立体を得るには,平面
(穴を含んでもよい。)を立上げ又は回転する。half̲space̲solidは,基本的には,曲面の方の側にある半無
限の立体として定義する。これをbox̲domainで有限にしてもよい。
境界表現モデルは,その外部又は内部の境界を定義するシェルの集合で表現する。関連する幾何の定義
が適切であることと,モデル中の頂点,稜線,面,ループ及びシェルの個数に関するオイラー式を満足す
ることとを,制約によって保証する。faceted̲brepは,すべての面が平面の場合及び各loopかpoly̲loopの
場合の境界表現に限定する。
エンティティsolid̲replicaは,既に存在する立体の複製を新しい配置に生成する機構をもつ。
141
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
shell̲based̲surface̲model
,
face̲based̲surface̲model
,
shell̲based̲wireframe̲model
,
edge̲based̲wireframe̲model,geometric̲set及びgeometric̲curve̲setのエンティティは,manifold̲solid̲brep
としての整合性検査を行わなくてよい。これらは,不完全なモデル又は非多様体オブジェクト(2次元モ
デルを含む。)のデータ交換に用いることができる。
6.3
geometric̲model̲schemaの型定義
6.3.1
boolean̲operand この選択型boolean̲operand(ブール演算項)は,CSG立体を作るブール操作が
適用可能なすべての型のエンティティを明らかにする。
EXPRESSによる定義
*)
TYPE boolean̲operand = SELECT
(solid̲model,
half̲space̲solid,
csg̲primitive,
boolean̲result);
END̲TYPE;
(*
6.3.2
boolean̲operator この列挙型boolean̲operator(ブール演算子)は,CSG立体の定義に用いられる
3種類のブール演算子を定義する。
EXPRESSによる定義
*)
TYPE boolean̲operator = ENUMERATION OF
(union,
intersection,
difference);
END̲TYPE;
(*
列挙項目の定義
union:2個の立体が定義する空間領域の,正規化された集合論的な和を構成する演算。
intersection:2個の立体が定義する空間領域の,正規化された集合論的な積を構成する演算。
difference:2個の立体が定義する空間領域の,正規化された集合論的な差を構成する演算。
6.3.3
csg̲primitive この選択型csg̲primitive(CSG基本立体)は,ブール操作か適用可能なCSG基本
立体の集合を定義する。CSG基本立体は,sphere,right̲circular̲cone,right̲circular̲cylinder,torus,block
及びright̲angular̲wedgeとする。
EXPRESSによる定義
*)
TYPE csg̲primitive = SELECT
(sphere,
block,
right̲angular̲wedge,
torus,
142
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
right̲circular̲cone,
right̲circular̲cylinder);
END̲TYPE;
(*
6.3.4
csg̲select この選択型は,CSG立体の木の根として選択可能なエンティティの型(CSG基本立体
が1個だけという特別な場合も含む。)を明らかにする。
EXPRESSによる定義
*)
TYPE csg̲select = SELECT
(boolean̲result,
csg̲primitive);
END̲TYPE;
(*
6.3.5
geometric̲set̲select この選択型は,geometric̲setに存在可能なエンティティの型を明らかにする。
EXPRESSによる定義
*)
TYPE geometric̲set̲select = SELECT
(point,
curve,
surface);
END̲TYPE;
(*
6.3.6
surface̲model この選択型は,曲面モデルのすべてのエンティティの型を明らかにする。
製品モデルの表現の幾つかは,曲面の集まりからなるが,それが立体の完全な境界を作るとは限らない。
これらは,face又はshellの集まりで表現できる。
EXPRESSによる定義
*)
TYPE surface̲model = SELECT
(shell̲based̲surface̲model,
face̲based̲surface̲model);
END̲TYPE;
(*
6.3.7
wireframe̲model この選択型は,ワイヤフレームモデルのすべてのエンティティの型を明らかに
する。
形状モデルのワイヤフレーム表現は,モデルの境界を作る曲面の交差についての情報だけを含むが,曲
面それ自身についての情報を含まない。
EXPRIESSによる定義
*)
TYPE wireframe̲model = SELECT
(shell̲based̲wireframe̲model,
143
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
edge̲based̲wireframe̲model);
END̲TYPE;
(*
6.4
geometric̲model̲schemaのエンティティ定義 ここで扱うエンティティは,geometric̲model̲schema
の中で用いる。
6.4.1
solid̲model solid̲modelは,製品形状の完全な表現で,その内部にある点がすべて連結されてい
るものとする。あらゆる点は,立体の境界の内側,外側又は境界上のいずれかに分類できる。
立体モデルの表現には,幾つかの異なる形式かある。
EXPRESSによる定義
*)
ENTITY solid̲model
SUPERTYPE OF (ONEOF( csg̲solid,manifold̲solid̲brep, swept̲face̲solid,
swept̲area̲solid, solid̲replica))
SUBTYPE OF (geometric̲representation̲item);
END̲ENTITY;
(*
6.4.2
manifold̲solid̲brep manifold̲solid̲brepは,一つ以上の曲面によって境界付けられた有限で弧状
連結な空間領域とする。これらの曲面は,それぞれ,連結,かつ向き付けされ,有限で閉じた2-多様体と
する。貫通穴の個数及び空間領域における空洞(void)の個数に制限はない。
多様体立体の境界表現(B-rep)は,稜線及び頂点のグラフを利用する。このグラフは,連結,かつ向き
付けされ,有限で閉じた2-多様体の曲面に埋め込まれる。埋め込まれたグラフは,曲面を弧状連結である
領域(面)に分割する。したがって,稜線及び頂点は面の境界を形作り,面の定義域は境界を含まない。
埋め込まれたグラフは,非連結であること及び疑似グラフであることが許される。グラフは,名前付けさ
れる。すなわち,グラフの中の各要素は,一意に同定される。面の幾何を定める曲面は,面の定義域内で
平面に埋込み可能な2-多様体でなければならない。言い換えると,その曲面は,連結,かつ向き付けされ,
有限で自己干渉しておらず,曲面の種数が0でなければならない。
面は,境界以外では互いに交差しない。面の境界である各稜線は,たかだか1個の他の面に共有される。
境界表現の各稜線は,稜線の境界(すなわち,頂点)以外では交差しない。稜線の幾何を定める曲線は,
弧状連結でなければならず,稜線の定義域の中で自己干渉することも重なることも許されない。稜線の幾
何は,それを境界の一部とする
面の幾何に対して,整合しなければならない。
頂点の定義に用いる幾何は,それが境界の一部とする面及び稜線の幾何に対して,整合しなければなら
ない。
境界表現は,互いに分離している1個以上のclosed̲shellによって表現される。外殻の1個のシェルだけ
が,他のすべてのシェルを完全に包み,それ以外のシェルは,他のシェルを包まない。1個以上の空洞を
もつ境界表現の定義には,下位型brep̲with̲voidsが用意される。次のオイラー式が満足されなければなら
ない。
Xms=ν+ε+2F−Ll−2(S−gs)=0 ··················································· (10)
ここで,ν,ε,F,Ll及びSは,それぞれ,モデルにおける一意な頂点,稜線,面,面の境界及びシェルの
個数とし,gsはシェルの種数の総和とする。
144
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
具体的には,位相のエンティティは,次の制約に従わなければならない。ここで,Bは,多様体立体の
境界表現とする。
− 各シェルは,一意でなければならない。
(B)[S]=(B){S}
− 境界表現におけるそれぞれの面は,一意とする。
((B)[S])[F]=((B)[S]){F}
− それぞれのループは,一意とする。
(((B)[S])[F])[L]=(((B)[S])[F]){L}
− それぞれの(稜線+論理)の対は,一意とする。
((((B)[S])[F])[L])[El]=((((B)[S])[F])[L]){El}
− 境界表現におけるそれぞれの稜線は,ちょうど2個のループによって用いられるか,1個のルー
プに2回用いられるかのいずれかとする。
|((((B)[S])[F])[L]){El}|=2|((((B)[S])[F])[L])[El]|
すなわち,リスト((((B)[S])[F])[L])[E]において,それぞれの稜線は,ちょうど2回現れる。
− 式(10)を満足しなければならない。
2|(B)[S]|−2ΣGs=|(((((B)[S])[F]){Le}){E}){V}|+|((((B)[S])[F]){Lυ}){V}|
−|((((B)[S])[F]){L}){E}|+2|((B)[S])[F]|−|(((B)[S])[F])[L]|
境界表現の位相上の法線は,境界上の各点において,立体の内側から遠ざかる方向を指す曲面の法線の
方向とする。境界表現に用いられているclosed̲shellの法線は,境界表現の位相上の法線と整合しなければ
ならない。
manifold̲solid̲brepは,faceted̲brep及びbrep̲with̲voidsの2個の下位型をもち,それらには,暗黙のANDOR
関係が存在する。次は,すべてインスタンス化される。
− manifold̲solid̲brep
− brep̲with̲voids
− faceted̲brep
− faceted̲brep AND brep̲with̲voids
EXPRESSによる定義
*)
ENTITY manifold̲solid̲brep
SUBTYPE OF (solid̲model);
outer : closed̲shell;
END̲ENTITY;
(*
属性定義
outer:立体の外部の境界を定義するclosed̲shell。shellの法線は,立体の内部から遠ざかる方向を指さなけ
ればならない。
非形式的要件
IP1:manifold̲solid̲brepの次元数は,3とする。
IP2:manifold̲solid̲brepの大きさは,有限であって,かつ0でない。
IP3:manifold̲solid̲brepの参照するvertex̲point,向き付けされていない(すなわち,oriented̲edgeではな
145
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い)edge̲curve,又は向き付けされていない(すなわち,oriented̲faceではない)face̲surfaceは,同じ
manifold̲solid̲brepの参照する他のいかなる,vertex̲point,向き付けされていないedge̲curve,又は向き付
けされていないface̲surfaceと交差しない。
IP4:同一のfaceが参照する異なるloop同士は,共通のvertexをもたない。
備考 これは,同じ面にある別のloopが,共通のedgeをもたないことを意味する。幾何が存在する
場合,同じfaceの異なるloop同士は,交差しない。
IP5:manifold̲solid̲brepのすべての位相上の要素には,関連付けられた幾何が定義されている。
IP6:shellの法線は,境界表現の法線と一致し,かつ境界表現で表される立体から遠ざかる方向を指さな
ければならない。
IP7:それぞれのfaceは,manifold̲solid̲brepのshellから1回だけ参照されなければならない。
IP8:manifold̲solid̲brepにおけるそれぞれのoriented̲edgeは,1回だけ参照されなければならない。
IP9:それぞれの向き付けされていないedgeは,manifold̲solid̲brepのshellのfaceの中のloopから,ちょ
うど2回参照されなければならない。
IP10:境界表現に関するオイラー式は,満足されなければならない。このとき,種数の項gsは,境界表現
の各shellの種数の総和とする。
IP11:faceted̲brepでないmanifold̲solid̲brepは,poly̲loopを参照してはならない。
IP12:faceted̲brepは,faceの境界として,poly̲loopだけを参照できる。
6.4.3
brep̲with̲voids brep̲with̲voidsは,その内部に1個以上の空洞を含むmanifold̲solid̲brepの特別
な下位型とする。空洞は,oriented̲closed̲shellによって表現される。このとき,oriented̲closed̲shellの法
線は,空洞の内部を指す方向に定義される。すなわち,orientationは,FALSEとなる。brep̲with̲voidsは,
faceted̲brepとなることもできる。
EXPRESSによる定義
*)
ENTITY brep̲with̲voids
SUBTYPE OF (manifold̲solid̲brep);
voids : SET [1:?] OF oriented̲closed̲shell;
END̲ENTITY;
(*
属性定義
SELF\manifold̲solid̲brep.outer:立体の外部の境界を定義するoriented̲closed̲shell。shellの法線は,立体
の内部から遠ざかる方向を指さなければならない。
voids:立体の内部にある空洞を定義するoriented̲closed̲shellの集合。集合は,1個以上のshellを含んで
もよい。
非形式的要件
IP1:各空洞のshellは,外殻のshell及び他のすべての空洞のshellと分離していなければならない。
IP2:各空洞のshellは,外殻のshellの内部になければならず,他の空洞のshellの内部にあってはならな
い。ただし,外殻のshellは,空洞のshellの集合には含まれない。
IP3:manifold̲solid̲brepの各shellは,1回だけ参照される。
6.4.4
faceted̲brep faceted̲brepは,すべての面か平面であって,すべての稜線か直線である境界表現モ
デルの単純な形式とする。
146
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 曲面として平面だけもつ境界表現立体が大部分のシステムで認められていることから,そ
れらを支援するためにfaceted̲brepか導入された。多面体モデルは,manifold̲solid̲brepで
表現してもよいが,faceted̲brepとしての表現のほうがより簡潔である。
境界表現モデルと異なり,モデルの中で稜線及び頂点は,陽に表現されていないが,エンティティ
poly̲loopによって陰に参照可能とする。faceted̲brepは,manifold̲solid̲brepと同じ位相上の制約を満たさ
なければならない。
EXPRESSによる定義
*)
ENTITY faceted̲brep
SUBTYPE OF (manifold̲solid̲brep);
END̲ENTITY;
(*
非形式的要件
IP1:faceted̲brepに含まれるshellのfaceの境界をなすloopは,すべてpoly̲loop型とする。
IP2:shellに含まれるfaceは,曲面の幾何を陰にもっても陽にもってもよい。陽にもつ場合,face̲surface
は,平面とする。一つのfaceを定義しているpoly̲loopは,すべて共面とする。
6.4.5
csg̲solid CSGモデルとして表現される立体は,いわゆる基本立体(primitive solid)の集まりで定
義される。これらは,正規化されたブール操作によって結合される,積,和及び差の演算が許される。特
別な場合として,CSG立体を1個のCSG基本立体で構成することもできる。
正規化された空間の部分集合とは,点集合に基づく位相幾何学の通常の意味で,その集合の内部の閉包
をいう。boolean̲resultにとって,正規化は,もともとの演算によって生成される懸垂稜線及び他の不正規
な要素を除去する効果をもつ。
CSG立体を完全に定義するためには,幾何及び構造に関する2種類の情報を必要とする。
幾何に関する情報は,solid̲modelによって伝達される。これらは,典型的には,円柱,角柱,掃引のよ
うな基本立体であるが,一般の境界表現モデルを含むこともできる。solid̲modelは,solid̲replica(変換さ
れた立体)及びhalf̲space̲solidを含むこともできる。
構造に関する情報は,boolean̲resultとcsg̲primitiveとからなる木(非循環な有向グラフ)にある。これ
は,立体を構成するための“調理法”を表現している。末端の節点は,基本立体,その他の立体とする。
あらゆるcsg̲solidは,その立体を定義する木の根となるboolean̲resultをちょうど1個もつ(更に,木の
中に演算項として,boolean̲resultがあってもよい。)。エンティティcsg̲solidは,関係付けられた木で定義
される立体を,木の中のある特別なオブジェクトとして識別するために使われる。これによって,csg̲solid
は,構成過程での中間的な結果を表現する他のエンティティboolean̲resultと区別される。
EXPRESSによる定義
*)
ENTITY csg̲solid
SUBTYPE OF (solid̲model);
tree̲root̲expression : csg̲select;
END̲ENTITY;
(*
属性定義
147
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
tree̲root̲expression:基本立体及び正規化された演算子からなる,立体を記述するブール表現。ブール表現
の木の根は,エンティティboolean̲result又はエンティティcsg̲primitiveとして,陽に与えられる。
6.4.6
boolean̲result boolean̲resultは,2個の立体から1個の新しい立体を生成するための正規化され
た演算の結果とする。有効な演算は,正規化された,和,積及び差とする。ブール操作においては,立体
は,点の正規化集合であるとみなされる。
最終的なboolean̲resultは,演算及び2個の演算項に依存する。差の演算子の場合,演算項の順序も意味
をもつ。演算子は,union,intersection又はdifferenceのいずれでもよい。これらの演算子の効果は,次の
とおりとする。
2個の立体についてのunionは,first̲operand,second̲operandのいずれか,又は両方の内部のすべての
点からなる新しい立体とする。
2個の立体についてのintersectionは,first̲operandとsecond̲operandとの両方に含まれるすべての点の集
合を正規化した新しい立体とする。
2個の立体についてのdifferenceは,first̲operandの中に含まれるがsecond̲operandには含まれないすべ
ての点の集合を正規化した新しい立体とする。
備考 例えば,1番目の演算項が直方体で,2番目の演算項が適当な大きさ及び配置の円柱とする
と,演算子differenceで生成されたboolean̲resultは,円柱状の穴をもつ直方体となる。
EXPRESSによる定義
*)
ENTITY boolean̲result
SUBTYPE OF (geometric̲representation̲item);
operator
: boolean̲operator;
first̲operand
: boolean̲operand;
second̲operand
: boolean̲operand;
ENDENTITY;
(*
属性定義
operator:結果を作るための演算に用いられるboolean̲operator。
first̲operand:ブール操作が適用される1番目のboolean̲operand。
second̲operand:ブール操作が適用される2番目のboolean̲operand。
6.4.7
sphere sphere(球)は,中心及び半径によって定義される球の形をしたCSG基本立体とする。
EXPRESSによる定義
*)
ENTITY sphere
SUBTYPE OF (geometric̲representation̲item);
radius : positive̲length̲measure;
centre : point;
END̲ENTITY;
(*
属性定義
radius:sphereの半径。
148
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
centre:sphereの中心の配置。
6.4.8
right̲circular̲cone right̲circular̲cone(直円錐)は,先端の切落としが許される円錐の形をした
CSG基本立体とする。これは,軸,軸上の点,円錐の半頂角,半径及び距離によって定義される。円錐の
底面は,軸上の点から軸とは逆の方向に,この距離の位置に存在する。半径が0でなければ,円錐の切り
落とされた面の大きさ及び配置を与える。
EXPRESSによる定義
*)
ENTITY right̲circular̲cone
SUBTYPE OF (geometric̲representation̲item);
position : axis1̲placement;
height
: positive̲length̲measure;
radius
: length̲measure;
semi̲angle : plane̲angle̲measure;
WHERE
WR1: radius >= 0.0;
END̲ENTITY;
(*
属性定義
position:軸上の点の配置及び軸の方向。
position.location:円錐の軸上にある点で,円盤(平面で円状の面)の中心となるか,radiusが0に等しけれ
ば,頂点となる。
position.axis:円錐の中心軸(対称軸)の方向。
height:radiusが0より大きければ,円錐の二つの円盤の間の距離。radiusが0に等しければ,底面から頂
点までの距離。
radius:軸上の点(position.location)における円錐の半径。radiusが0に等しければ,その点が頂点となる。
radiusが0より大きければ,円錐は,先端が切り落とされている。
semi̲angle:円錐の頂角の半分。これは,軸と円錐面の母線との間の角度とする。
形式的要件
WR1:radiusは,負であってはならない。
非形式的要件
IP1:semi̲angleは,0°を超え90°未満でなければならない。
6.4.9
right̲circular̲cylinder right̲circular̲cylinder(直円柱)は,有限な高さの円柱の形をしたCSG基
本立体とする。これは,軸上の点で一方の円盤(平面で円状の面)の中心,高さ及び半径によって定義さ
れる。円盤は,軸に垂直で,指定された半径をもつ。高さは,軸の正の方向で,最初の円盤の中心から,2
番目の円盤の中心までの距離とする。
EXPRESSによる定義
*)
ENTITY right̲circular̲cylinder
SUBTYPE OF (geometric̲representation̲item);
position : axis1̲placement;
149
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
height
: positive̲length̲measure;
radius
: positive̲length̲measure;
END̲ENTITY;
(*
属性定義
position:軸上のpointの配置及び軸の方向。
position.location:円柱の軸の上にあって,円盤の上にあるpoint。
position.axis:円柱の中心の対称軸の方向。
height:円柱の二つの円盤の間の距離。
radius:円柱の半径。
6.4.10 torus torus(輪環体,トーラス)は,大きい方の円(準線)の回りに,もう一方の円(母線)の領
域を掃引することによって定義される基本立体とする。準線は,配置及び方向(axis̲placement)によって
定義される。
EXPRESSによる定義
*)
ENTITY torus
SUBTYPE OF (geometric̲representation̲item);
position : axis1̲placement;
major̲radius
: positive̲1ength̲measure;
minor̲radius
: positive̲length̲measure;
WHERE
WR1: major̲radius > minor̲radius;
END̲ENTITY;
(*
属性定義
position:軸上の中心のpointの配置及び軸の方向。これは,準線の中心及び平面を定義する。
major̲radius:準線の半径。
minor̲radius:母線の半径。
形式的要件
WR1:major̲radiusは,minor̲radiusより大きくなければならない。
6.4.11 block block(直方体)は,配置座標系によって定義される直交平行六面体とする。blockは,配置
座標系の軸に沿った正の長さx,y及びzによって指定され,配置座標系の原点に1個の頂点をもつ。
EXPRESSによる定義
*)
ENTITY block
SUBTYPE OF (geometric̲representation̲item);
position : axis2̲placement̲3d;
x
: positive̲length̲measure;
y
: positive̲length̲measure;
z
: positive̲length̲measure;
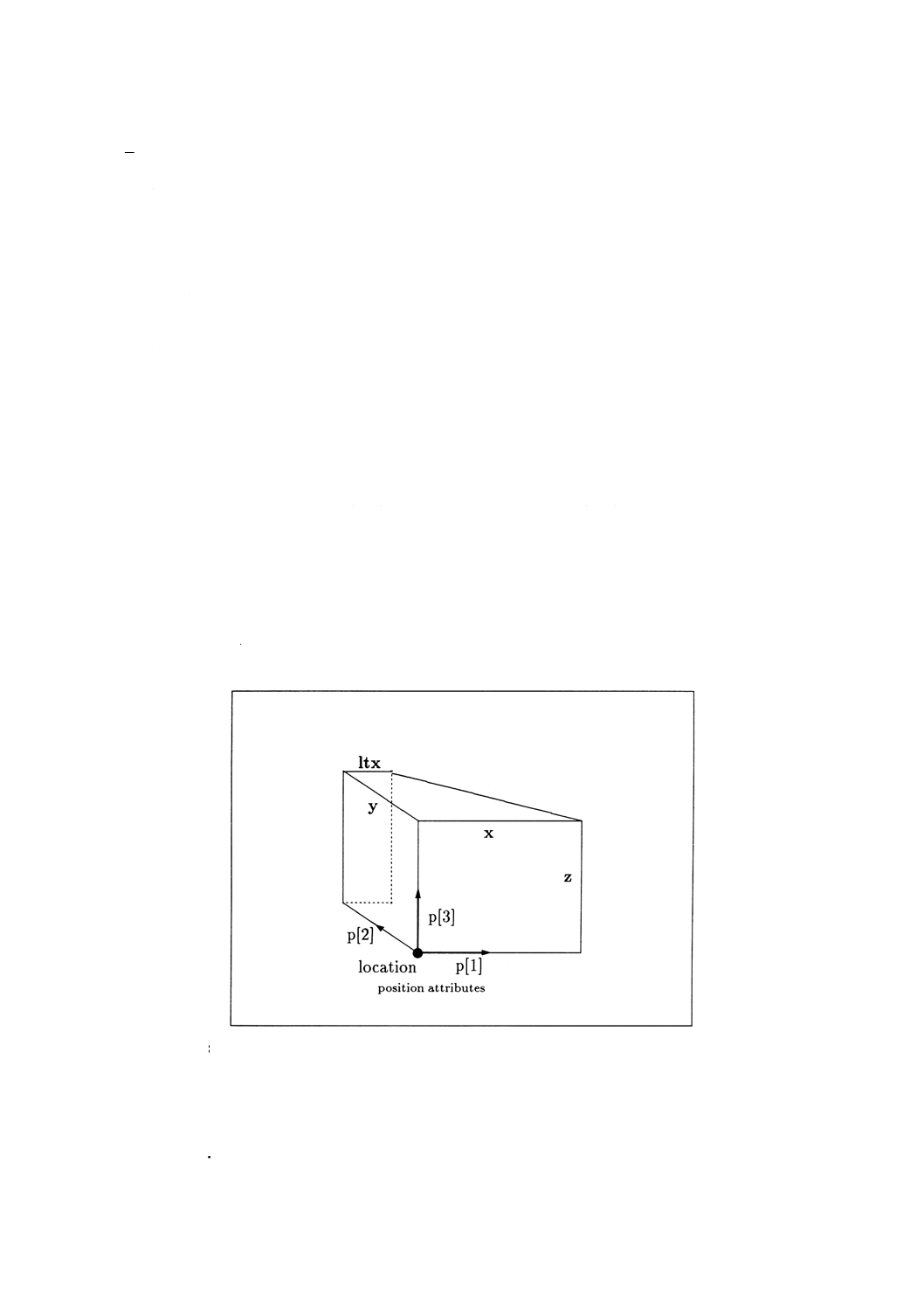
150
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲ENTITY;
(*
属性定義
position:blockを定義する座標系の配置及び向き。blockは,position.locationに1個の頂点をもち,その稜
線を配置座標系の軸の正の向きに並べる。
x:配置のX軸に沿ったblockの大きさ(position.p[1])。
y:配置のY軸に沿ったblockの大きさ(position.p[2])。
z:配置のZ軸に沿ったblockの大きさ(position.p[3])。
6.4.12 right̲angular̲wedge right̲angular̲wedgeは,直方体とその面のうちの一つに対して垂直な平面と
の交差の結果とする。それは,配置座標系によって定義される。三角形又は不等辺四角形の面は,配置の
X軸及びY軸によって定義される平面内に位置する。この面は,X軸及びY軸に沿った正の長さxの辺及
びyの辺,配置の原点から距離yでX軸に平行な長さltxの辺(ltxが0でない場合),並びにxの辺の終
点とltxの辺の終点とを結ぶ辺によって,指定される。right̲angular̲wedgeの残りの部分は,不等辺四角形
又は三角形が掃引される距離を定義する配置のZ軸に沿った正の長さzによって指定される。
right̲angular̲wedgeは,ltxが0の場合5個の面をもち,それ以外の場合6個の面をもつ。
備考 属性の解釈は,図12による。
EXPRESSによる定義
*)
ENTITY right̲angular̲wedge
SUBTYPE OF (geometric̲representation̲item);
図12 right̲angular̲wedge及び属性
position : axis2̲placement̲3d;
x
: positive̲length̲measure;
y
: positive̲length̲measure;
z : positive̲length̲measure;
ltx
: length̲measure;
151
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WHERE
WR1: ((0.0 <= ltx) AND (ltx < x));
END̲ENTITY;
(*
属性定義
position:right̲angular̲wedgeのための配置の座標系の配置及び向き。right̲angular̲wedgeは,position.location
に1個の頂点及び複数の稜線をもち,それらの稜線は,配置の軸の正の向きに配置される。
x:配置のX軸に沿ったright̲angular̲wedgeの大きさ。
y:配置のY軸に沿ったright̲angular̲wedgeの大きさ。
z:配置のZ軸に沿ったright̲angular̲wedgeの大きさ。
ltx:right̲angular̲wedgeのX方向(正の向き)の短い方の長さ。
形式的要件
WR1:ltxは,負であってはならず,かつxより小さくなければならない。
6.4.13 swept̲face̲solid swept̲face̲solidは,平面図形を掃引することによって手続き的に定義される。
swept̲face̲solidの空間における位置は,swept̲faceの位置に依存する。swept̲faceは,角度が360°の回転
による立体の場合を除いて,swept̲face̲solidの面になる。
EXPRESSによる定義
*)
ENTITY swept̲face̲solid
SUPERTYPE OF (ONEOF(extruded̲face̲solid, revolved̲face̲solid))
SUBTYPE OF (solid̲model);
swept̲face : face̲surface;
WHERE
WR1: 'GEO:METRY̲SCHEMA.PLANE' IN TYPEOF(swept̲face.face̲geometry);
END̲ENTITY;
(*
属性定義
swept̲face:掃引される領域を定義するface̲surface。この面の大きさは,参照されるface̲surfaceの属性
boundsによって定義される。
形式的要件
WR1:swept̲faceは,平面図形でなければならない。参照されるface̲surfaceの属性face̲geometryは,plane
とする。
6.4.14 extruded̲face̲solid extruded̲face̲solidは,平面のfaceを掃引することによって定義される立体と
する。平行移動の方向はベクトルdirectionによって定義され,平行移動の長さは距離depthによって定義
される。平面のfaceは穴をもつことができ,それは,掃引の結果,立体の穴となる。
EXPRESSによる定義
*)
ENTITY extruded̲face̲solid
SUBTYPE OF (swept̲face̲solid);
extruded̲direction : direction;
152
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
depth : positive̲length̲measure;
WHERE
WR1: dot̲product(
(SELF\swept̲face̲solid.swept̲face.face̲geometry\
elementary̲surface.position.p[3])
, extruded̲direction) <> 0.0;
END̲ENTITY;
(*
属性定義
SELF\swept̲face̲solid.swept̲face:掃引して立体を生成するface。
extruded̲direction:faceが掃引されるdirection。
depth:faceが掃引される距離。
形式的要件
WR1:extruded̲directionは,掃引されるfaceの平面の法線に垂直であってはならない。
6.4.15 revolved̲face̲solid revolved̲face̲solidは,ある軸回りに平面のfaceを回転することによって生成
される立体とする。軸は,faceと同一平面内になければならないが,faceの内部と交差してはならない。
平面のfaceは穴をもつことができ,それは掃引の結果,立体の穴となる。回転の方向は,軸の正方向に沿
って見たとき,時計回りとする。より正確には,Aを軸の配置,dを軸の方向,pをfaceの境界上の任意
の点とし,pによって生成される弧をCとすると,faceを回転する際,Cは,pにおいてd×(p−A)の方向
にある。
備考 属性の解釈は,図13による。
EXPRESSによる定義
*)
ENTITY revolved̲face̲solid
SUBTYPE OF (swept̲face̲solid);
axis : axis1̲placement;
angle : plane̲angle̲measure;
DERIVE
axis̲line : line := line(axis.location,vector(axis.z,1.0));
END̲ENTITY;
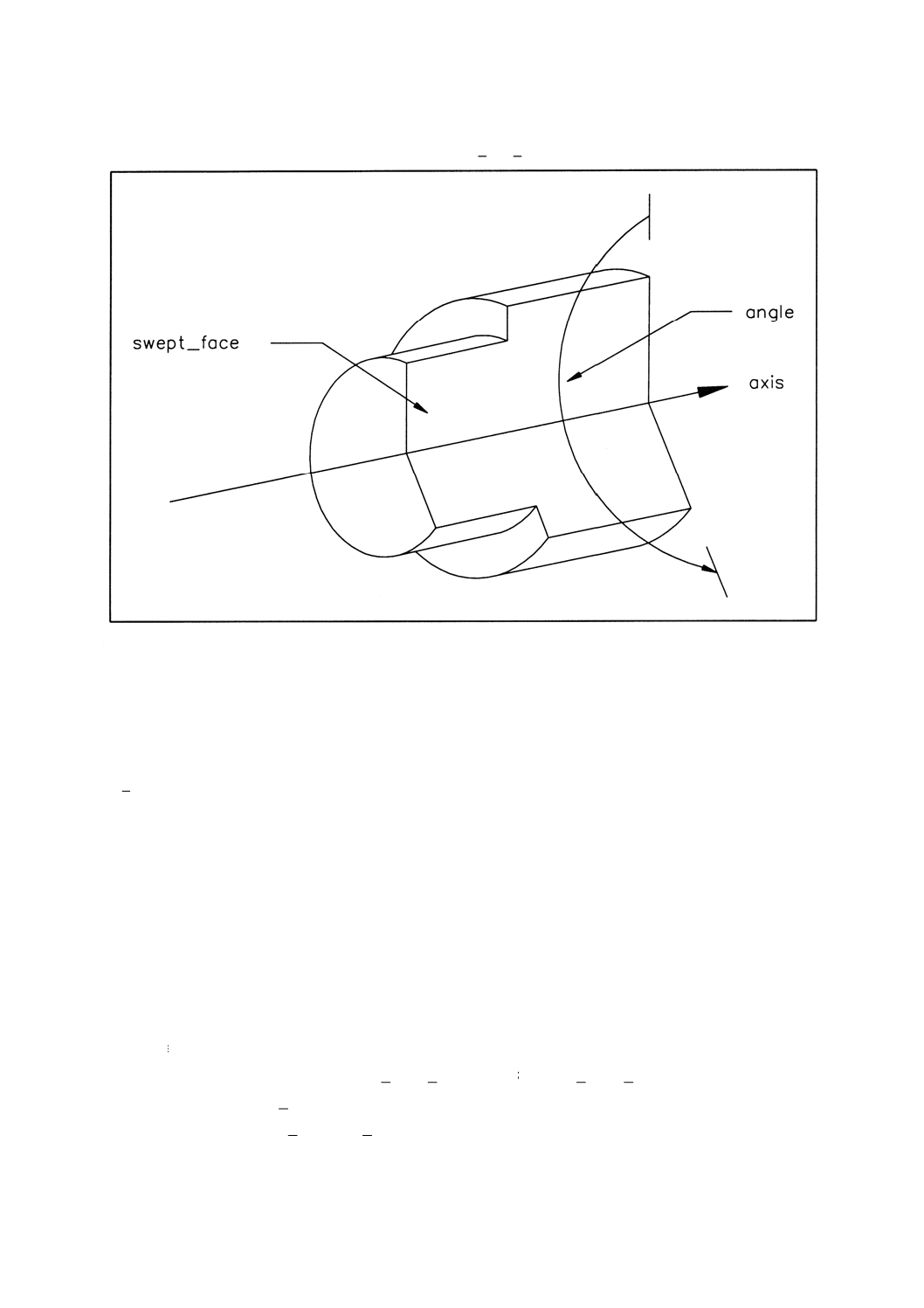
153
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図13 revolved̲face̲solid
(*
属性定義
SELF\swept̲face̲solid.swept̲face:回転して立体を生成するface。
axis:その回りで回転が起こる軸。
angle:回転の角度。この角度は,swept̲faceの平面から測られる。
axis̲line:回転の軸の直線。
非形式的要件
IP1:axis̲lineは,上位型swept̲face̲solidの属性swept̲faceの平面の上になければならない。
IP2:axis̲lineは,swept̲faceの内部と交差してはならない。
IP3:angleは,0〜360°の間とする。
6.4.16 swept̲area̲solid swept̲area̲solidは,境界付けられた平面の領域を掃引することによって手続き
的に定義されるエンティティとする。swept̲area̲solidの空間における位置は,swept̲areaの位置に依存す
る。swept̲areaは,角度が360°のrevolved̲area̲solidの場合を除いて,swept̲area̲solidの面になる。
EXPRESSによる定義
*)
ENTITY swept̲area̲solid
SUPERTYPE OF (ONEOF(revolved̲area̲solid, extruded̲area̲solid))
SUBTYPE OF (solid̲model);
swept̲area : curve̲bounded̲surface;
WHERE
154
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WR1: 'GEOMETRY̲SCHEMA.PLANE' IN TYPEOF(swept̲area.basis̲surface);
END̲ENTITY;
(*
属性定義
swept̲area:掃引される領域を定義するcurve̲bounded̲surface。この領域の大きさは,参照される
curve̲bounded̲surfaceの属性boundariesによって定義される。
形式的要件
WR1:swept̲areaは,平面でなければならない。参照されるcurve̲bounded̲surfaceの属性basis̲surfaceは,
planeとする。
6.4.17 extruded̲area̲solid extruded̲area̲solidは,境界付けられた平面の領域を掃引することによって定
義される立体とする。平行移動の方向は,ベクトルdirectionによって定義され,平行移動の長さは距離depth
によって定義される。平面の領域は穴をもつことかでき,それは,掃引の結果,立体の穴となる。
EXPRESSによる定義
*)
ENTITY extruded̲area̲solid
SUBTYPE OF (swept̲area̲solid);
extruded̲direction : direction;
depth
: positive̲length̲measure;
WHERE
WR1: dot̲product(
(SELF\swept̲area̲solid.swept̲area.basis̲surface\
elementary̲surface.position.p[3])
extruded̲direction) <> 0.0;
END̲ENTITY;
(*
属性定義
SELF\swept̲area̲solid.swept̲area:掃引して立体を生成する境界付けられた曲面の領域。
extruded̲direction:領域が掃引されるdirection。
depth:領域が掃引される距離。
形式的要件
WR1:extruded̲directionは,swept̲areaの平面の法線に垂直であってはならない。
6.4.18 revolved̲area̲solid revolved̲area̲solidは,境界付けられた平面の領域をある軸を中心に回転する
ことによって生成される立体とする。軸は,領域と同平面内になければならないが,その境界付けられた
平面の領域の内部と交差してはならない。境界付けられた平面の領域は,穴をもつことができ,掃引の結
果,立体の穴となる。回転の方向は,軸の正方向に沿って見たとき,時計回りとする。より正確には,A
を軸の配置,dを軸の方向,pを平面の領域の境界上の任意の点とし,pによって生成される回転の弧をC
とすると,領域を回転する際,Cは,pにおいてd×(p−A)の方向にある。
EXPRESSによる定義
*)
ENTITY revolved̲area̲solid
155
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SUBTYPE OF (swept̲area̲solid);
axis : axis1̲placement;
angle : plane̲angle̲measure;
DERIVE
axis̲line : line := line(axis.location,vector(axis.z,1.0));
END̲ENTITY;
(*
属性定義
SELF\swept̲area̲solid.swept̲area:回転して立体を生成するcurve̲bounded̲surface。
axis:その回りで回転が起こる軸。
angle:掃引の角度。この角度は,swept̲areaの平面から測られる。
axis̲line:回転の軸の直線。
非形式的要件
IP1:axis̲lineは,上位型swept̲area̲solidの属性swept̲areaの平面上になければならない。
IP2:axis̲lineは,swept̲areaの内部と交差してはならない。
IP3:angleは,0〜360°の間とする。
6.4.19 half̲space̲solid half̲space̲solidは,半空間によって定義される。半空間は,境界のない曲面の片
側にあり,定義空間の正規部分集合とする。定義空間は,下位型boxed̲half̲spaceの直方体によって制限
される。曲面のどちら側が半空間に含まれるかは,曲面の法線及びagreement̲flagによって決められる。
agreement̲flagがTRUE(真)ならば,部分集合は,法線がその内側から遠ざかる側にある。agreement̲flag
がFALSE(偽)ならば,部分集合は,法線と同じ側にある。
有効なhalf̲space̲solidについて,曲面は,ちょうど2個の部分集合に定義空間を分割しなければならな
い。更に,定義空間の中で,曲面は多様体とし,かつ曲面のすべての法線は同一の部分集合の側を指す。
備考 half̲space̲solidは,solid̲modelの下位型ではない。half̲space̲solidは,ブール式の演算項
としてだけ有効とする。
EXPRESSによる定義
*)
ENTITY half̲space̲solid
SUBTYPE OF(geometric̲representation̲item);
base̲surface
: surface;
agreement̲flag
: BOOLEAN;
END̲ENTITY;
(*
属性定義
base̲surface:半空間の境界を定義するsurface。
agreement̲flag:base̲surfaceの法線がhalf̲space̲solidの実体から遠ざかる方を指す場合,agreement̲flagは,
TRUEとする。
非形式的要件
IP1:base̲surfaceは,定義空間をちょうど二つの部分集合に分けなければならない。half̲space̲solidが下
位型のboxed̲half̲spaceである場合,その定義域は,属性enclosureの定義域とする。それ以外の場合,定
156
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
義域は全空間となり,base̲surfaceは境界をもってはならない。
参考 “定義空間”は,原国際規格では“domain”とされている。half̲space̲solid自身の定義域
との違いを明確にするために,定義空間とした。
6.4.20 boxed̲half̲space boxed̲half̲spaceは,直方体によってトリムされるhalf̲space̲solidの下位型と
する。直方体は,幾何座標系の座標軸に平行な稜線をもつ。
備考 この直方体は,有限な大きさの立体を生成して,CSGの計算を容易にすることを目的とす
る。
EXPRESSによる定義
*)
ENTITY boxed̲half̲space
SUBTYPE OF(half̲space̲solid);
enclosure : box̲domain;
END̲ENTITY;
(*
属性定義
enclosure:計算上の目的で,半空間を境界付ける直方体。
6.4.21 box̲domain box̲domainは,幾何座標系の軸に平行に向き付けられた直方体とし,half̲space̲solid
の定義空間を制限する場合に使う。box̲domainは,すべての座標値が最小となる頂点及び座標軸の方向に
測られる辺の長さで指定される。
EXPRESSによる定義
*)
ENTITY box̲domain;
corner
: cartesian̲point;
xlength : positive̲length̲measure;
ylength : positive̲1ength̲measure;
zlength : positive̲length̲measure;
WHERE
WR1: SIZEOF(QUERY(item <* USEDIN(SELF,'')|
NOT ('GEOMETRIC̲MODEL̲SCHEMA.BOXED̲HALF̲SPACE'
IN TYPEOF(item)))) = 0;
END̲ENTITY;
(*
属性定義
corner:直方体の頂点のうち,すべての座標値が最小となるもの。
xlength:x軸に平行な稜線に沿ったbox̲domainの長さ。
ylength:y軸に平行な稜線に沿ったbox̲domainの長さ。
zlength:z軸に平行な稜線に沿ったbox̲domainの長さ。
形式的要件
WR1:box̲domainは,boxed̲half̲spaceを定義する場合に限り用いる。
6.4.22 solid̲replica solid̲replicaは,新しい配置における立体の複製とする。
157
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
ENTITY solid̲replica
SUBTYPE OF (solid̲model);
parent̲solid
: solid̲model;
transformation
: cartesian̲transformation̲operator̲3d;
WHERE
WR1: acyclic̲solid̲replica(SELF, parent̲solid);
END̲ENTITY;
(*
属性定義
parent̲solid:solid̲replicaを作るために複製される立体モデル。
transformation:solid̲replicaの配置及び向きを定義するcartesian̲transformation̲operator̲3d。拡大・縮小が
適用される場合,その係数も定義する。
形式的要件
WR1:solid̲replicaは,それ自身の定義に関係してはならない。
6.4.23 shell̲based̲surface̲model shell̲based̲surface̲modelは,次元数2のopen̲shell又はclosed̲shell
の集合によって記述される。シェル同士は,頂点,稜線,及び面を共有する場合を除き,互いに交差して
はならない。シェルの共有部分は,同一の面,稜線及び頂点を参照しなければならない。
少なくとも1個のshellがなければならない。
shellは,surface̲modelとは独立に存在してもよい。
EXPRESSによる定義
*)
ENTITY shell̲based̲surface̲model
SUBTYPE OF (geometric̲representation̲item);
sbsm̲boundary : SET [1:?] OF shell;
WHERE
WR1: constraints̲geometry̲shell̲based̲surface̲model(SELF);
END̲ENTITY;
(*
属性定義
sbsm̲boundary:surface̲modelを定義するshellの集合。
形式的要件
WR1:shell̲based̲surface̲modelを構成するshellの型は,open̲shell又はclosed̲shellに限られる。
非形式的要件
IP1:shell̲based̲surface̲modelの次元数は,2とする。
IP2:shellは,共通のface,edge又はvertexを除いて,重なったり交差したりしてはならない。
6.4.24 face̲based̲surface̲model face̲based̲surface̲modelは,次元数2のconnected̲face̲setの集合によ
って記述される。
connected̲face̲set同士は,頂点,稜線及び面を共有する場合を除き,互いに交差してはならない。
158
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
少なくとも1個のconnected̲face̲setがなければならない。
connected̲face̲setは,surface̲modelとは独立に存在してもよい。
EXPRESSによる定義
*)
ENTITY face̲based̲surface̲model
SUBTYPE OF (geometric̲representation̲item);
fbsm̲faces : SET [1:?] OF connected̲face̲set;
END̲ENTITY;
(*
属性定義
fbsm̲faces:face̲based̲surface̲modelを構成するconnected̲face̲setの集合。
非形式的要件
IP1:connected̲face̲setは,共通のface,edge又はvertexを除いて,重なったり交差したりしてはならな
い。
IP2:fbsm̲facesの次元数は,2とする。
6.4.25 shell̲based̲wireframe̲model shell̲based̲wireframe̲modelは,R3に埋め込まれた稜線及び頂点の
グラフによって記述される。グラフは,連結でなくてもよい。グラフの中で,稜線は,その境界(すなわ
ち,頂点)を除き,交差しない。
頂点に関連付けられる幾何は,その頂点を境界にもつ稜線に対し,稜線に関連付けられる幾何と整合し
なければならない。
shell̲based̲wireframe̲modelは,次元数か0又は1の1個以上のshellによって,表現される。
少なくとも1個のshellがなければならない。
shellは,wireframe̲modelとは独立に存在してもよい。
EXPRESSによる定義
*)
ENTITY shell̲based̲wireframe̲model
SUBTYPE OF (geometric̲representation̲item);
sbwm̲boundary : SET [1:?] OF shell;
WHERE
WR1: constraints̲geometry̲shell̲based̲wireframe̲model(SELF);
END̲ENTITY;
(*
属性定義
sbwm̲boundary:wireframe̲modelを構成するvertex̲shell及び/又はwire̲shellの集合。
形式的要件
WR1:それぞれのshellの型は,vertex̲shell又はwire̲shellでなければならない。関数
constraints̲geometry̲shell̲based̲wireframe̲modelは,これらの幾何制約を評価し,制約が満たされる場合
にTRUEを返す。
非形式的要件
IP1:sbwm̲boundaryの次元数は,1以下とする。
159
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IP2:shell̲based̲wireframe̲modelは,正で有限な大きさをもつ。
IP3:shellは,共通のedge又はvertexを除き,重なったり交差したりしてはならない。
6.4.26 edge̲based̲wireframe̲model edge̲based̲wireframe̲modelは,R3に埋め込まれた稜線及び頂点の
グラフによって記述される。グラフは,連結でなくてもよい。グラフの中で,稜線はその境界(すなわち,
頂点)を除き,交差しない。
頂点に関連付けられる幾何は,その頂点を境界にもつ稜線に対し,稜線に関連付けられる幾何と整合し
なければならない。
edge̲based̲wireframe̲modelは,次元数が1の1個以上のconnected̲edge̲setによって表現される。
少なくとも1個のconnected̲edge̲setがなければならない。
connected̲edge̲setは,wireframe̲modelとは独立に存在してもよい。
EXPRESSによる定義
*)
ENTITY edge̲based̲wireframe̲model
SUBTYPE OF (geometric̲representation̲item);
ebwm̲boundary : SET [1:?] OF connected̲edge̲set,
END̲FNTITY;
(*
属性定義
ebwm̲boundary:edge̲based̲wireframe̲modelを構成するconnected̲edge̲setの集合。
非形式的要件
IP1:edge̲based̲wireframe̲modelの次元数は,1とする。
IP2:connected̲edge̲setは,共通のedge又はvertexを除き,重なったり交差したりしてはならない。
6.4.27 geometric̲set geometric̲setは,位相構造が利用できないときに,モデルの交換のために用いる。
EXPRESSによる定義
*)
ENTITY geometric̲set
SUPERTYPE OF (ONEOF(geometric̲curve̲set,
geometric̲set̲replica))
SUBTYPE OF (geometric̲representation̲item);
elements : SET [1:?] OF geometric̲set̲select;
END̲ENTITY;
(*
属性定義
elements:geometric̲setを構成する幾何の要素であって,point,curve又はsurfaceとする。ただし,座標空
間の次元数は,同じでなければならない。
6.4.28 geometric̲curve̲set geometric̲curve̲setは,2次元又は3次元のpoint及びcurveの集まりとする。
EXPRESSによる定義
*)
ENTITY geometric̲curve̲set
SUBTYPE OF (geometric̲set);
160
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
WHERE
WR1: SIZEOF(QUERY(temp <* SELF\geometric̲set.elements |
'GEOMETRY̲SCHEMA.SURFACE' IN TYPEOF(temp))) = 0;
END̲ENTITY;
(*
属性定義
SELF\geometric̲set.elements:このgeometric̲setに含まれる要素。
形式的要件
WR1:このgeometric̲setには,曲面が含まれてはならない。
6.4.29 geometric̲set̲replica geometric̲set̲replicaは,異なる配置のgeometric̲setの複製を定義する。
geometric̲setの各要素は,同一のtransformation(拡大・縮小を含んでもよい。)によって変換される。生成
されたgeometric̲setの型は,parent̲setの型に一致する。
EXPRESSによる定義
*)
ENTITY geometric̲set̲replica
SUBTYPE OF (geometric̲set);
parent̲set : geometric̲set;
transformation
: cartesian̲transformation̲operator;
DERIVE
SELF\geometric̲set.elements : SET [1:?] OF geometric.set̲select :=
build̲transformed̲set(transformation, parent̲set);
WHERE
WR1: acyclic̲set̲replica(SELF, parent̲set);
END̲ENTITY;
(*
属性定義
parent̲set:geometric̲set̲replicaを作るために複製されるgeometric̲set。
transformation:geometric̲set̲replicaの配置及び向きを定義するcartesian̲transformation̲operator。
SELF\geometric̲set.elements:parent̲setにtransformationを適用した結果の要素の集合。
形式的要件
WR1:geometric̲set̲replicaは,それ自身の定義に関係してはならない。
6.5
geometric̲model̲schemaの関数定義
6.5.1
acyclic̲solid̲replica ブール関数acyclic̲solid̲replicaは,再帰的な関数であって,与えられた
solid̲replicaがそれ自身の定義の中に現れるかどうかを判定する。この関数は,solid̲replicaが,その定義
中で直接的又は間接的に,自らを参照する場合,FALSEを返す。
EXPRESSによる定義
*)
FUNCTION acyclic̲solid̲replica(rep : solid̲replica ; parent : solid̲model)
: BOOLEAN;
IF NOT (('GEOMETRY̲SCHEMA.SOLID̲REPLICA') IN TYPEOF(parent)) THEN
161
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
RETURN(TRUE);
END̲IF;
(* parent が solid̲replica 型でなければ TRUE を返す。*)
IF (parent :=: rep) THEN
RETURN(FALSE);
(* parent が同じ solid̲replica ならば FALSE を返す。
それ以外の場合は,parent 自身の parent̲solid で再び関数を呼ぶ。*)
ELSE RETURN(acyclic̲solid̲replica(rep,parent\solid̲replica.parent̲solid));
END̲IF;
END̲FUNCTION;
(*
引数定義
rep:(入力)循環的参照を検査するsolid̲replica。
parent:(入力)複製の定義に用いられるsolid̲model。
:(出力)repがそれ自身の定義で使われているとき,FALSEとなるブール変数。
6.5.2
acyclic̲set̲replica ブール関数acyclic̲set̲replicaは,再帰的な関数であって,与えられた
geometric̲set̲replicaがそれ自身の定義の中に現れるかどうかを判定する。この関数は,geometric̲set̲replica
が,その定義中で直接的又は間接的に,自らを参照する場合,FALSEを返す。
EXPRESSによる定義
*)
FUNCTION acyclic̲set̲replica(rep : geometric̲set̲replica;
parent : geometric̲set) : BOOLEAN;
IF NOT(('GEOMETRY̲SCHEMAGEOMETRIC̲SET̲REPLICA') IN TYPEOF(parent)) THEN
RETURN(TRUE);
END̲IF;
(* parent が geometric̲set̲replica 型でなければ,TRUE を返す。*)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* parent が同じ geometric̲set̲replica ならば FALSE を返す。
それ以外の場合は,parent 自身の parent̲set で同じ関数を呼ぶ。*)
ELSE RETURN(acyclic̲set̲replica(rep,
parent\geometric̲set̲replica.parent̲set));
END̲IF;
END̲FUNCTION;
(*
引数定義
rep:(入力)循環的参照を検査するgeometric̲set̲replica。
parent:(入力)複製の定義に用いられるgeometric̲set。
:(出力)repがそれ自身の定義で使われているとき,FALSEとなるブール変数。
162
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.5.3
constraints̲geometry̲shell̲based̲surface̲model この関数は,shell̲based̲surface̲modelに関する
幾何制約を評価し,制約か満たされる場合に,TRUEを返す。
EXPRESSによる定義
*)
FUNCTION constraints̲geometry̲shell̲based̲surface̲model
(m: shell̲based̲surface̲model): BOOLEAN;
LOCAL
result: BOOLEAN := TRUE;
END̲LOCAL;
REPEAT j := 1 TO SIZEOF(m.sbsm̲boundary);
IF (NOT('TOPOLOGY̲SCHEMA.OPEN̲SHELL' IN TYPEOF(m.sbsm̲boundary[j])) AND
(NOT('TOPOLOGY̲SCHEMA.CLOSED̲SHELL'IN TYPEOF(m.sbsm̲boundary[j]))))
THEN
result := FALSE;
RETURN(result);
(* surface̲model は,open̲shell と closed̲shell とからなる。*)
END̲IF;
END̲REPEAT;
RETURN(result);
END̲FUNCTION;
(*
引数定義
m:(入力)幾何制約を検証するshell̲based̲surface̲model。
result:(出力)mの境界かopen̲shell及びclosed̲shellだけからなるとき,TRUEとなるブール変数。
6.5.4
constraints̲geometry̲shell̲based̲wireframe̲model この関数は,shell̲based̲wireframe̲modelに
関する幾何制約を評価し,制約が満たされる場合にTRUEを返す。
EXPRESSによる定義
*)
FUNCTION constraints̲geometry̲shell̲based̲wireframe̲model
(m : shell̲based̲wireframe̲model) : BOOLEAN;
LOCAL
result: BOOLEAN := TRUE;
END̲LOCAL;
REPEAT j := 1 TO SIZEOF(m.sbwm̲boundary);
IF (NOT('TOPOLOGY̲SCHEMA.WIRE̲SHELL' IN TYPEOF(m.sbwm̲boundary[j])) AND
(NOT('TOPOLOGY̲SCHEMA.VERTEX̲SHELL' IN TYPEOF(m.sbwm̲boundary[j]))))
THEN
result := FALSE;
RETURN(result);
(* wireframe̲model は,wire̲shell と vertex̲shell とからなる。*)
163
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
END̲IF;
END̲REPEAT;
RETURN(result);
END̲FUNCTION;
(*
引数定義
m:(入力)幾何制約を検証するshell̲based̲wireframe̲model。
result:(出力)mの境界がwire̲shell及びvertex̲shellだけからなるとき,TRUEとなるブール変数。
6.5.5
build̲transformed̲set この関数は,入力されたgeometric̲setの個々の要素(曲線,点又は曲面)
に対し,cartesian̲transformation̲operatorで表される変換を適用して,新たな集合を生成する。
EXPRIESSによる定義
*)
FUNCTION build̲transformed̲set(tr : cartesian̲transformation̲operator;
gset : geometric̲set) : SET [0:?] OF geometric̲set̲select;
LOCAL
s : SET [1:?] OF geometric̲set̲select := gset.elements;
trset : SET [0:?] OF geometric̲set̲select := [];
trcurve : curve;
trpoint : point;
trsurf : surface;
END̲LOCAL;
REPEAT j := 1 TO SIZEOF(s);
IF ('GEOMETRY̲SCHEMA.CURVE' IN TYPEOF(s[j])) THEN
trset := trset + curve̲replica(s[j],tr); ELSE
IF ('GEOMETRY̲SCHEMA.POINT' IN TYPEOF(s[j])) THEN
trset := trset + point̲replica(s[j],tr); ELSE
IF ('GEOMETRY̲SCHEMA.SURFACE' IN TYPEOF(s[j])) THEN
trset := trset + surface̲replica(s[j],
tr || cartesian̲transformation̲operator̲3d (?));
END̲IF;
END̲IF;
END̲IF;
END̲REPEAT;
RETURN(trset);
END̲FUNCTION;
(*
引数定義
tr:(入力)変換を定義するcartesian̲transformation̲operator。
gse:(入力)変換されるgeometric̲set。
trset:(出力)変換された結果の集合。
164
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
EXPRESSによる定義
*)
END̲SCHEMA; -- geometric̲model̲schema の終了
(*

165
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) エンティティの短縮名
表A.1は,この規格で規定するエンティティの短縮名を示す。短縮名の使用に関する要件は,この規格
に関連する規格群で規定される実装方法の中で示す。
附属書A表A.1 エンティティの短縮名
エンティティ名
短縮名
AXIS1̲PLACEMENT
AX1PLC
AXIS2̲PLACEMENT̲2D
A2PL2D
AXIS2̲PLACEMENT̲3D
A2PL3D
BEZIER̲CURVE
BZRCRV
BEZIER̲SURFACE
BZRSRF
BLOCK
BLOCK
BOOLEAN̲RESULT
BLNRSL
BOUNDARY̲CURVE
BNDCR
BOUNDED̲CURVE
BNDCRV
BOUNDED̲PCURVE
BNDPCR
BOUNDED̲SURFACE
BNDSRF
BOUNDED̲SURFACE̲CURVE
BNSRCR
BOXED̲HALF̲SPACE
BXHLSP
BOX̲DOMAIN
BXDMN
BREP̲WITH̲VOIDS
BRWTVD
B̲SPLINE̲CURVE
BSPCR
B̲SPLINE̲CURVE̲WITH̲KNOTS
BSCWK
B̲SPLINE̲SURFACE
BSPSR
B̲SPLINE̲SURFACE̲WITH̲KNOTS
BSSWK
CARTESIAN̲POINT
CRTPNT
CARTESIAN̲TRANSFORMATION̲OPERATOR
CRTROP
CARTESIAN̲TRANSFORMATION̲OPERATOR̲2D
CTO2
CARTESIAN̲TRANSFORMATION̲OPERATOR̲3D
CTO3
CIRCLE
CIRCLE
CLOSED̲SHELL
CLSSHL
COMPOSITE̲CURVE
CMPCRV
COMPOSITE̲CURVE̲ON̲SURFACE
CCOS
COMPOSITE̲CURVE̲SEGMENT
CMCRSG
CONIC
CONIC
CONICAL̲SURFACE
CNCSRF
CONNECTED̲EDGE̲SET
CNEDST
CONNECTED̲FACE̲SET
CNFCST
CSG̲SOLID
CSGSLD
CURVE
CURVE
CURVE̲BOUNDED̲SURFACE
CRBNSR
CURVE̲REPLICA
CRVRPL
CYLINDRICAL̲SURFACE
CYLSRF
DEGENERATE̲PCURVE
DGNPCR
DEGENERATE̲TOROIDAL̲SURFACE
DGTRSR
DIRECT1ON
DRCTN
EDGE
EDGE

166
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
エンティティ名
短縮名
EDGE̲BASED̲WIREFRAME̲MODEL
EBWM
EDGE̲CURVE
EDGCRV
EDGE̲LOOP
EDGLP
ELEMENTARY̲SURFACE
ELMSRF
ELLIPSE
ELLPS
EVALUATED̲DEGENERATE̲PCURVE
EVDGPC
EXTRUDED̲AREA̲SOLID
EXARSL
EXTRUDED̲FACE̲SOLID
EXFCSL
FACE
FACE
FACETED̲BREP
FCTBR
FACE̲BASED̲SURFACE̲MODEL
FBSM
FACE̲BOUND
FCBND
FACE̲OUTER̲BOUND
FCOTBN
FACE̲SURFACE
FCSRF
GEOMETRIC̲CURVE̲SET
GMCRST
GEOMETRIC̲REPRESENTATION̲CONTEXT
GMRPCN
GEOMETRIC̲REPRESENTATION̲ITEM
GMRPIT
GEOMETRIC̲SET
GMTST
GEOMETRIC̲SET̲REPLICA
GMSTRP
HALF̲SPACE̲SOLID
HLSPSL
HYPERBOLA
HYPRBL
INTERSECTION̲CURVE
INTCRV
LINE
LINE
LOOP
LOOP
MANIFOLD̲SOLID̲BREP
MNSLBR
OFFSET̲CURVE̲2D
OFCR2D
OFFSET̲CURVE̲3D
OFCR3D
OFFSET̲SURFACE
OFFSRF
OPEN̲PATH
OPNPTH
OPEN̲SHELL
OPNSHL
ORIENTED̲CLOSED̲SHELL
ORCLSH
ORIENTED̲EDGE
ORNEDG
ORIENTED̲FACE
ORNFC
ORIENTED̲OPEN̲SHELL
OROPSH
ORIENTED̲PATH
ORNPTH
OUTER̲BOUNDARY̲CURVE
OTBNCR
PARABOLA
PRBL
PATH
PATH
PCURVE
PCURVE
PLACEMENT
PLCMNT
PLANE
PLANE
POINT
POINT
POINT̲ON̲CURVE
PNONCR
POINT̲ON̲SURFACE
PNONSR
POINT̲REPLICA
PNTRPL
POLYLINE
PLYLN
POLY̲LOOP
PLYLP
QUASI̲UNIFORM̲CURVE
QSUNCR
QUASI̲UNIFORM̲SURFACE
QSUNSR

167
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
エンティティ名
短縮名
RATIONAL̲B̲SPLINE̲CURVE
RBSC
RATIONAL̲B̲SPLINE̲SURFACE
RBSS
RECTANGULAR̲COMPOSITE̲SURFACE
RCCMSR
RECTANGULAR̲TRIMMED̲SURFACE
RCTRSR
REPARAMETRISED̲COMPOSITE̲CURVE̲SEGMENT
RCCS
REVOLVED̲AREA̲SOLID
RVARSL
REVOLVED̲FACE̲SOLID
RVFCSL
RIGHT̲ANGULAR̲WEDGE
RGANWD
RIGHT̲CIRCULAR̲CONE
RGCRCN
RIGHT̲CIRCULAR̲CYLINDER
RGCRCY
SEAM̲CURVE
SMCRV
SHELL̲BASED̲SURFACE̲MODEL
SBSM
SHELL̲BASED̲WIREFRAME̲MODEL
SBWM
SOLID̲MODEL
SLDMDL
SOLID̲REPLICA
SLDRPL
SPHERE
SPHERE
SPHERICAL̲SURFACE
SPHSRF
SUBFACE
SBFC
SURFACE
SRFC
SURFACE̲CURVE
SRFCRV
SURFACE̲OF̲LINEAR̲EXTRUSION
SL
SURFACE̲OF̲REVOLUTION
SROFRV
SURFACE̲PATCH
SRFPTC
SURFACE̲REPLICA
SRFRPL
SWEPT̲AREA̲SOLID
SWARSL
SWEPT̲FACE̲SOLID
SWFCSL
SWEPT̲SURFACE
SWPSRF
TOPOLOGICAL̲REPRESENTATION̲ITEM
TPRPIT
TOROIDAL̲SURFACE
TRDSRF
TORUS
TORUS
TRIMMED̲CURVE
TRMCRV
UNIFORM̲CURVE
UNFCRV
UNIFORM̲SURFACE
UNFSRF
VECTOR
VECTOR
VERTEX
VERTEX
VERTEX̲LOOP
VRTLP
VERTEX̲POINT
VRTPNT
VERTEX̲SHELL
VRTSHL
WIRE̲SHELL
WRSHL
168
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定) 情報オブジェクトの登録
開放型システムで情報オブジェクトをあいまいさなく識別するために,次のオブジェクト識別子をこの
規格自身に割り当てる。この値の意味は,ISO/IEC 8824-1で定義され,JIS B 3700-1で規定されている。
{iso standard 10303 part(42)version(1)}
開放型システムでgeometry̲schema(4.参照)をあいまいさなく識別するために,geometry̲schemaに対
して,次のオブジェクト識別子が割り当てられている。
{iso standard 10303 part(42)version(1)object(1)geometry-schema(1)}
この値の意味は,ISO/IEC 8824-1で定義され,JIS B 3700-1で規定されている。
開放型システムでtopology̲schema(5.参照)をあいまいさなく識別するために,topology̲schemaに対し
て,次のオブジェクト識別子が割り当てられている。
{iso standard 10303 part(42)version(1)object(1)topology-schema(2)}
この値の意味は,ISO/IEC 8824-1で定義され,JIS B 3700-1で規定されている。
開放型システムでgeometric̲model̲schema(6.参照)をあいまいさなく識別するために,
geometric̲model̲schemaに対して,次のオブジェクト識別子が割り当てられている。
{iso standard 10303 part(42)version(1)object(1)geometric-model-schema(3)}
この値の意味は,ISO/IEC 8824-1で定義され,JIS B 3700-1で規定されている。
169
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 計算機可読な一覧
この附属書は,エンティティの名称に対応する短縮名の一覧,及びこの規格におけるEXPRESSによる
定義の一覧を提供する。文又は注釈は,含まない。この附属書は,計算機可読な形式だけで提供される。
170
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考) EXPRESS-Gによる図式表現
この附属書の図D.1〜D.18は,附属書C(参考)に示すEXPRESSに対応する。これらの図は,EXPRESS
言語のための図式表現EXPRESS-Gを用いている。EXPRESS-Gは,JIS B 3700-11の附属書D(規定)に
規定されている。
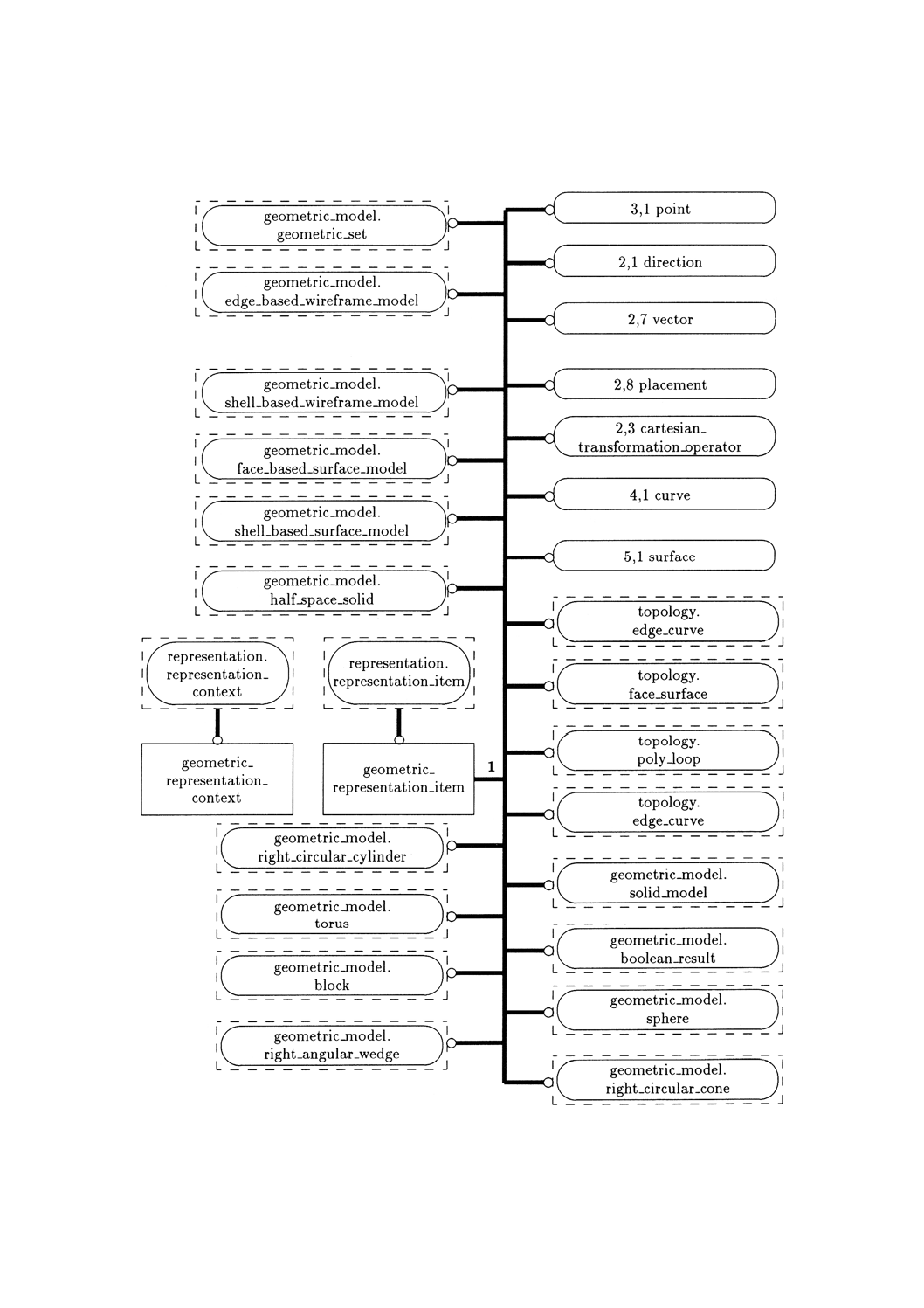
171
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.1 geometry̲schemaのEXPRESS-Gによる図式表現(1/12)
−geometric̲representation̲itemの下位型
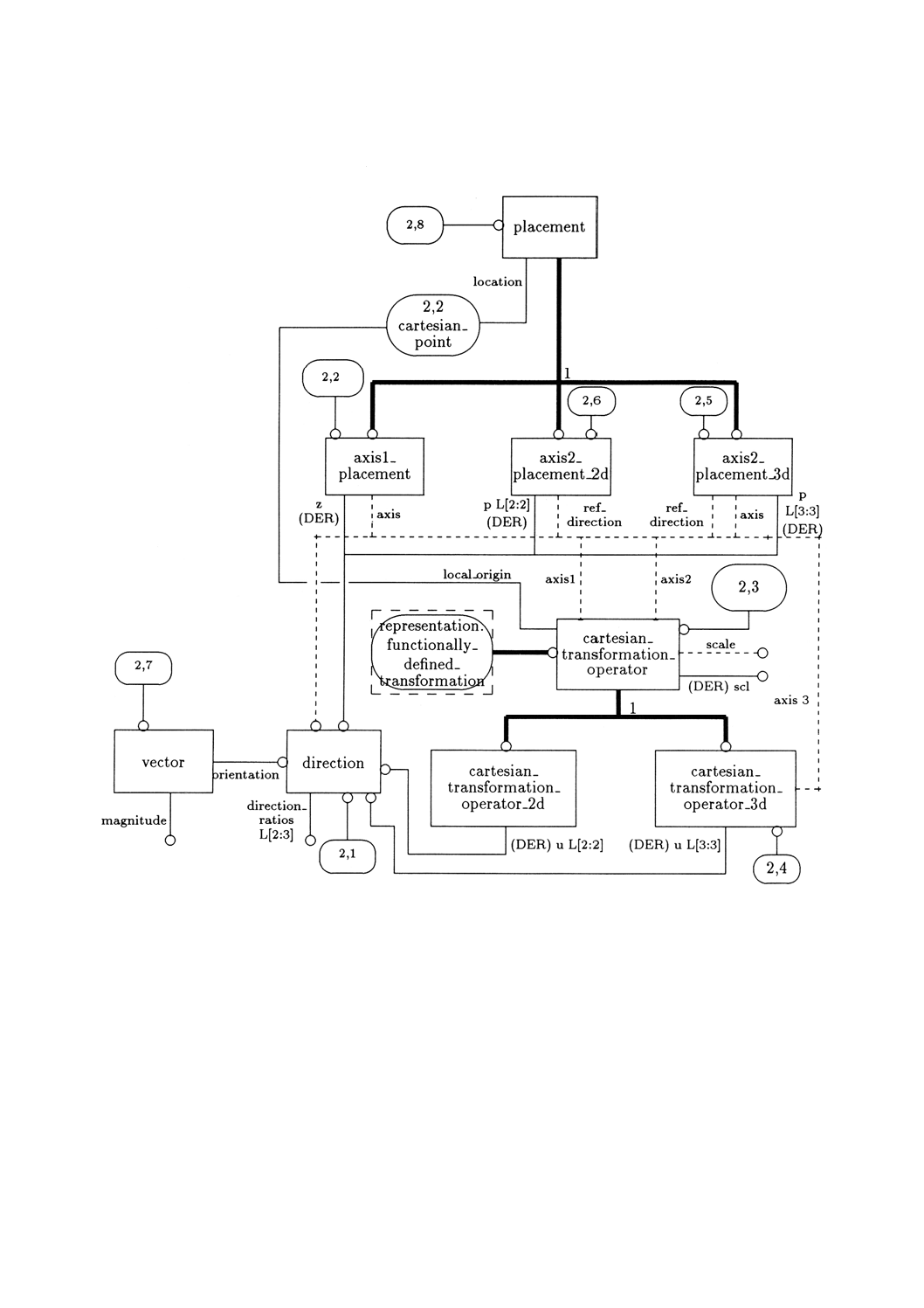
172
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.2 geometry̲schemaのEXPRESS-Gによる図式表現(2/12)
−placement及びcartesian̲transformation̲operatorの下位型
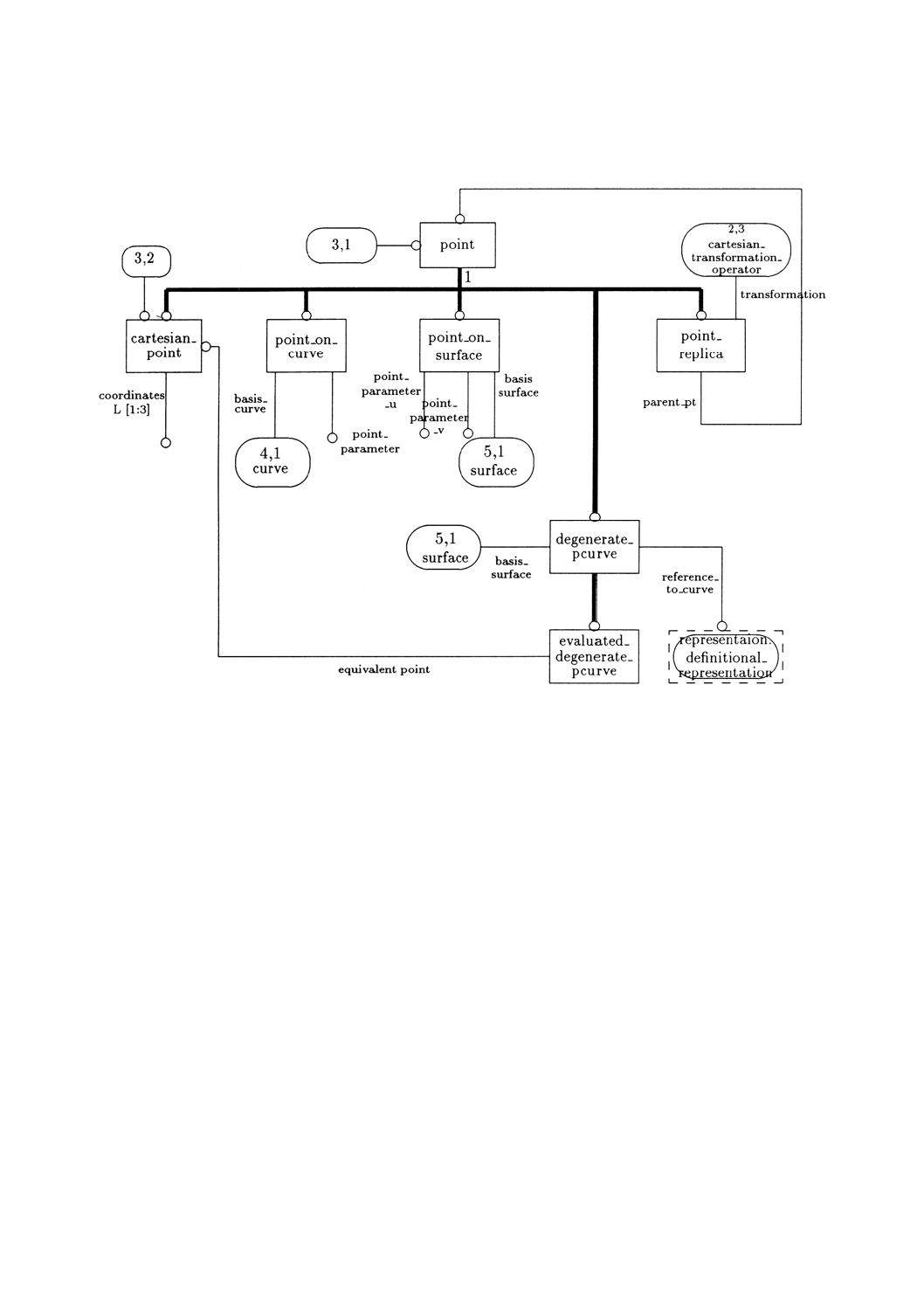
173
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.3 geometry̲schemaのEXPRESS-Gによる図式表現(3/12)
−pointの下位型
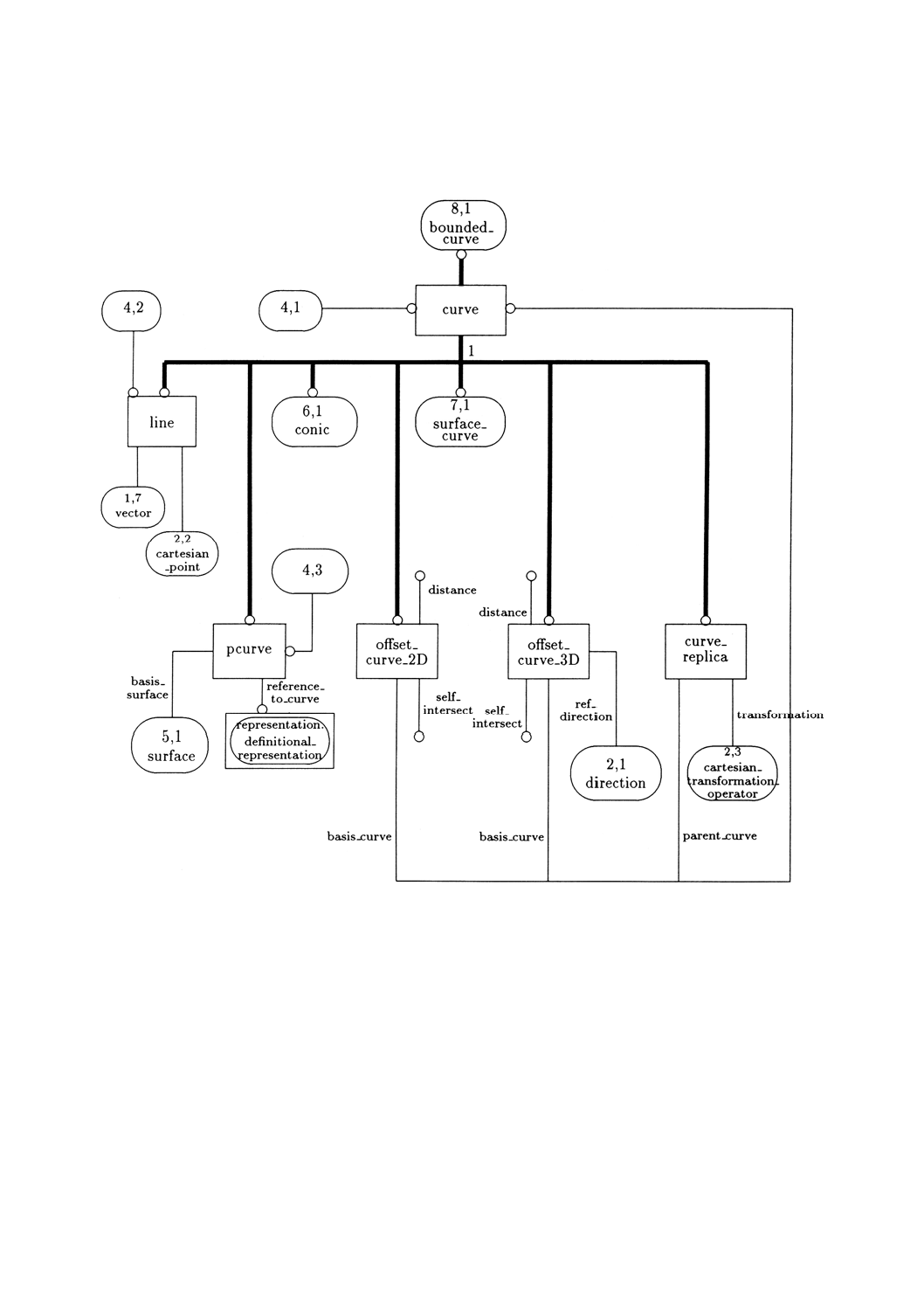
174
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.4 geometry̲schemaのEXPRESS-Gによる図式表現(4/12)
−curveの下位型
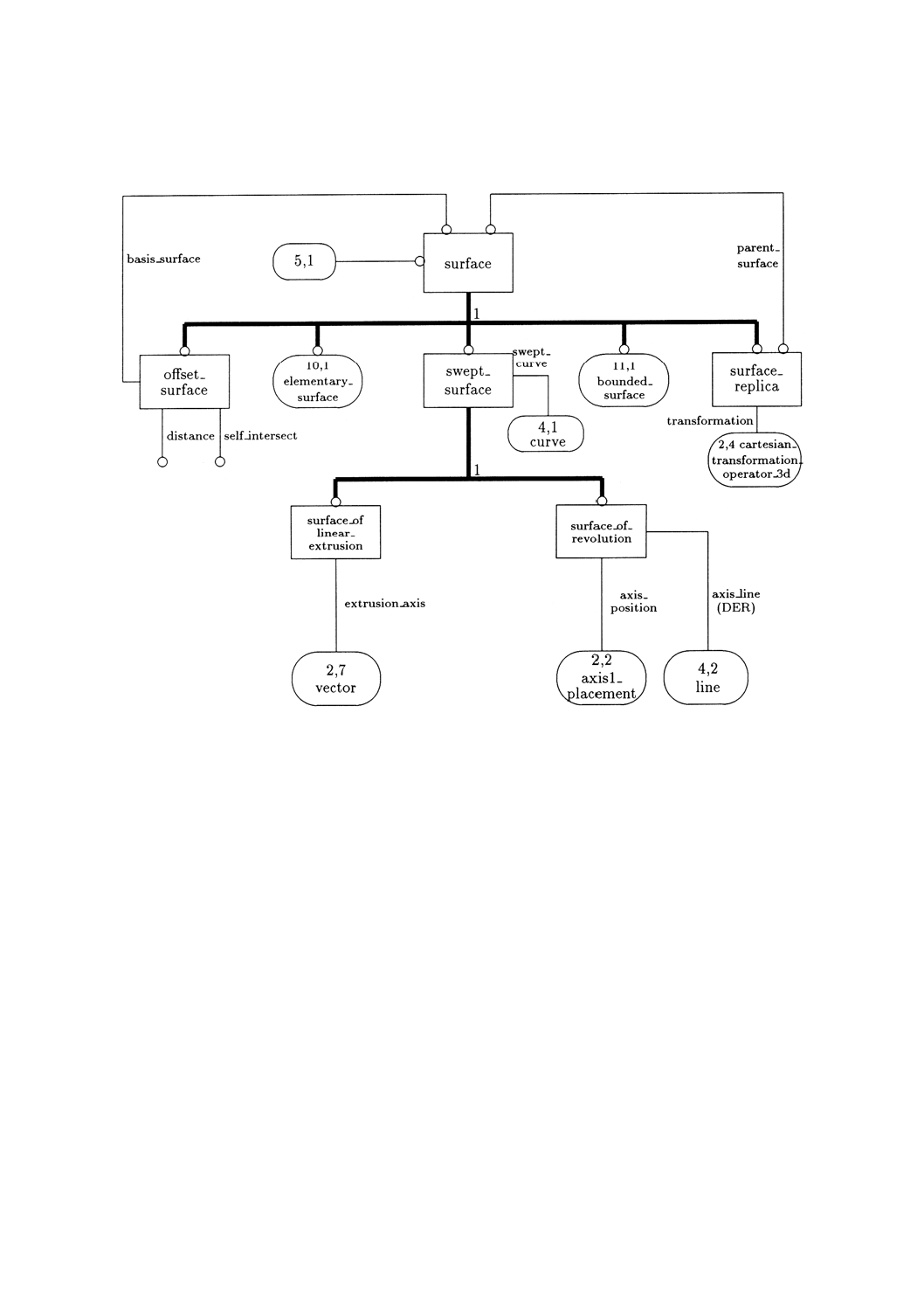
175
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.5 geometry̲schemaのEXPRESS-Gによる図式表現(5/12)
−surfaceの下位型
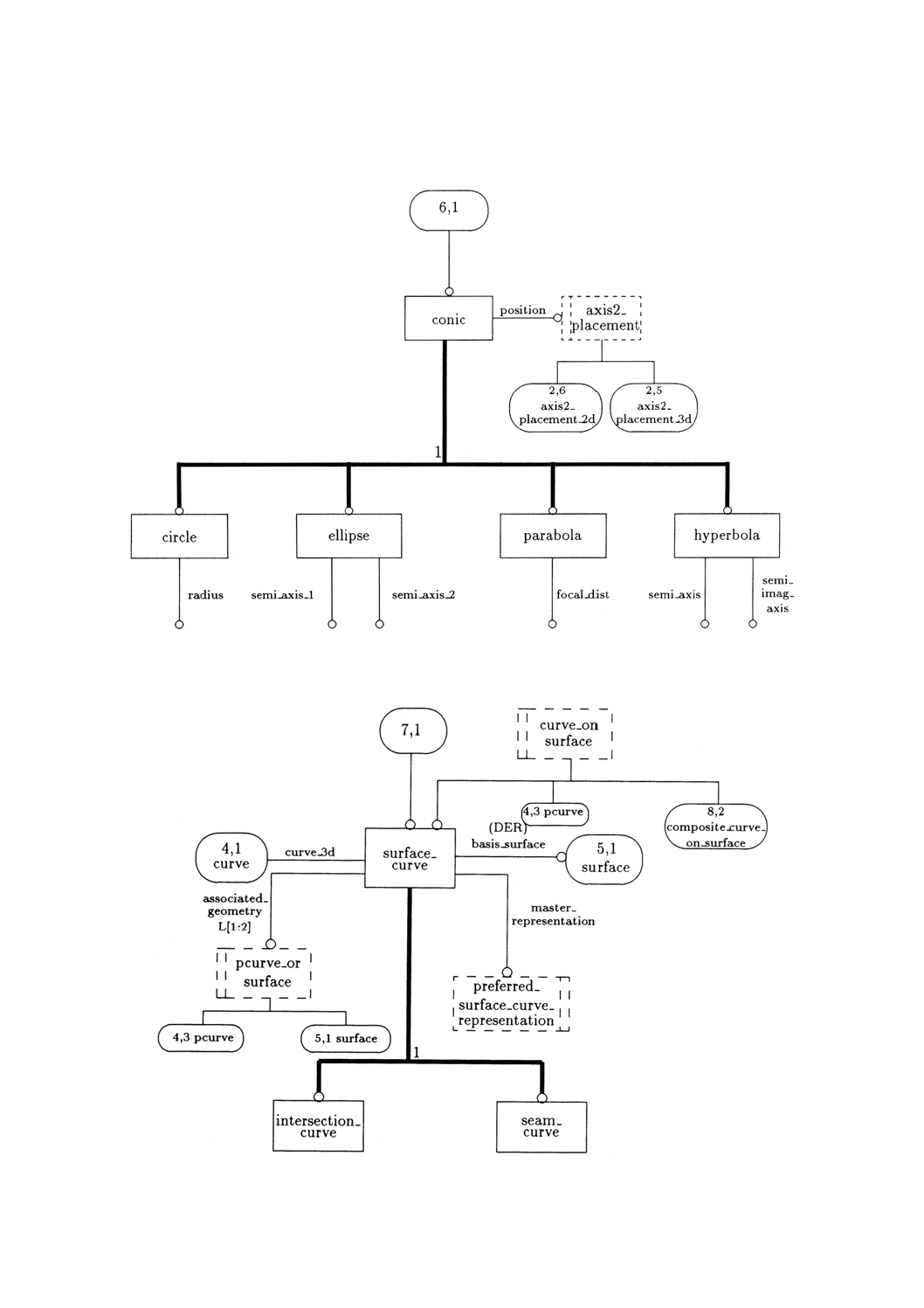
176
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.6 geometry̲schemaのEXPRESS-Gによる図式表現(6/12)
−conicの下位型
附属書D図D.7 geometry̲schemaのEXPRESS-Gによる図式表現(7/12)
−surface̲curveの下位型
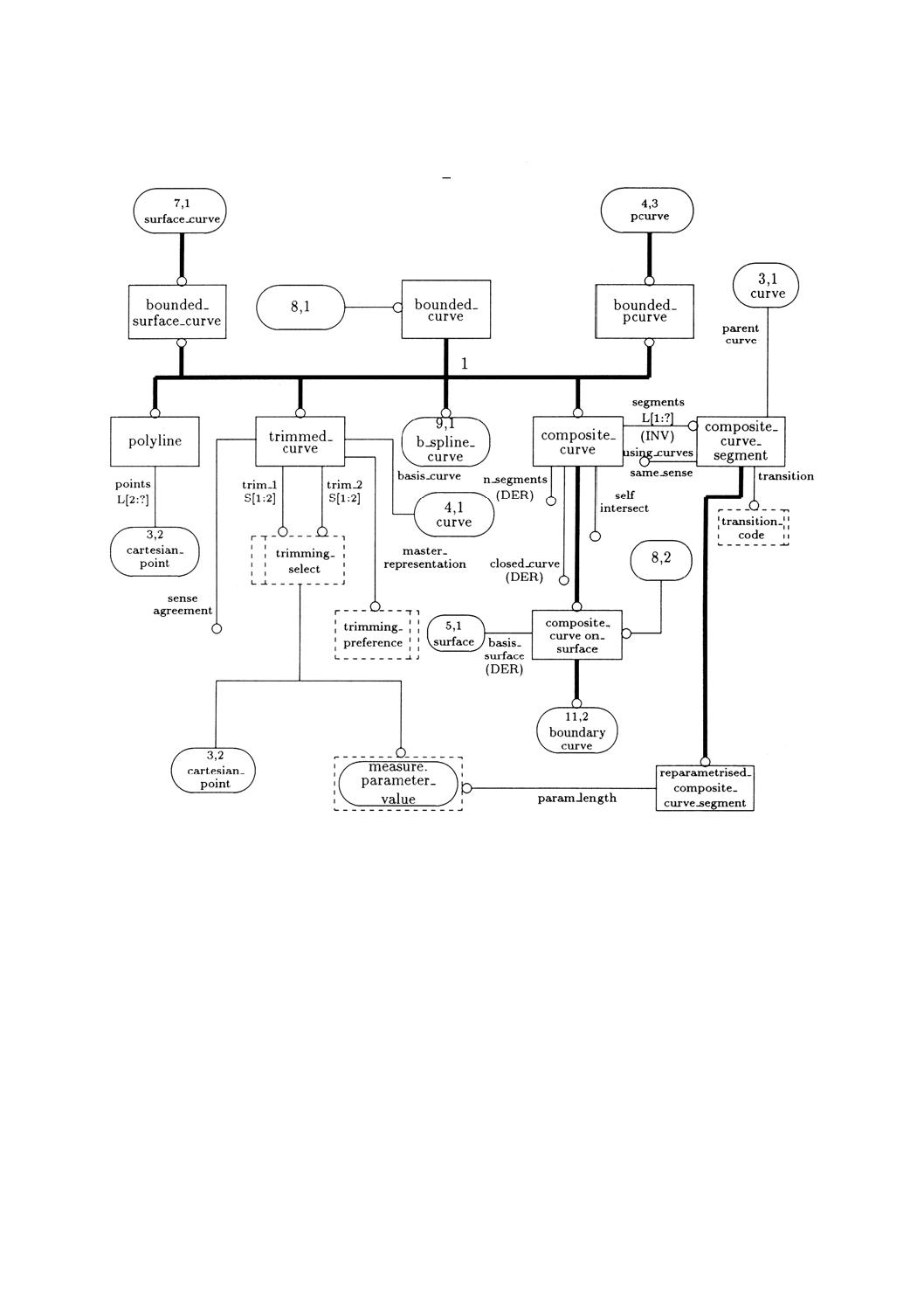
177
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.8 geometry̲schemaのEXPRIESS-Gによる図式表現(8/12)
−bounded̲curveの下位型
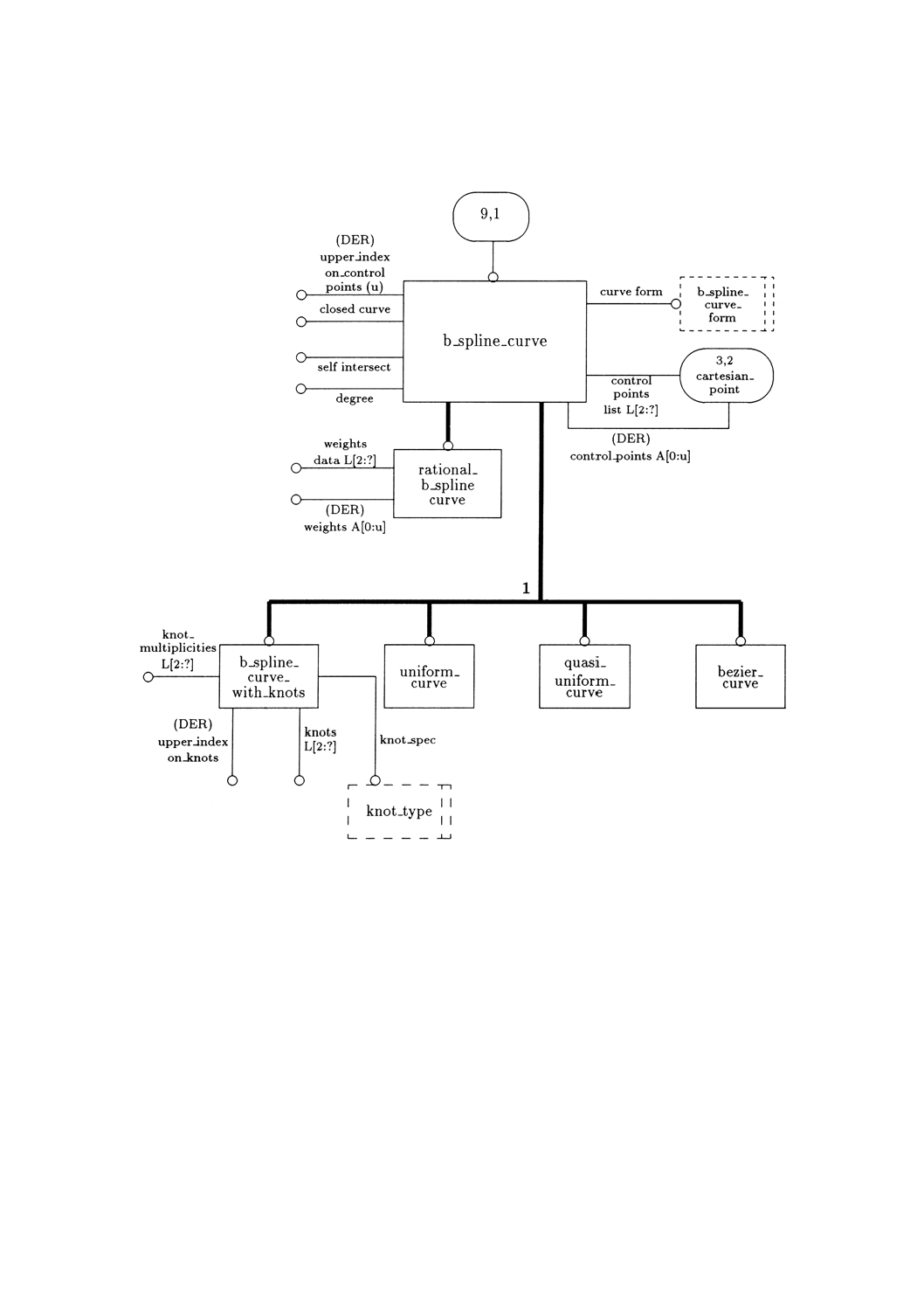
178
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.9 geometry̲schemaのEXPRESS-Gによる図式表現(9/12)
−b̲spline̲curveの下位型
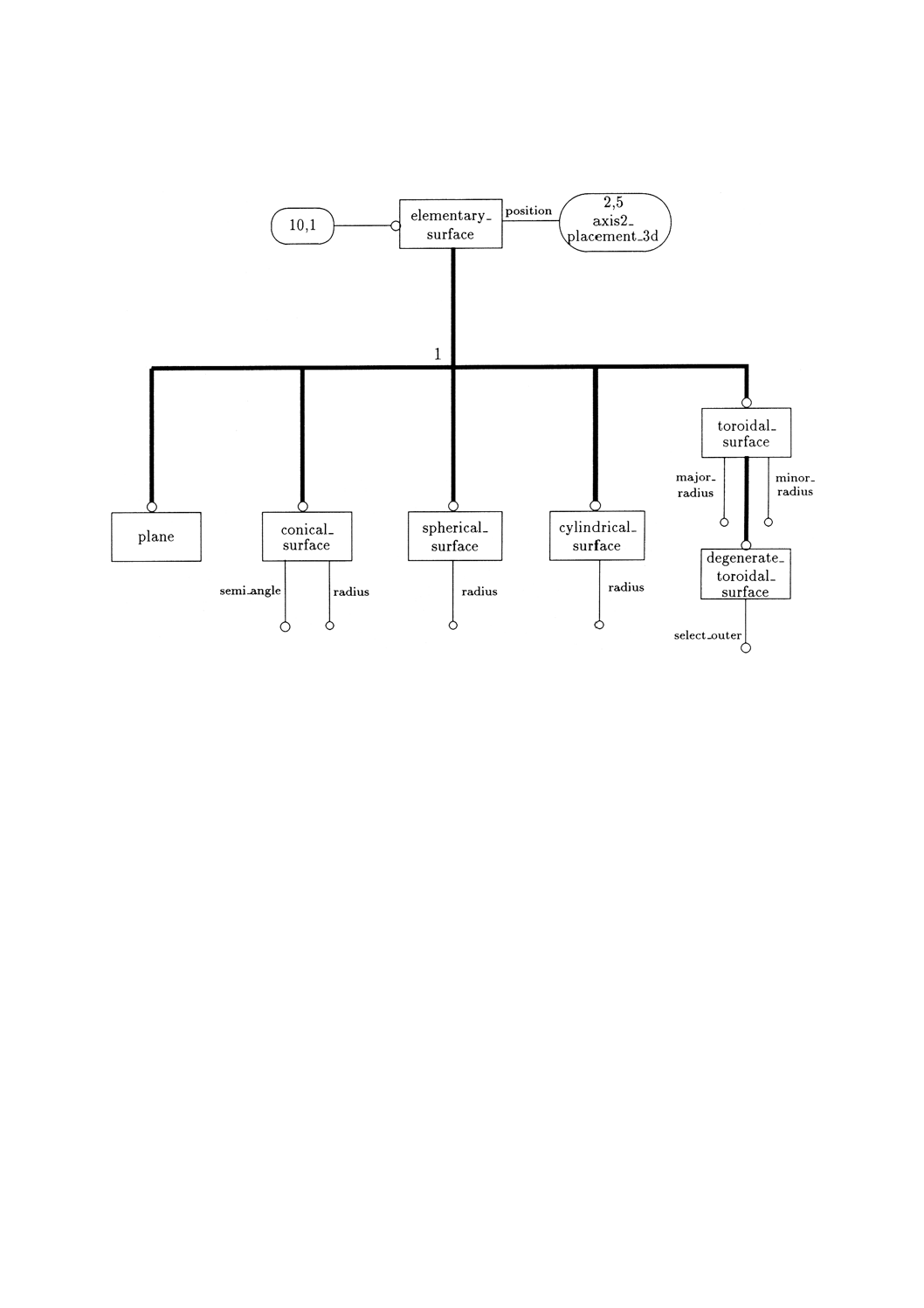
179
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.10 geometry̲schemaのEXPRESS-Gによる図式表現(10/12)
−elementary̲surfaceの下位型
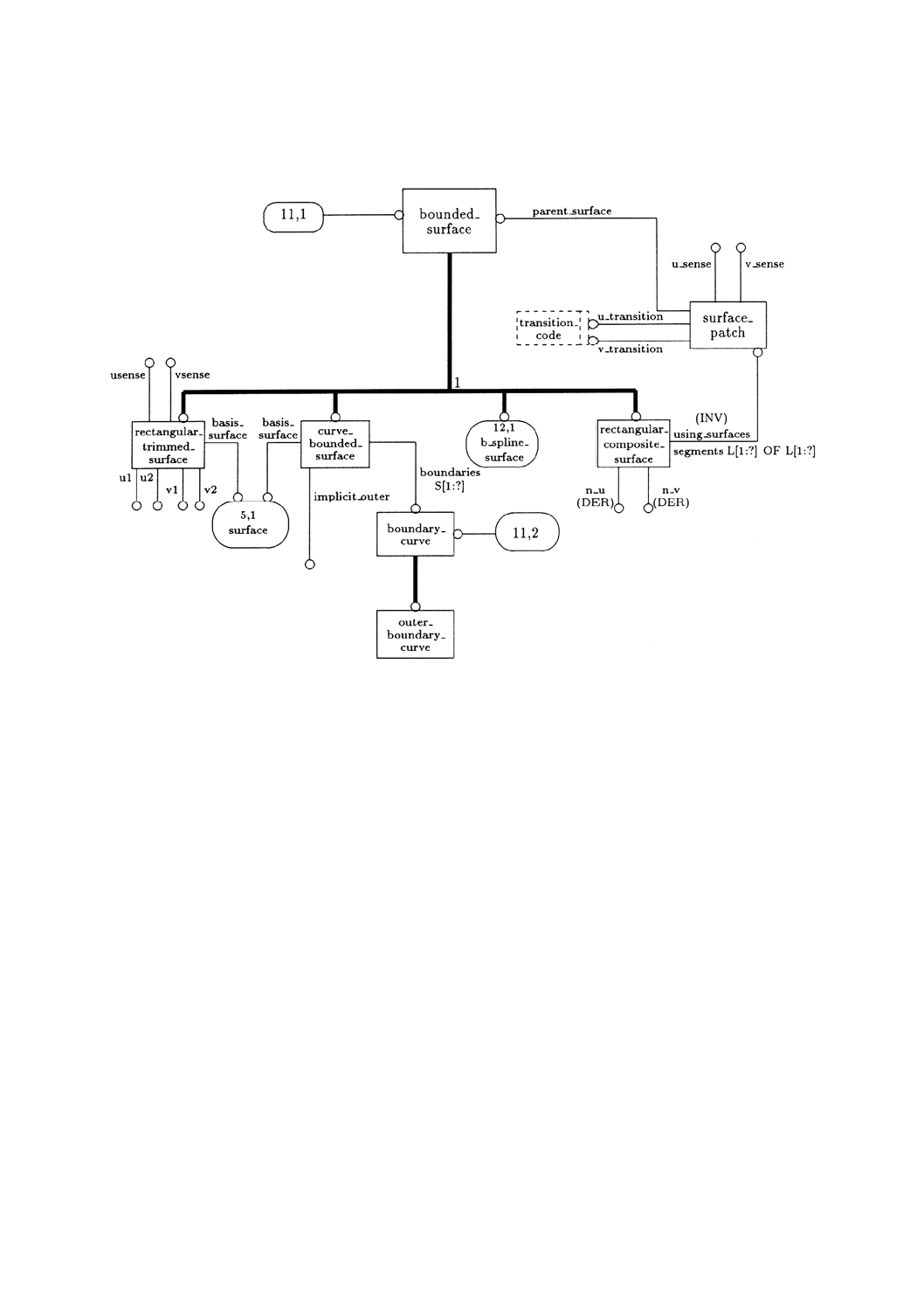
180
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.11 geometry̲schemaのEXPRESS-Gによる図式表現(11/12)
−bounded̲surfaceの下位型
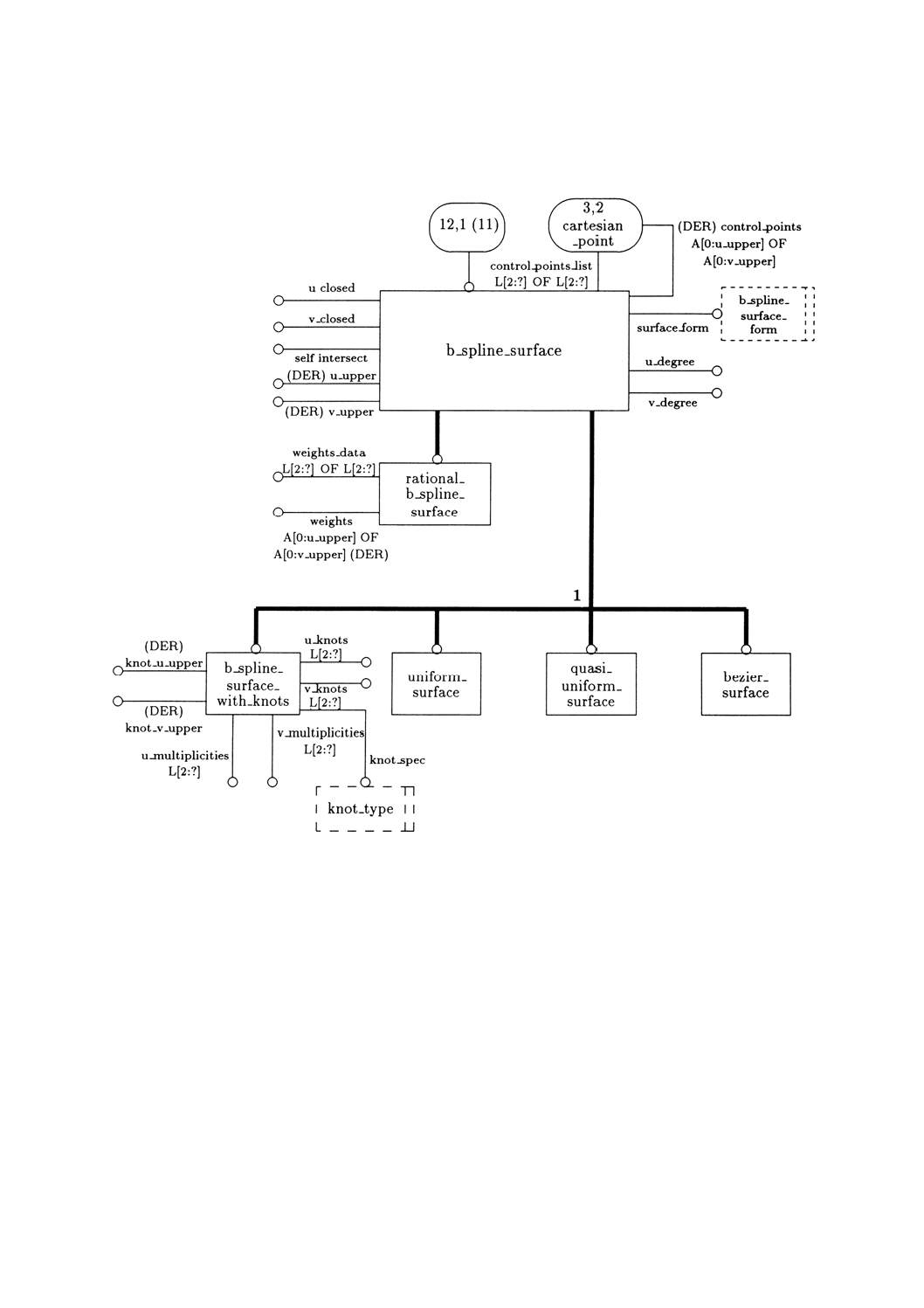
181
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.12 geometry̲schemaのEXPRIESS-Gによる図式表現(12/12)
−b̲spline̲surfaceの下位型
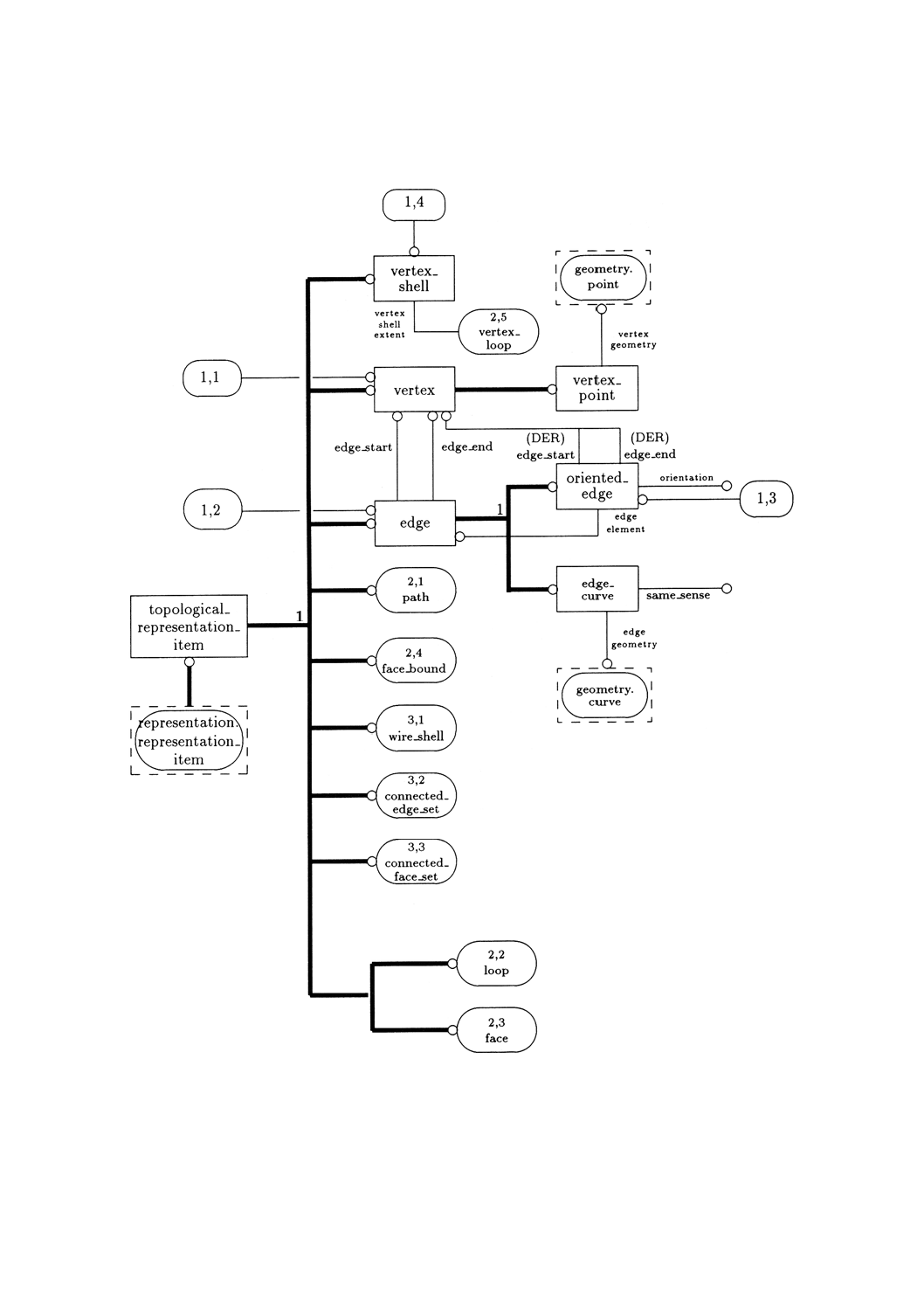
182
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.13 topology̲schemaのEXPRESS-Gによる図式表現(1/3)
−topological̲representation̲itemの下位型
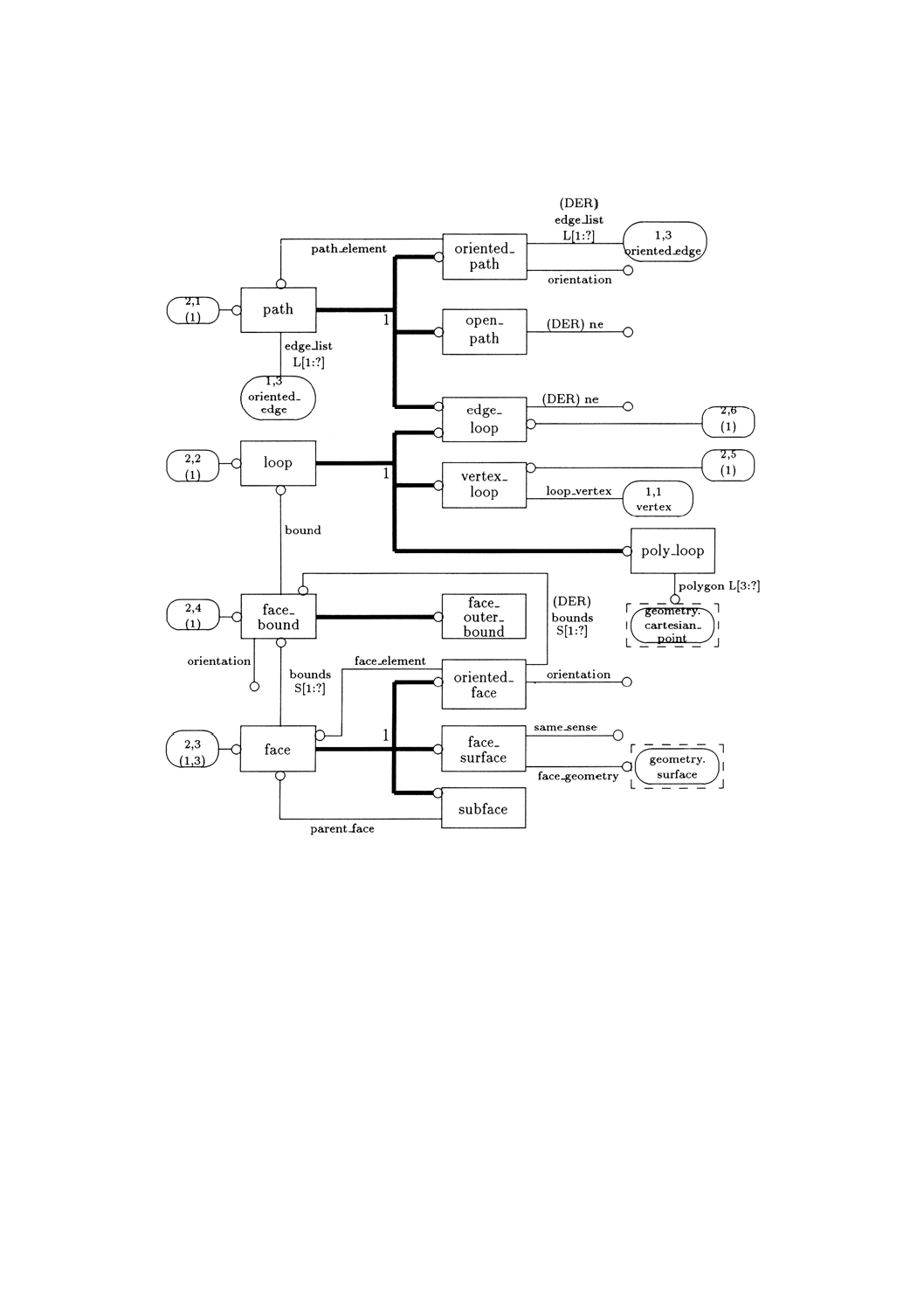
183
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.14 topology̲schemaのEXPRESS-Gによる図式表現(2/3)
−topological̲representation̲itemの下位型
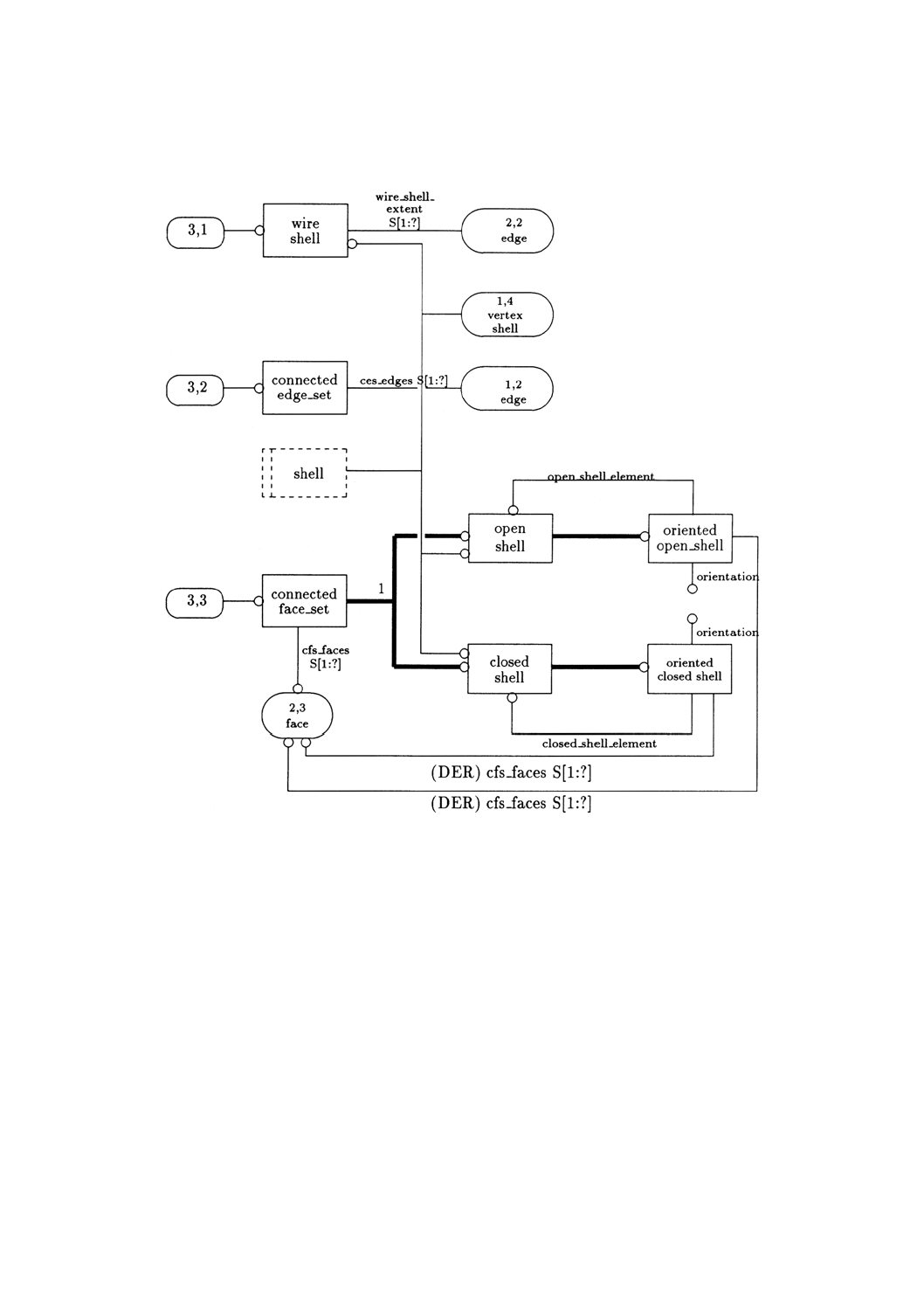
184
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.15 topology̲schemaのEXPRESS-Gによる図式表現(3/3)
−topological̲representation̲itemの下位型

185
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.16 geometric̲model̲schemaのEXPRESS-Gによる図式表現(1/3)
−solid̲modelの下位型
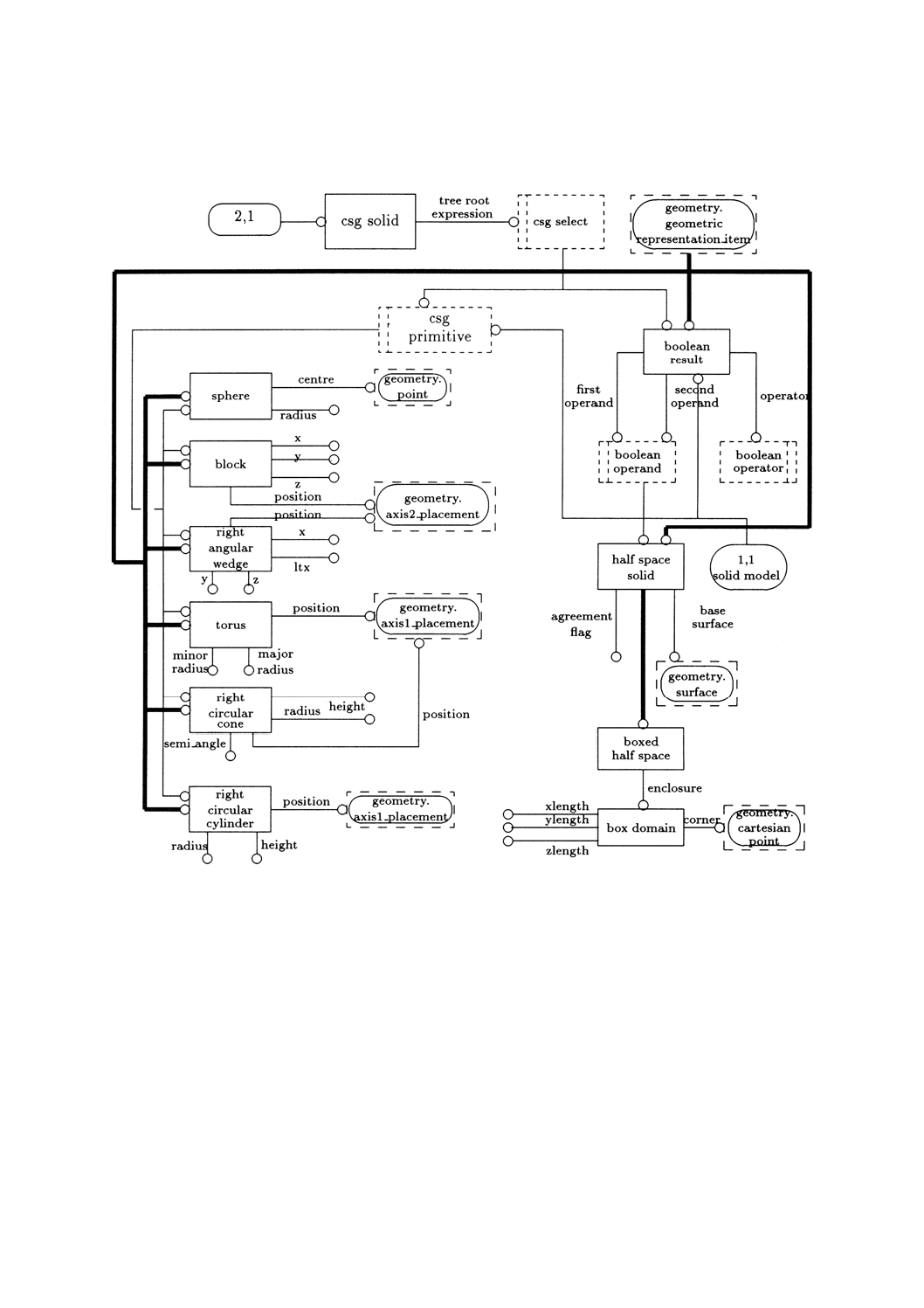
186
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.17 geometric̲model̲schemaのEXPRESS-Gによる図式表現(2/3)
−csg̲solid
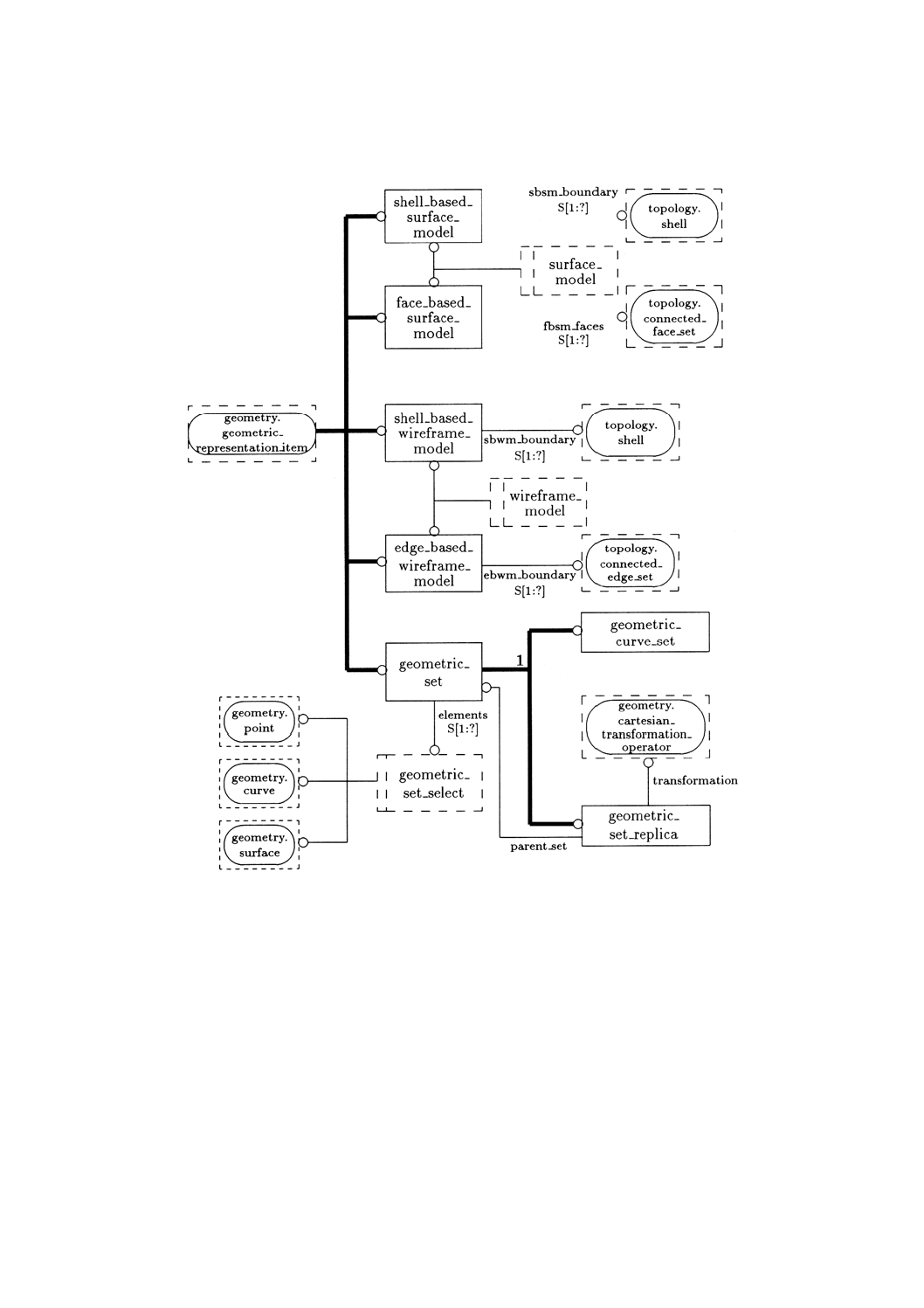
187
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D図D.18 geometric̲model̲schemaのEXPRESS-Gによる図式表現(3/3)
−その他の形状モデル
188
B 3700-42:1996 (ISO 10303-42:1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E(参考) 参考文献
1. FARIN, G.;Curves and Surfaces for Computer Aided Geometric Design, Academic Press, 1988.
2. BARTELS, BEATTY and BARSKY;Splines in Computer Graphics and Geometric Mouelling, Morgan
Kaufman, 1987.
3. The Initial Graphics Exchange Specification (IGES) Version 5.1, US Product Data Association, 1991.
4. WILSON, P.R.;Euler Formulas and Geometric Modeling, IEEE Computer Graphics & Applications, Vol.5, No
8, pp. 24-36, August 1985.





































